Tìm giá trị nhỏ nhất của M= \(10x^2-2\text{x}y+y^2+1-6\text{x}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/
\(BC=\sqrt{AB^2+AC^2}\) (Pitago)
\(\Rightarrow BC=\sqrt{6^2+8^2}=10cm\)
\(IB=IC\Rightarrow AI=\dfrac{BC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\Rightarrow AI=\dfrac{BC}{2}=\dfrac{10}{2}=5cm\)
b/
Ta có
OA=OC (gt)
OI=ON (gt)
=> AICN là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường) (1)
\(AI=IC=\dfrac{BC}{2}\) (2)
Từ (1) và (2)
=> AICN là hình thoi (Hình bình hành có hai cạnh liền kề bằng nhau)
Không đủ dữ kiện để c/m AICN là HCN

`c, ab <=(a+b)^2/4`.
Tương tự, `{(bc <=(b+c)^2/4), (ca<=(c+a)^2/4):}`
`-> ab/(a+b) + bc/(b+c) + ca/(c+a) <=(a+b+b+c+c+a)/4 = (a+b+c)/2`.
`d,` Đặt `b+c=x, c+a=y, a+b = z`, ta có:
`(-x+y+z)/2x + (-y+z+x)/2y + (-z+x+y)/2z = y/2x + z/2x + z/2y + x/2y + x/2z + y/2x >= 3/2.`
Đến đây bạn dùng BĐT Svac xơ nhé.

Lời giải:
$(x-5)(2-x)-(x-1)^2=(2x-x^2-10+5x)-(x^2-2x+1)$
$=7x-x^2-10-x^2+2x-1=(7x+2x)-(x^2+x^2)-(10+1)=9x-2x^2-11$

Lời giải:
$2a^2-bc^2-a^2b+2c^2=(2a^2+2c^2)-(bc^2+a^2b)$
$=2(a^2+c^2)-b(a^2+c^2)=(a^2+c^2)(2-b)$


`a)15x^{3}-x=0`
`=>x(15x^{2}-1)=0`
`=>x=0` hoặc `15x^{2}-1=0`
`=>x=0` hoặc \(x^2=\dfrac{1}{15}\)
`=>x=0` hoặc \(x=\pm\dfrac{1}{\sqrt{15}}=\pm\dfrac{\sqrt{15}}{15}\)
`b)(3x-2).(x+3)+(x^{2}-9)=0`
`=>(3x-2).(x+3)+(x-3)(x+3)=0`
`=>(x+3)(3x-2+x-3)=0`
`=>x+3=0` hoặc `4x-5=0`
`=>x=-3` hoặc `x=5/4`
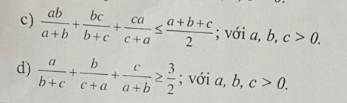
\(M=\left(x^2-2xy+y^2\right)+\left(9x^2-6x+1\right)=\left(x-y\right)^2+\left(3x-1\right)^2\ge0\)
\(M_{min}=0\) khi \(x=y=\dfrac{1}{3}\)