(0,5 điểm) Với các số thực $a$ và $b$ thỏa mãn $a^{2}+b^{2}=2$, tìm giá trị nhỏ nhất của biểu thức $P=3(a+b)+a b$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hoành độ giao điểm (P) ; (d) tm pt
\(x^2-2x-m+2=0\)
\(\Delta'=1-\left(-m+2\right)=m+3\)
Để (P) cắt (d) tại 2 điểm pb khi m > -3
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m+2\end{matrix}\right.\)
Ta có \(\left(x_1-x_2\right)^2=4\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4\)
Thay vào ta được \(4+4\left(m-2\right)=4\Leftrightarrow4m-4=4\Leftrightarrow m=2\)(tm)
\(\left\{{}\begin{matrix}\dfrac{9}{x+1}-6y=-3\\\dfrac{10}{x+1}+6y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{19}{x+1}=-19\\y=\dfrac{\dfrac{3}{x+1}+1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-1\end{matrix}\right.\)

1, Gọi số bộ đồ tổ sản xuất phải làm mỗi ngày theo kế hoạch là x ( x ϵ N* )
Gọi số bộ đồ tổ sản xuất làm được mỗi ngày theo thực tế là x + 100 ( bộ )
Thời gian tổ sản xuất làm theo kế hoạch là \(\dfrac{4800}{x}\)( ngày ) (1)
Thời gian tổ sản xuất làm thực tế là \(\dfrac{4800}{x+100}\)( ngày ) (2)
Thực tế, tổ sản xuất đã hoàn thành trước 8 ngày nên từ (1) và (2), ta có phương trình:
\(\dfrac{4800}{x}-\dfrac{4800}{x+100}=8\)
Sau đó giải như bth là xong ^^
2) Diện tích bề mặt hình trụ là:
2πrh = 2.3,14.0,5.1,6 ≈ 5,024 ( m2 )
Vậy diện tích bề mặt được sơn của thùng nước là 5,024 m2

1, Thay x = 16 vào ta được \(A=\dfrac{4}{4+3}=\dfrac{4}{7}\)
2, \(A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{-x+6\sqrt{x}-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}+3}\)
Ta có đpcm

\(P=\sqrt{a+b}+\sqrt{b+c}\sqrt{c+a}\)
Aps dụng Bunhia-cốpxki : \(P^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)\le\left(1+1+1\right)\left(a+b+b+c+c+a\right)\)
\(=6\left(a+b+c\right)\)
\(=6.2021=12126\Leftrightarrow P=\sqrt{12126}\)
Vậy \(Max\left(P\right)=\sqrt{12126}\Leftrightarrow a=b=c=\dfrac{2021}{3}\)
(Refer ;-;)

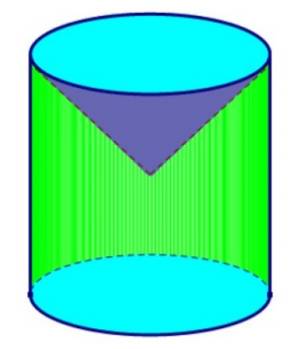
Thể tích của phần còn lại bằng thể tích của hình trụ tròn trừ đi thể tích của phần hình nón tiện.
V(hình trụ) = πr²h =π10²20= 2000π
V(nón) = 1/3 . πr²h(nón) =1/3 .π10². 10
V(cần tính) = V(hình trụ) - V(nón)
=2000π - 1000π/3
=5000π /3 (cm3)
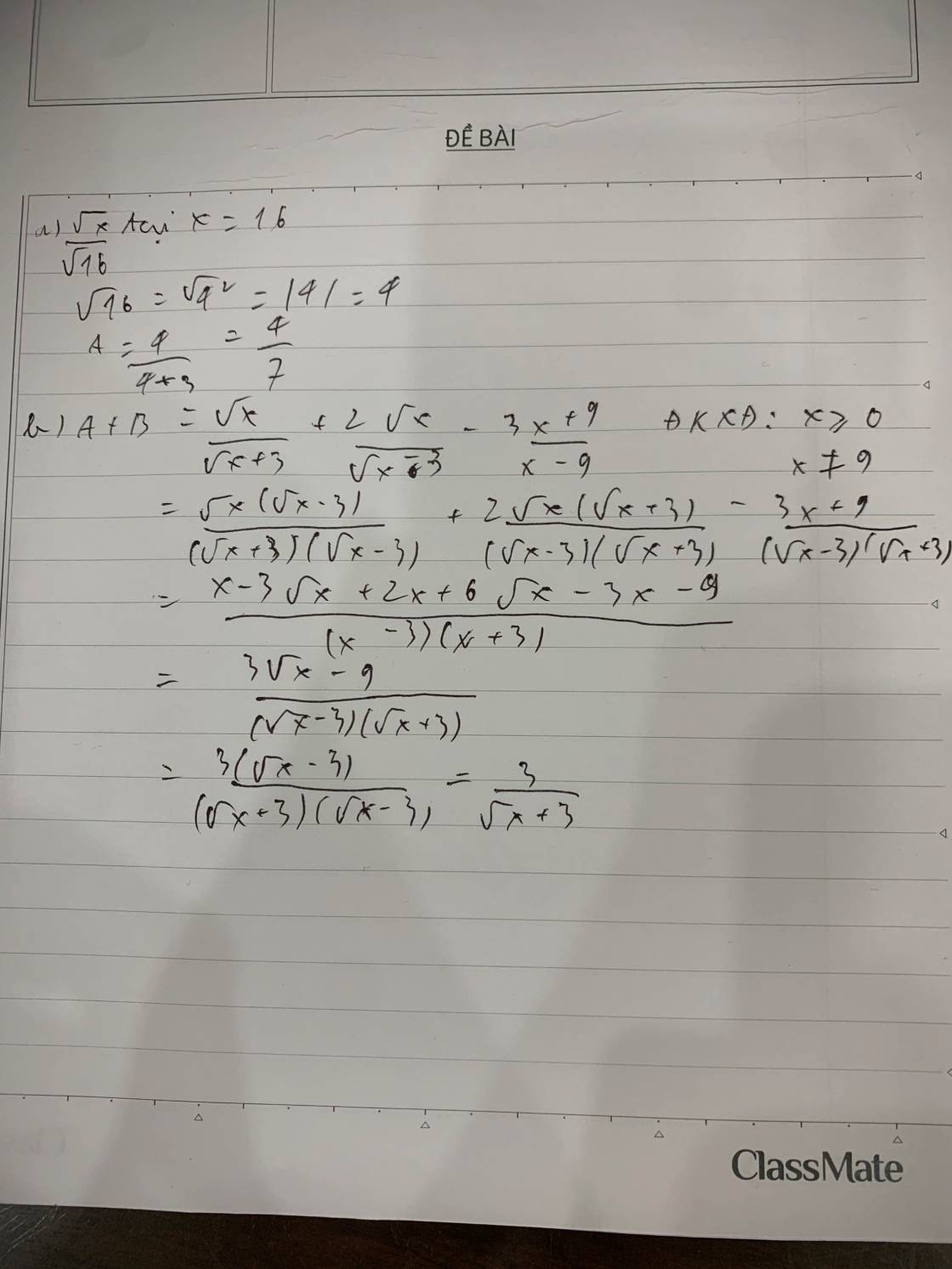
Từ điều kiện �2+�2=2a2+b2=2, ta có (�+�)2−2��=2⇒��=12(�+�)2−1(a+b)2−2ab=2⇒ab=21(a+b)2−1.
Đặt �=�+�x=a+b.
Khi đó �=3�+12�2−1=12(�+3)2−112P=3x+21x2−1=21(x+3)2−211.
Ta có (�+�)2≤2(�2+�2)⇒�2≤4⇒−2≤�≤2(a+b)2≤2(a2+b2)⇒x2≤4⇒−2≤x≤2.
Do đó �+3≥1⇒(�+3)2≥1⇒�≥−5x+3≥1⇒(x+3)2≥1⇒P≥−5.
Dấu bằng xảy ra khi �=�=−1a=b=−1.
Vậy giá trị nhỏ nhất của �P là −5−5.