Chứng tỏ B= 3 + 3 mũ 2 + 3 mũ 3+ 3 mũ 4+...........+ 3 mũ 2010chia hết cho 4 và 13 mình cần gắp lắm giải hộ mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

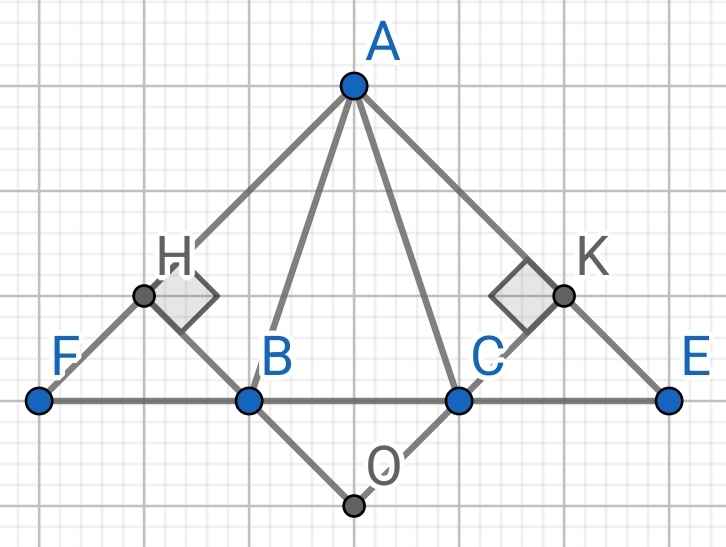
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB
Ta có:
∠ABF + ∠ABC = 180⁰ (kề bù)
∠ACE + ∠ACB = 180⁰ (kề bù)
Mà ∠ABC = ∠ACB (cmt)
⇒ ∠ABF = ∠ACE
Xét ∆ABF và ∆ACE có:
AB = AC (cmt)
∠ABE = ∠ACF (cmt)
BF = CE (gt)
⇒ ∆ABF = ∆ACE (c-g-c)
⇒ AF = AE (hai cạnh tương ứng)
⇒ ∆AEF cân tại A
b) *) Cách 1:
Do ∆ABF = ∆ACE (cmt)
⇒ ∠BAF = ∠CAE (hai góc tương ứng)
⇒ ∠BAH = ∠CAK
Xét hai tam giác vuông: ∆ABH và ∆ACK có:
AB = AC (cmt)
∠BAH = ∠CAK (cmt)
⇒ ∆ABH = ∆ACK (cạnh huyền - góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
*) Cách 2:
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF
⇒ ∠HFB = ∠KEC
Xét hai tam giác vuông: ∆BHF và ∆CKE có:
BF = CE (gt)
∠HFB = ∠KEC (cmt)
⇒ ∆BHF = ∆CKE (cạnh huyền - góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
c) Sửa đề: Gọi O là giao điểm của HB và KC
Do ∆BHF = ∆CKE (cmt)
⇒ ∠HBF = ∠KCE (hai góc tương ứng)
Mà ∠CBO = ∠HBF (đối đỉnh)
∠BCO = ∠KCE (đối đỉnh)
⇒ ∠CBO = ∠BCO
⇒ ∆BOC cân tại O

`#3107.101107`
\(106-\left(x+7\right)=9\\ \Rightarrow x+7=106-9\\ \Rightarrow x+7=97\\ \Rightarrow x=97-7\\ \Rightarrow x=90\)
Vậy, `x = 90`
___
\(45-\left(x+10\right)=31\\ \Rightarrow x+10=45-31\\ \Rightarrow x+10=14\\ \Rightarrow x=14-10\\ \Rightarrow x=4\)
Vậy, `x = 4`
___
\(156-\left(x+61\right)=82\\ \Rightarrow x+61=156-82\\ \Rightarrow x+61=74\\ \Rightarrow x=74-61\\ \Rightarrow x=13\)
Vậy, `x = 13`
___
\(126-\left(x+32\right)=86\\ \Rightarrow x+32=126-86\\ \Rightarrow x+32=40\\ \Rightarrow x=40-32\\ \Rightarrow x=8\)
Vậy, `x = 8.`

`#3107.101107`
`a)`
\(187+x=320\\ \Rightarrow x=320-187\\ \Rightarrow x=133\)
Vậy, `x = 133`
`b)`
\(765-x=158\\ \Rightarrow x=765-158\\ \Rightarrow x=607\)
Vậy, `x = 607`
`c)`
\(451+\left(x-218\right)=876\\ \Rightarrow x-218=876-451\\ \Rightarrow x-218=425\\ \Rightarrow x=425-218\\ \Rightarrow x=207\)
Vậy, `x = 207.`

a, \(1339:x=13\Leftrightarrow x=\dfrac{1339}{13}=103\)
b, \(1428:x=14\Leftrightarrow x=\dfrac{1428}{14}=102\)
c, \(2436:x=12\Leftrightarrow x=\dfrac{2436}{12}=203\)
a) 1339 : x = 13
x = 1339 : 13
x = 103
b) 1428 : x = 14
x = 1428 : 14
x = 102
c) 2436 : x = 12
x = 2436 : 12
x = 203

\(y=\dfrac{x^2-\left(x^2+4mx+1\right)}{x+\sqrt{x^2+4mx+1}}=\dfrac{-4mx-1}{x+\sqrt{x^2+4mx+1}}\)
\(=\dfrac{-4mx-1}{x+\left|x\right|\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}\)
\(\lim\limits_{x\rightarrow\pm\infty}y\dfrac{-4m-\dfrac{1}{x}}{1\pm\sqrt{1+\dfrac{4m}{x}+\dfrac{1}{x^2}}}=-4m\)
Để y = 1 là TCN => -4m = 1 => m = -1/4

\(\dfrac{x}{2}+\dfrac{x}{3}-1=\dfrac{1}{6}\Rightarrow3x+2x-6=1\Leftrightarrow5x=7\Leftrightarrow x=\dfrac{7}{5}\)

 -> Công thức tính số số hạng của dãy số cách đều tăng dần:
-> Công thức tính số số hạng của dãy số cách đều tăng dần:
(Số cuối - Số đầu) : Khoảng cách + 1
-> Công thức tính tổng dãy số cách đều với số hạng tăng dần:
(Số cuối + Số đầu) . Số số hạng : 2
a: 210:x-10=20
=>210:x=20+10=30
=>\(x=\dfrac{210}{30}=7\)(nhận)
b: \(770:\left[\left(20x+10\right):5\right]=35\)
=>\(\left(20x+10\right):5=\dfrac{770}{35}=22\)
=>20x+10=110
=>20x=100
=>x=5(nhận)
c: \(30-\left[4\left(x-2\right)+15\right]=3\)
=>4(x-2)+15=30-3=27
=>4(x-2)=27-15=12
=>x-2=3
=>x=3+2=5(nhận)
d: \(1+2+3+...+x=820\)
=>\(\dfrac{x\left(x+1\right)}{2}=820\)
=>x(x+1)=1640
=>\(x^2+x-1640=0\)
=>(x+41)(x-40)=0
=>\(\left[{}\begin{matrix}x=-41\left(loại\right)\\x=40\left(nhận\right)\end{matrix}\right.\)
e: (x-1)(x-3)=63
=>\(x^2-4x+3-63=0\)
=>\(x^2-4x-60=0\)
=>(x-10)(x+6)=0
=>\(\left[{}\begin{matrix}x=10\left(nhận\right)\\x=-6\left(loại\right)\end{matrix}\right.\)
f: \(\left(x+1\right)+\left(x+2\right)+...+\left(x+100\right)=5750\)
=>100x+(1+2+...+100)=5750
=>\(100x+100\cdot\dfrac{101}{2}=5750\)
=>100x+5050=5750
=>100x=700
=>x=7

`#3107.101107`
`a,`
\(12\cdot53+53\cdot172+184\cdot47\)
\(=53\cdot\left(12+172\right)+184\cdot47\\ =53\cdot184+184\cdot47\\ =184\cdot\left(53+47\right)\\ =184\cdot100\\ =18400\)
`b,`
\(43\cdot29+57\cdot29-73\cdot26-27\cdot26\\ =29\cdot\left(43+57\right)-26\cdot\left(73+27\right)\\ =29\cdot100-26\cdot100\\ =100\cdot\left(29-26\right)\\ =100\cdot3\\ =300\)
`c,`
\(4\cdot22\cdot87+11\cdot8\cdot36-2\cdot44\cdot23\\ =11\cdot4\cdot2\cdot87+11\cdot8\cdot36-11\cdot4\cdot2\cdot23\\ =11\cdot8\cdot87+11\cdot8\cdot36-11\cdot8\cdot23\\ =11\cdot8\cdot\left(87+36-23\right)\\ =88\cdot100\\ =8800\)
`d,`
\(100-96+92-88+84-80+...+12-8+4\)
Gọi tổng sau là A
`A = (100 - 96) + (92 - 88) + (84 - 80) + ... + (12 - 8) + 4`
Số số hạng có trong tổng A:
`(100 - 4) \div 4 + 1 = 25` (số hạng)
Ghép mỗi cặp 2 số lại với nhau, các cặp có trong tổng:
`25 \div 2 = 12` (dư 1 số)
Ta có:
`A = 4 + 4 + 4 + .... + 4 + 4`
Trong đó, có `12` cặp ghép với nhau (dư 1)
`A = 4 \times 12 + 4`
`= 48 + 4`
`= 52`
Vậy, tổng A có giá trị là `52.`
Số số hạng của B:
2010 - 1 + 1 = 2010 (số hạng)
Do 2010 ⋮ 2 và 2010 ⋮ 3 nên ta có thể nhóm các số hạng của B thành các nhóm có 2 số hạng và 3 số hạng như sau:
B = 3 + 3² + 3³ + 3⁴ + ... + 3²⁰¹⁰
= (3 + 3²) + (3³ + 3⁴) + ... + (3²⁰⁰⁹ + 3²⁰¹⁰)
= 3(1 + 3) + 3³(1 + 3) + ... + 3²⁰⁰⁹(1 + 3)
= 3.4 + 3³.4 + ... + 3²⁰⁰⁹.4
= 4.(3 + 3³ + ... + 3²⁰⁰⁹) ⋮ 4
B = 3 + 3² + 3³ + 3⁴ + ... + 3²⁰¹⁰
= (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) + ... + (3²⁰⁰⁸ + 3²⁰⁰⁹ + 3²⁰¹⁰)
= 3(1 + 3 + 3²) + 3⁴(1 + 3 + 3²) + ... + 3²⁰⁰⁸(1 + 3 + 3²)
= 3.13 + 3⁴.13 + ... + 3²⁰⁰⁸.13
= 13.(3 + 3⁴ + ... + 3²⁰⁰⁸) ⋮ 13
Vậy B ⋮ 4 và B ⋮ 13