4x2 - 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x-1}{x+2}+\dfrac{6x}{x^2-4}=\dfrac{x+1}{2-x}\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{x-1}{x+2}+\dfrac{6x}{\left(x-2\right)\left(x+2\right)}=-\dfrac{x+1}{x-2}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)+6x+\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\)
\(\Leftrightarrow x^2-2x-x+2+6x+x^2+2x+x+2=0\)
\(\Leftrightarrow2x^2+6x+4=0\)
\(\Leftrightarrow2x^2+2x+4x+4=0\)
\(\Leftrightarrow2x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x+4\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+4=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{-1\right\}\)


A B C D
\(\widehat{A}+\widehat{D}=70^o+110^o=180^o\)
=> ABCD là tứ giác nội tiếp (tứ giác có tổng 2 góc đối =180 là tứ giác nt)
\(\widehat{ABD}=\widehat{ACD}\) (góc nt cùng chắn cung AD) (1)
\(\widehat{CBD}=\widehat{CAD}\) (góc nt cùng chắn cung CD) (2)
Tg ADC cân tại D \(\Rightarrow\widehat{ACD}=\widehat{CAD}\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{ABD}=\widehat{CBD}\)

\(a,\left(x-2\right)\left(3x-1\right)=x\left(2-x\right)\)
\(\Leftrightarrow\left(x-2\right)\left(3x-1\right)+x\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(3x-1+x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy \(S=\left\{\dfrac{1}{4};2\right\}\)
\(b,\left|2x+3\right|=4x+1\)
\(TH_1:x\ge-\dfrac{3}{2}\)
\(2x+3=4x+1\\ \Leftrightarrow-2x=-2\\ \Leftrightarrow x=1\left(tm\right)\)
\(TH_2:x< -\dfrac{3}{2}\)
\(-2x-3=4x+1\\ \Leftrightarrow-6x=4\Leftrightarrow x=-\dfrac{2}{3}\left(ktm\right)\)
Vậy \(S=\left\{1\right\}\)
\(c,\dfrac{x+1}{3}+1=3-\dfrac{5x}{10}\\ \Leftrightarrow\dfrac{10\left(x+1\right)+30-90+15x}{30}=0\\ \Leftrightarrow10x+10-60+15x=0\\ \Leftrightarrow25x=50\\ \Leftrightarrow x=2\)
Vậy \(S=\left\{2\right\}\)
\(d,\dfrac{1}{x+2}+\dfrac{3}{2-x}=\dfrac{2x-3}{x^2-4}\left(dk:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{x-2-x-2-2x+3}{x^2-4}=0\)
\(\Leftrightarrow-2x=1\)
\(\Leftrightarrow x=-\dfrac{1}{2}\left(tmdk\right)\)
Vậy \(S=\left\{-\dfrac{1}{2}\right\}\)

\(a,\) P xác định \(\Leftrightarrow x^2-4\ne0\Leftrightarrow x\ne\pm2\)
\(b,P=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\dfrac{1}{x+2}\)
\(=\left(\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x-2}+\dfrac{1}{x+2}\right).\left(x+2\right)\)
\(=\dfrac{x-2\left(x+2\right)+x-2}{\left(x+2\right)\left(x-2\right)}.\left(x+2\right)\)
\(=\dfrac{x-2x-4+x-2}{x-2}\)
\(=\dfrac{-6}{x-2}\)

Bạn tự biểu diễn nha.
\(a,\dfrac{x-4}{6}+\dfrac{1}{2}>\dfrac{2x-5}{3}\)
\(\Leftrightarrow\dfrac{x-4}{6}+\dfrac{3}{6}-\dfrac{2\left(2x-5\right)}{6}>0\)
\(\Leftrightarrow\dfrac{x-4+3-4x+10}{6}>0\)
\(\Leftrightarrow-3x>-9\)
\(\Leftrightarrow x< 3\)
\(b,\dfrac{x+6}{5}-\dfrac{x-2}{3}< 2\)
\(\Leftrightarrow\dfrac{3\left(x+6\right)}{15}-\dfrac{5\left(x-2\right)}{15}-\dfrac{2.15}{15}< 0\)
\(\Leftrightarrow\dfrac{3x+18-5x+10-30}{15}< 0\)
\(\Leftrightarrow-2x< 2\)
\(\Leftrightarrow x>-1\)
\(c,x-\dfrac{x-1}{3}+\dfrac{x+2}{6}>\dfrac{2x}{5}+5\)
\(\Leftrightarrow\dfrac{30x-10\left(x-1\right)+5\left(x+2\right)-2x.6-5.30}{30}>0\)
\(\Leftrightarrow30x-10x+10+5x+10-12x-150>0\)
\(\Leftrightarrow13x>130\)
\(\Leftrightarrow x>10\)

Bạn cần phần nào thì mình sẽ giúp đỡ . Chứ bạn nhắn nhiều bài mình không giải được á . Chứ còn dạng bài như này thì hầu hết bạn đều phải nhân bung ra rồi rút gọn đi á .
muốn rối cái não bạn nhắn một lượt mình đọc không hiểu bạn nhắn từng câu thôi

Bài 1 :
Cách 1 : Dùng hằng đẳng thức : \(A^3-B^3=\left(A-B\right)\left(A^2+AB+B^2\right)\)
Áp dụng hằng đẳng thức trên ta suy ra được : đpcm.
Cách 2 :
\(VT=\left(x-1\right)\left(x^2+x+1\right)\)
\(=x^3+x^2+x-x^2-x-1\)
\(=x^3-1\left(VP\right)\)
suy ra : đpcm.
Bài 2 :
Hình như sai đề rồi á bạn . Đáp án đúng phải là \(x^4-y^4\) á cậu.
Cách 1 : Ta biến đổi vế phải thành vế trái .
Ta có : \(VP=x^4-y^4=\left(x^2+y^2\right)\left(x^2-y^2\right)\)
\(=\left(x^2+y^2\right)\left(x-y\right)\left(x+y\right)\)
\(=\left(x^3+x^2y+xy^2+y^3\right)\left(x-y\right)\left(VT\right)\)
Suy ra : đpcm.
Cách 2 : Bạn cũng có thể dùng hằng đẳng thức hoặc nhân bung vế trái ra á.

a) \(\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\left(ab+bc+ac\right)\)
\(=a^3+ab^2+ac^2+a^2b+b^3+c^2b+a^2c+b^2c+c^3-a^2b-abc-a^2c-ab^2-b^2c-abc-abc-bc^2-ac^2\)
\(=a^3+b^3+c^3-3abc\left(đpcm\right)\)
b) Bạn chỉ cần nhân bung cả 2 vế ra là được á .
c) \(2\left(a+b+c\right)\left(\dfrac{b}{2}+\dfrac{c}{2}-\dfrac{a}{2}\right)\)
\(=2\left(a+b+c\right)\left(\dfrac{b+c-a}{2}\right)\)
\(=\left(a+b+c\right)\left(b+c-a\right)\)
\(=ab+ac-a^2+b^2+bc-ab+bc+c^2-ac\)
\(=2bc+b^2+c^2-a^2\left(đpcm\right)\)
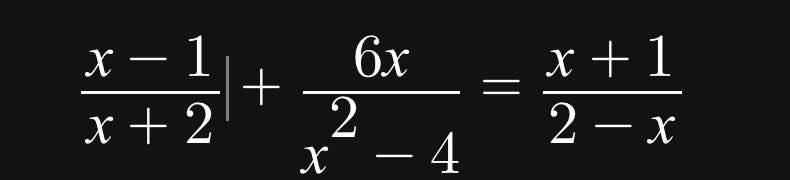



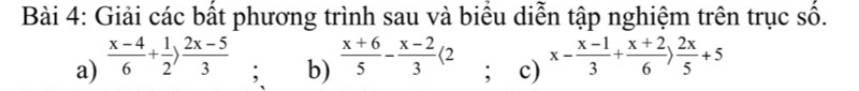
Đề yc gì em?