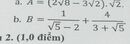Trục căn thức thôi bạn

\(B=\frac{1}{\sqrt{5}-2}+\frac{4}{3+\sqrt{5}}=\frac{\sqrt{5}+2}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}+\frac{4\left(3-\sqrt{5}\right)}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}\)

\(=\frac{\sqrt{5}+2}{5-4}+\frac{4\left(3-\sqrt{5}\right)}{9-5}\)

\(=\frac{\sqrt{5}+2}{1}+\frac{4\left(3-\sqrt{5}\right)}{4}\)

\(=\sqrt{5}+2+3-\sqrt{5}=5\)

Tương tự mấy phần kia 

\(A=\frac{x+3}{x-2}+\frac{x+2}{3-x}+\frac{x+2}{x^2-5x+6}\)

\(=\frac{x+3}{x-2}-\frac{x+2}{x-3}+\frac{x+2}{\left(x-2\right)\left(x-3\right)}\)

\(=\frac{\left(x+3\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}-\frac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}+\frac{x+2}{\left(x-2\right)\left(x-3\right)}\)

\(=\frac{x^2-9-x^2+4+x+2}{\left(x-2\right)\left(x-3\right)}=\frac{-3+x}{\left(x-2\right)\left(x-3\right)}=\frac{-1}{x-2}\)

mình hoàn thiện nốt bài bạn ở trên nhé

Do \(x^2+xu+u^2\)là một bình phương thiếu nên \(x^2+xu+u^2\ge0\Rightarrow x^2+xu+u^2+2\ge2>0\text{​​}\)

vậy hệ phương trình ban đầu \(\Leftrightarrow x=u\) hay \(x=\sqrt[3]{2x+1}\Leftrightarrow x^3=2x+1\Leftrightarrow\left(x+1\right)\left(x^2-x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1\pm\sqrt{5}}{2}\end{cases}}\)vậy pt có ba nghiệm 

Dat u=\(\sqrt[3]{2x-1}\)

ta co he \(\hept{\begin{cases}x^3+1=2u\\u^3+1=2x\end{cases}^{ }}\)(he nay doi xung )

tru ve vs ve ta co:

\(x^3-u^3=2\left(u-x\right)\)

\(\Leftrightarrow\left(x-u\right)\left(x^2+xu+u^2+2\right)=o\)

phan sau tu giai nha muon roi minh buon ngu 

\(\frac{1}{x-2}-\frac{1}{x+2}+\frac{4x-x^2}{4-x^2}\)

\(=\frac{x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x+2\right)\left(x-2\right)}+\frac{4x-x^2}{\left(2-x\right)\left(x+2\right)}\)

\(=\frac{x+2-x+2-4x+x^2}{\left(x+2\right)\left(x-2\right)}=\frac{-4x+4+x^2}{\left(x+2\right)\left(x-2\right)}\)

\(=\frac{\left(x-2\right)^2}{\left(x+2\right)\left(x-2\right)}=\frac{x-2}{x+2}\)

\(\frac{1}{x-2}-\frac{1}{x+2}+\frac{4x-x^2}{4-x^2}\)

\(=\frac{1}{x-2}-\frac{1}{x+2}+\frac{x^2-4x}{x^2-4}\)

\(=\frac{1}{x-2}-\frac{1}{x+2}+\frac{x^2-4x}{\left(x-2\right)\left(x+2\right)}\)

\(=\frac{x+2}{\left(x-2\right)\left(x+2\right)}-\frac{x-2}{\left(x-2\right)\left(x+2\right)}+\frac{x^2-4x}{\left(x-2\right)\left(x+2\right)}\)

\(=\frac{x+2-x+2+x^2-4x}{\left(x-2\right)\left(x+2\right)}\)

\(=\frac{x^2-4x+4}{\left(x-2\right)\left(x+2\right)}=\frac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\frac{x-2}{x+2}\)

\(\frac{2x^2-1}{x^2-xy}+\frac{1-2y^2}{x^2-xy}=\frac{2x^2-1+1-2y^2}{x^2-xy}\)

\(=\frac{2x^2-2y^2}{x^2-xy}=\frac{2\left(x^2-y^2\right)}{x\left(x-y\right)}\)

\(=\frac{2\left(x-y\right)\left(x+y\right)}{x\left(x-y\right)}=\frac{2\left(x+y\right)}{x}\)

Sửa đề : \(\frac{2x^2-1}{x^2-xy}+\frac{1-2y^2}{x^2-xy}\)

\(=\frac{2x^2-1+1-2y^2}{x^2-xy}=\frac{2x^2-2y^2}{x\left(x-y\right)}=\frac{2\left(x^2-y^2\right)}{x\left(x-y\right)}\)

\(=\frac{2\left(x-y\right)\left(x+y\right)}{x\left(x-y\right)}=\frac{2\left(x+y\right)}{x}\)

a, \(x^2-4x=0\Leftrightarrow x\left(x-4\right)=0\Leftrightarrow x=0;4\)

b, \(x^3+x^2-9x-9=0\Leftrightarrow x^2\left(x+1\right)-9\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-9\right)=0\Leftrightarrow\left(x+1\right)\left(x-3\right)\left(x+3\right)=0\Leftrightarrow x=-1;\pm3\)

c, \(x^2-3x-10=0\Leftrightarrow x^2+2x-5x-10=0\)

\(\Leftrightarrow\left(x-5\right)\left(x+2\right)=0\Leftrightarrow x=5;-2\)

a, \(20x^2y^3-15xy^2=5xy^2\left(4xy-3\right)\)

b, \(3x+3y-x^2-xy=3\left(x+y\right)-x\left(x+y\right)=\left(3-x\right)\left(x+y\right)\)

c, \(9-x^2-y^2+2xy=9-\left(x^2+y^2-2xy\right)\)

\(=3^2-\left(x-y\right)^2=\left(3-x+y\right)\left(3+x-y\right)\)

20x²y³ - 15xy² = 5xy²( 4xy - 3 )

3x + 3y - x² - xy = ( 3x + 3y ) - ( x² + xy ) = 3( x + y ) - x( x + y ) = ( x + y )( 3 - x )

9 - x² - y² + 2xy = 9 - ( x² - 2xy + y² ) = 3² - ( x - y )² = ( 3 - x + y )( 3 + x - y )