Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
c.
Từ câu a ta suy ra \(BD=CD\)
Xét hai tam giác vuông BDE và CDF có:
\(\left\{{}\begin{matrix}\widehat{B}=\widehat{C}\\BD=CD\end{matrix}\right.\) \(\Rightarrow\Delta_{\perp}BDE=\Delta_{\perp}CDF\left(ch-gn\right)\)
\(\Rightarrow BE=CF\)
Mà \(AB=AC\left(gt\right)\Rightarrow AE+BE=AF+CF\)
\(\Rightarrow AE=AF\) (1)
Theo cm câu b ta có \(DE=DF\) (2)
(1);(2) \(\Rightarrow AD\) là trung trực của EF
\(\Rightarrow AD\perp EF\)
\(\Rightarrow EF||BC\) (cùng vuông góc AD)
a.
Do \(DE||BC\Rightarrow\widehat{BDE}=\widehat{DBC}\) (so le trong)
Theo giả thiết BD là phân giác \(\Rightarrow\widehat{DBC}=\widehat{DBE}\)
\(\Rightarrow\widehat{BDE}=\widehat{DBE}\)
\(\Rightarrow\Delta EBD\) cân tại E
\(\Rightarrow BE=DE\)
Do BD là phân giác \(\Rightarrow\widehat{B}=2\widehat{DBC}\)
Mà \(\widehat{B}=2\widehat{C}\) (giả thiết)
\(\Rightarrow\widehat{DBC}=\widehat{C}\)
\(\Rightarrow\Delta DBC\) cân tại D
\(\Rightarrow BD=CD\)
b.
Giả sử \(AD=DC\Rightarrow D\) là trung điểm AC
\(\Rightarrow BD\) là đường trung tuyến ứng với AC
Mà \(BD\) cũng là phân giác (gt)
\(\Rightarrow BD\) vừa là trung tuyến vừa là phân giác kẻ từ đỉnh B
\(\Rightarrow\Delta ABC\) cân tại B
\(\Rightarrow\widehat{A}=\widehat{C}\)
Mà \(\widehat{B}=2\widehat{C}\Rightarrow\widehat{B}=\widehat{A}+\widehat{C}\)
\(\Rightarrow2\widehat{B}=\widehat{A}+\widehat{B}+\widehat{C}\)
Theo tính chất tổng 3 góc trong tam giác:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow2\widehat{B}=180^0\)
\(\Rightarrow\widehat{B}=90^0\)
\(\Rightarrow\Delta ABC\) vuông tại B
\(\Rightarrow\Delta ABC\) vuông cân tại B
Vậy để \(AD=DC=BD\) thì tam giác ABC vuông cân tại B
c.
Ta có: \(BM=MG\Rightarrow\Delta MBG\) vuông cân tại M
\(\Rightarrow\widehat{MBG}=\widehat{MGB}=45^0\)
\(\left\{{}\begin{matrix}MB=MC\\MB=MG\end{matrix}\right.\) \(\Rightarrow MC=MG\Rightarrow\Delta MGC\) vuông cân tại M
\(\Rightarrow\widehat{MCG}=\widehat{MGC}=45^0\)
Do \(AI\perp GI\Rightarrow\Delta AGI\) vuông tại I
\(\Rightarrow\widehat{GAI}+\widehat{AGI}=90^0\Rightarrow\widehat{GAI}+\widehat{MGC}=90^0\)
\(\Rightarrow\widehat{GAI}=90^0-\widehat{MGC}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{GAI}=\widehat{AGI}\)
\(\Rightarrow\Delta AGI\) vuông cân tại I
\(\Rightarrow GI=AI\) (1)
Trong tam giác vuông ACI vuông tại I, do AC là cạnh huyền là AI là cạnh góc vuông
\(\Rightarrow AC>AI\) (2)
(1);(2) \(\Rightarrow AC>GI\)
d.
Do \(AH||GI\left(gt\right)\), mà \(GI\perp GB\) (theo cm câu b)
\(\Rightarrow AH\perp GB\) tại H
\(\Rightarrow\Delta AHG\) vuông tại H
\(\Rightarrow\widehat{HAG}+\widehat{HGA}=90^0\Rightarrow\widehat{HAG}+\widehat{MGB}=90^0\)
\(\Rightarrow\widehat{HAG}+45^0=90^0\Rightarrow\widehat{HAG}=45^0\)
\(\Rightarrow\widehat{HAG}=\widehat{HGA}\Rightarrow\Delta HAG\) cân tại H
\(\Rightarrow HA=HG\) (3)
Từ (1); (3) \(\Rightarrow HI\) là trung trực của AG
\(\Rightarrow HI\perp AG\)
Theo giả thiết \(BC\perp AG\)
\(\Rightarrow HI||BC\)
Mn biết nè , đáp án là 500 đấy
Cậu ghi vào đi chắc chắn là đúng
Bạn biết tại sao mn biết ko
Tại vì mn đoán bừa mà
a) do tg abc cân tại A=> ab=ac;^b=^c
xét tg abm và tg acm có:
ab=ac
^b=^c
^amb=^amc=90
=>tg amb=tg amc(ch-gn)=>mb=mc=>m là trung điểm của bc
b) do mb=mg mà mb=mc=>mb=mg=mc
do mb=mg mà ^bmg=90=>tg bmg vuông cân tại M=>^mbg=^mgb=45
do mg=mc mà cmg=90=>tg mcg vuông cân tại M=> ^mcg=^mgc=45
mà ^bcg=^mgb+^mgc=45+45=90=>bg vuông góc gc
c)
a: Biến cố ngẫu nhiên là A,C
Biến cố chắc chắn là biến cố B
Không có biến cố nào là không thể
b: A: “Bạn Ngọc được chọn”.
=>n(A)=1
=>\(P\left(A\right)=\dfrac{1}{25}\)
C: “Bạn được chọn có số thứ tự lớn hơn số thứ tự của bạn Ngọc”.
=>C={16;17;...;25}
=>n(C)=25-16+1=10
=>\(P\left(C\right)=\dfrac{10}{25}=\dfrac{2}{5}\)
a: Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Xét ΔABC có \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
c: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAF=ΔDEC
=>DF=DC
mà DC>DE(ΔDEC vuông tại E)
nên DF>DE
(2): \(A\left(x\right)=x^2-4x+5\)
\(B\left(x\right)=-x^2+6x-7\)
a) \(A\left(x\right)+B\left(x\right)\)
\(=\left(x^2-4x+5\right)+\left(-x^2+6x-7\right)\)
\(=x^2-4x+5-x^2+6x-7\)
\(=2x-2\)
b) \(A\left(x\right)-B\left(x\right)\)
\(=\left(x^2-4x+5\right)-\left(-x^2+6x-7\right)\)
\(=x^2-4x+5+x^2-6x+7\)
\(=2x^2-10x+12\)
Bài 3:
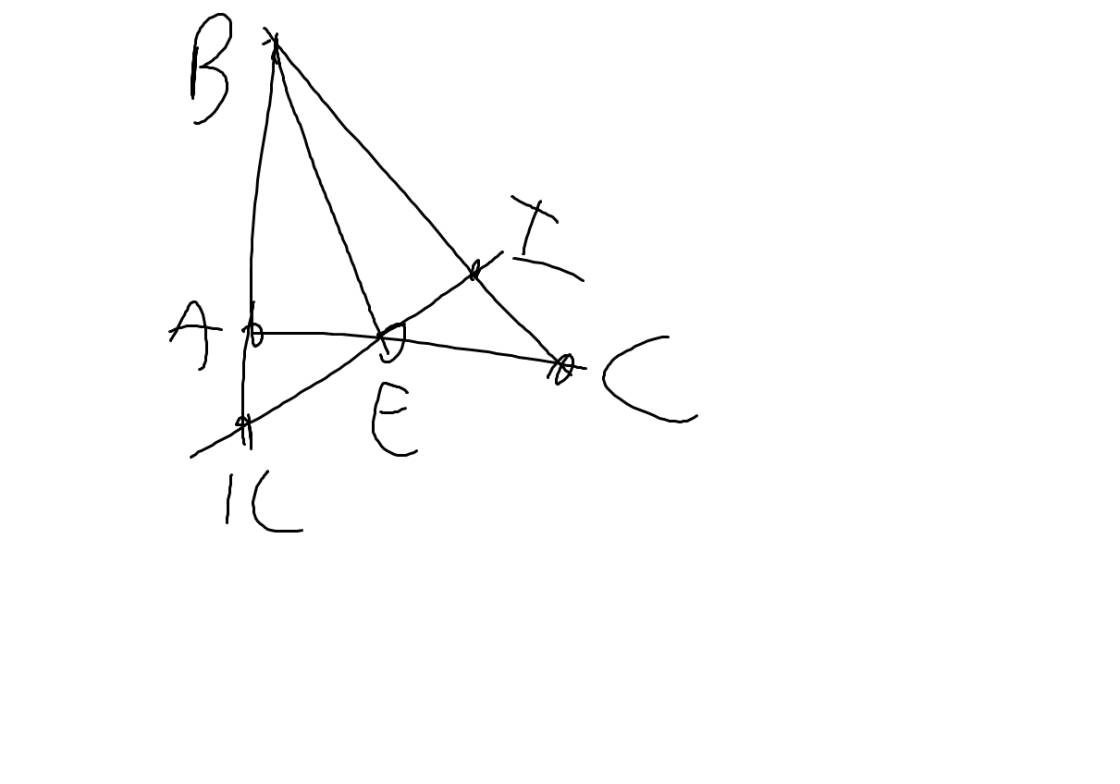
a: Xét ΔBAE và ΔBIE có
BA=BI
\(\widehat{ABE}=\widehat{IBE}\)
BE chung
Do đó: ΔBAE=ΔBIE
b: Ta có: ΔBAE=ΔBIE
=>\(\widehat{BAE}=\widehat{BIE}\)
mà \(\widehat{BAE}=90^0\)
nên \(\widehat{BIE}=90^0\)
=>EI\(\perp\)BC tại I
c: Ta có: ΔBAE=ΔBIE
=>EA=EI
Xét ΔEAK vuông tại A và ΔEIC vuông tại I có
EA=EI
\(\widehat{AEK}=\widehat{IEC}\)(hai góc đối đỉnh)
Do đó: ΔEAK=ΔEIC
=>EK=EC
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Xét ∆ABD và ∆ACD có:
AB = AC (gt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
b) Do ∠BAD = ∠CAD (cmt)
⇒ ∠EAD = ∠FAD
Xét hai tam giác vuông: ∆ADE và ∆ADF có:
AD là cạnh chung
∠EAD = ∠FAD (cmt)
⇒ ∆ADE = ∆ADF (cạnh huyền - góc nhọn)
⇒ DE = DF (hai cạnh tương ứng)
c) Do ∆ADE = ∆ADF (cmt)
⇒ AE = AF (hai cạnh tương ứng)
⇒ A nằm trên đường trung trực của EF (1)
Do DE = DF (cmt)
⇒ D nằm trên đường trung trực của EF (2)
Từ (1) và (2) ⇒ AD là đường trung trực của EF
⇒ AD ⊥ EF (*)
∆ABC có AB = AC (gt)
⇒ ∆ABC cân tại A
Mà AD là tia phân giác của ∠BAC
⇒ AD là đường trung trực của ∆ABC
⇒ AD ⊥ BC (**)
Từ (*) và (**) ⇒ EF // BC