5+4x-x+2=(5+4x).(7+5x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(x^2+5y^2+2x-4xy-10y+14\)
\(=x^2+2x\left(1-2y\right)+\left(1-2y\right)^2-\left(1-2y\right)^2+5y^2-10y+14\)
\(=\left(x-2x+1\right)^2-1-4y^2+4y+5y^2-10y+14\)
\(=\left(x-2x+1\right)^2+y^2-6y+9+4\)
\(=\left(x-2x+1\right)^2+\left(y-3\right)^2+4\ge4>0\) (đpcm)
Ta có: x2 + 5y2 + 2x - 4xy - 10y + 14
= (x2 - 4xy + 4y2) + (2x - 4y) + 1 + (y2 - 6y + 9) + 4
= (x - 2y)2 + 2(x - 2y) + 1 + (y - 3)2 + 4
= (x - 2y + 1)2 + (y - 3)2 + 4 > 0 \(\forall\)x; y
Do (x - 2y + 1)2 \(\ge\)0; (y - 3)2 \(\ge\)0 ; 4 > 0

a) \(pt\Leftrightarrow\frac{6}{x^2+2}-1+\frac{7}{x^2+3}-1+\frac{12}{x^2+8}-1-\frac{3x^2+16}{x^2+10}+2=0\)
\(\Leftrightarrow\frac{4-x^2}{x^2+2}+\frac{4-x^2}{x^2+3}+\frac{4-x^2}{x^2+8}+\frac{4-x^2}{x^2+10}=0\)
\(\Leftrightarrow\left(4-x^2\right)\left(\frac{1}{x^2+2}+\frac{1}{x^2+3}+\frac{1}{x^2+8}+\frac{1}{x^2+10}\right)=0\)
\(\Leftrightarrow4-x^2=0\)(do \(\frac{1}{x^2+2}+\frac{1}{x^2+3}+\frac{1}{x^2+8}+\frac{1}{x^2+10}>0,\forall x\))
\(\Leftrightarrow x^2=4\Leftrightarrow x=\pm2\)
\(KL...\)
2x(8x - 1)2(4x - 1) = 9
<=> 512x4 - 256x3 + 40x2 - 2x = 9
<=> 512x4 - 256x3 + 40x2 - 2x - 9 = 0
<=> (2x - 1)(4x + 1)(64x4 - 16x + 9) = 0
vì 64x4 - 16x + 9 khác 0 nên:
<=> 2x - 1 = 0 hoặc 4x + 1 = 0
<=> x = 1/2 hoặc x = -1/4

Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4
Gọi DH và BK lần lượt là khoảng cách từ D và B đến cạnh AC.
Ta có AB = AD + DB
⇒ AB = 13,5 + 4,5 = 18 (cm)
Vì DH // BK (cùng vuông góc với AC) nên áp dụng hệ quả định lí Ta-lét ta có:
Vậy tỉ số khoảng cách từ D và B đến cạnh AC là 3/4

Từ đề bài, ta suy ra:
\(x^2-x+2009\)
\(=\left(x^2-x+\frac{1}{4}\right)+2008,75\)
\(=\left(x-\frac{1}{2}\right)^2+2008,75\)
Vì \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\)nên GTNN của biểu thức là 2008,75
\(x^2-x+2019=x^2-x+\frac{1}{4}+\frac{8075}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\frac{8075}{4}\ge\frac{8075}{4}\)
Dấu "=" khi \(x=\frac{1}{2}\)

(x-3).(2x-1)=(2x-1).(2x+3)
<=> (x-3).(2x-1)-(2x-1).(2x+3)=0
<=> (x-3-2x-3)(2x-1)=0
<=> (-3x-6)(2x-1)=0
<=> -3x-6=0 hoặc 2x-1=0
<=> -3x=6 hoặc 2x=1
<=> x=-2 hoặc x=1/2
Vậy \(x\in\left\{-2;\frac{1}{2}\right\}\)
(x - 3)(2x - 1) = (2x - 1)(2x + 3)
<=> (x - 3)(2x - 1) - (2x - 1)(2x + 3) = 0
<=> (2x - 1)(x - 3 - 2x - 3) = 0
<=> (2x - 1)(-x - 6) = 0
<=> \(\orbr{\begin{cases}2x-1=0\\-x-6=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=\frac{1}{2}\\x=-6\end{cases}}\)
Vậy S = {1/2; -6}
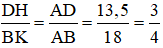
\(5+4x-x+2=\left(5x+4\right)\left(7+5x\right)\)
\(\Leftrightarrow5+4x-x+2=35+28x+25x+20x^2\)
\(\Leftrightarrow x^2+50x+28=0\)
Ta có \(\Delta=50^2-4.1.28=2388,\sqrt{\Delta}=2\sqrt{597}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-50+2\sqrt{597}}{2}=-25+\sqrt{597}\\x=\frac{-50-2\sqrt{597}}{2}=-25-\sqrt{597}\end{cases}}\)
\(5+4x-x+2=\left(5+4x\right)\left(7+5x\right)\)
\(7+3x=\left(5+4x\right)\left(7+5x\right)\)
\(7+3x=35+28x+25x+20x^2\)
\(7+3x-35-28x-25x-20x^2=0\)
\(-28-50x-20x^2=0\)
\(-28-50x-20x^2=0\)
\(x=-\frac{25+\sqrt{65}}{20};-\frac{25-\sqrt{65}}{20}\)