Xác định các giá trị của m để ptr \(x^2-x+1-m=0\) có 2 nghiệp thực x1,x2 thỏa mãn đẳng thức \(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


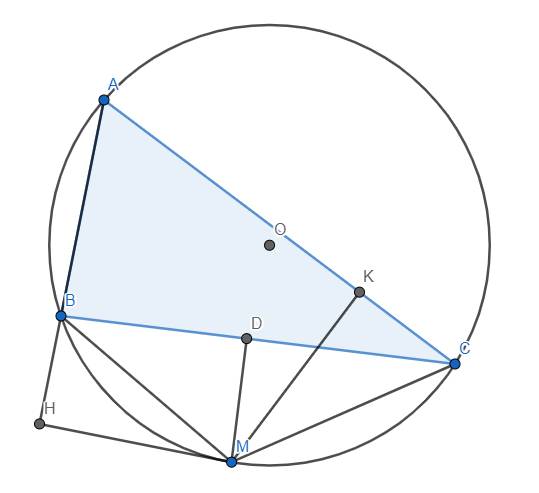
a) Theo đề bài, ta thấy \(\widehat{AHM}=\widehat{AKM}=90^o\) nên dễ dàng suy ra tứ giác AHMK nội tiếp do 2 góc đối bù nhau.
b) Do tứ giác AHMK nội tiếp nên \(\widehat{HMK}+\widehat{A}=180^o\). Tứ giác ABMC nội tiếp nên \(\widehat{BMC}+\widehat{A}=180^o\). Từ đó suy ra \(\widehat{HMK}=\widehat{BMC}\) hay \(\widehat{BMH}=\widehat{CMK}\). Lại có \(\widehat{MHB}=\widehat{MKC}=90^o\) nên \(\Delta MHB~\Delta MKC\left(g.g\right)\) \(\Rightarrow\dfrac{MH}{MK}=\dfrac{MB}{MC}\) \(\Rightarrowđpcm\)

Lời giải:
Trừ theo vế 2 pt trên ta có:
$x^3-y^3=5y-5x$
$\Leftrightarrow (x-y)(x^2+xy+y^2)+5(x-y)=0$
$\Leftrightarrow (x-y)(x^2+xy+y^2+5)=0$
Ta thấy: $x^2+xy+y^2+5=(x+\frac{y}{2})^2+\frac{3y^2}{4}+5\geq 5>0$ với mọi $x,y$
$\Rightarrow x-y=0$
$\Leftrightarrow x=y$.
Thay vào pt (1): $x^3=3x+8x=11x$
$\Leftrightarrow x(x^2-11)=0$
$\Leftrightarrow x\in\left\{0; \pm \sqrt{11}\right\}$
Vậy........

Yêu cầu đề bài là gì bạn nên ghi đầy đủ để được hỗ trợ tốt hơn.

\(\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}}=\left(\dfrac{x-1}{\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}.\dfrac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-1\)


Ta có \(\widehat{EDF}=\widehat{ECF}\) (chắn hai cung bằng nhau AI và BI của đường tròn (O))
\(\Rightarrow\) Tứ giác CDEF nội tiếp
\(\Rightarrow\widehat{DEF}+\widehat{DCF}=180^0\)
Mà \(\widehat{DCF}+\widehat{DAB}=180^0\) (tứ giác ABCD nội tiếp)
\(\Rightarrow\widehat{DEF}=\widehat{DAB}\)
\(\Rightarrow EF||AB\) (hai góc đồng vị bằng nhau)

Ta có:
\(x^2+3y^2=x^2+y^2+2y^2\ge2\sqrt{\left(x^2+y^2\right).2y^2}=2y\sqrt{2\left(x^2+y^2\right)}\)
\(\Rightarrow P=\sum\dfrac{xy}{x^2+3y^2}\le\sum\dfrac{x}{2\sqrt{2\left(x^2+y^2\right)}}=\dfrac{1}{2\sqrt{2}}\sum\sqrt{\dfrac{x^2}{x^2+y^2}}=\dfrac{1}{2\sqrt{2}}\sum\sqrt{\dfrac{a}{a+b}}\)
\(P\le\dfrac{1}{2\sqrt{2}}\sum\sqrt{a+c}.\sqrt{\dfrac{a}{\left(a+b\right)\left(a+c\right)}}\)
\(\Rightarrow P^2\le\dfrac{1}{8}\left(\sum\sqrt{a+c}.\sqrt{\dfrac{a}{\left(a+b\right)\left(a+c\right)}}\right)^2\le\dfrac{1}{8}\left(2a+2b+2c\right)\left(\dfrac{a}{\left(a+b\right)\left(a+c\right)}+\dfrac{b}{\left(a+b\right)\left(b+c\right)}+\dfrac{c}{\left(a+c\right)\left(b+c\right)}\right)\)
\(\Rightarrow P^2\le\dfrac{1}{2}.\dfrac{\left(a+b+c\right)\left(ab+bc+ca\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
Lại có \(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge\dfrac{8}{9}\left(a+b+c\right)\left(ab+bc+ca\right)\)
\(\Rightarrow P^2\le\dfrac{1}{2}.\dfrac{\left(a+b+c\right)\left(ab+bc+ca\right)}{\dfrac{8}{9}\left(a+b+c\right)\left(ab+bc+ca\right)}=\dfrac{9}{16}\)
\(\Rightarrow P\le\dfrac{3}{4}\)
Dấu "=" xảy ra khi \(a=b=c\) hay \(x=y=z\)
help me: tìm n biết 2^n + 3^n = 5^n với n E N