 mn giúp mik với ạ
mn giúp mik với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x-36\right)^{2024}>=0\forall x\)
\(\left|x-2y\right|^{2023}>=0\forall x,y\)
Do đó: \(\left(x-36\right)^{2024}+\left|x-2y\right|^{2023}>=0\forall x,y\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-36=0\\x-2y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=36\\y=18\end{matrix}\right.\)
\(D=\sqrt{x}-3y=\sqrt{36}-3\cdot18=6-54=-48\)

Gọi chiều dài các thửa ruộng A,B,C lần lượt là a(m),b(m),c(m)
(Điều kiện: a>0; b>0; c>0)
Ba thửa ruộng có diện tích bằng nhau
mà Chiều rộng các thửa ruộng A,B,C lần lượt tỉ lệ thuận với 4;5;6
nên Chiều dài các thửa ruộng A,B,C lần lượt tỉ lệ thuận với \(\dfrac{1}{4};\dfrac{1}{5};\dfrac{1}{6}\)
=>\(\dfrac{a}{\dfrac{1}{4}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{6}}\)
Chiều dài thửa ruộng A nhỏ hơn tổng chiều dài hai thửa ruộng còn lại là 42m nên b+c-a=42
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{4}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{6}}=\dfrac{b+c-a}{\dfrac{1}{5}+\dfrac{1}{6}-\dfrac{1}{4}}=\dfrac{42}{\dfrac{7}{60}}=360\)
=>\(a=360\cdot\dfrac{1}{4}=90;b=360\cdot\dfrac{1}{5}=72;c=360\cdot\dfrac{1}{6}=60\)
Vậy: chiều dài các thửa ruộng A,B,C lần lượt là 90m; 72m; 60m

f(x) + g(x) = (x⁵ - 3x² + x³ - x² - 2x + 5) + (x² - 3x + 1 + x² - x⁴ + x⁵)
= x⁵ - 3x² + x³ - x² - 2x + 5 + x² - 3x + 1 + x² - x⁴ + x⁵
= (x⁵ + x⁵) - x⁴ + x³ + (-3x² - x² + x² + x²) + (-2x - 3x) + (5 + 1)
= 2x⁵ - x⁴ + x³ - 2x² - 5x + 6
---------
f(x) - g(x) = (x⁵ - 3x² + x³ - x² - 2x + 5) - (x² - 3x + 1 + x² - x⁴ + x⁵)
= x⁵ - 3x² + x³ - x² - 2x + 5 - x² + 3x - 1 - x² + x⁴ - x⁵
= (x⁵ - x⁵) + x⁴ + x³ + (-3x² - x² - x² - x²) + (-2x + 3x) + (5 - 1)
= x⁴ + x³ - 6x² + x + 4

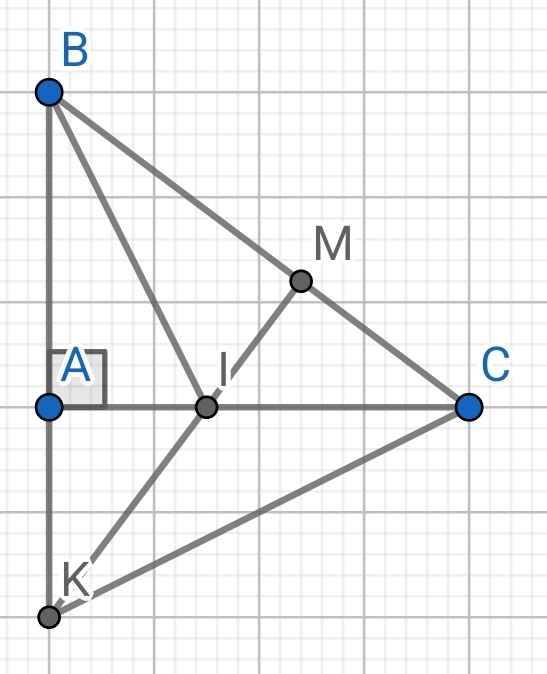
a) ∆ABC vuông tại A (gt)
⇒ ∠ABC + ∠ACB = 90⁰
⇒ ∠ACB = 90⁰ - ∠ABC
= 90⁰ - 55⁰ = 35⁰
b) Xét hai tam giác vuông: ∆ABI và ∆MBI có:
AB = BM (gt)
BI là cạnh chung
⇒ ∆ABI = ∆MBI (cạnh huyền - cạnh góc vuông)
c) Do ∆ABI và ∆MBI (cmt)
⇒ AI = MI (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆AIK và ∆MIC có:
AI = MI (cmt)
∠AIK = ∠MIC (đối đỉnh)
⇒ ∆AIK = ∆MIC (cạnh góc vuông - góc nhọn kề)
⇒ IK = IC (hai cạnh tương ứng)
d) ∆BIC có:
∠BIC = ∠BAI + ∠ABI (góc ngoài của ∆ABI)
= 90⁰ + ∠ABI > 90⁰
⇒ ∠BIC là góc tù
⇒ ∠BIC là góc lớn nhất
⇒ CB là cạnh lớn nhất (cạnh đối diện với góc lớn nhất)
⇒ IB < CB (1)
∆KIC có:
∠KIC = ∠KAI + ∠AKI (góc ngoài của ∆KIA)
= 90⁰ + ∠AKI > 90⁰
⇒ ∠KIC là góc tù
⇒ ∠KIC là góc lớn nhất
⇒ CK là cạnh lớn nhất (cạnh đối diện với góc lớn nhất)
⇒ IK < CK (2)
Từ (1) và (2) ⇒ IB + IK < CB + CK

Lời giải:
$a+9\vdots 6; b+2011\vdots 6$
$\Rightarrow a+9+b+2011\vdots 6$
$\Rightarrow a+b+2020\vdots 6$
$\Rightarrow a+b+4+336.6\vdots 6$
$\Rightarrow a+b+4\vdots 6$
$\Rightarrow a+b+4=6m$ với $m$ nguyên dương
$\Rightarrow a+b=6m-4$
Mặt khác:
$4^a\equiv 1^a\equiv 1\pmod 3$. Mà $4^a\vdots 2$ với mọi số nguyên dương $a$ nên $4^a$ có dạng $6k+4$ với $k$ nguyên dương
Do đó:
$4^a+a+b=6k+4+6m-4=6(k+m)\vdots 6$ (đpcm)

Lời giải:
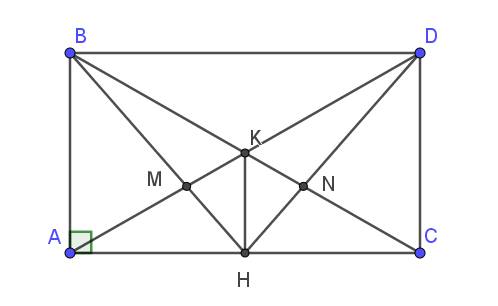
a/ Xét tam giác $BKA$ và $CKD$ có:
$BK=CK$ (do $K$ là trung điểm $BC$)
$KA=KD$
$\widehat{BKA}=\widehat{CKD}$ (đối đỉnh)
$\Rightarrow \triangle BKA=\triangle CKD$ (c.g.c)
$\Rightarrow \widehat{BAK}=\widehat{CDK}$. Mà hai góc này ở vị trí so le trong nên $CD\parallel AB$
b.
Từ $CD\parallel AB, AB\perp AC$ nên $CD\perp AC$
$\Rightarrow \widehat{DCH}=90^0$
Từ $\triangle BKA=\triangle CKD\Rightarrow AB=CD$
Xét tam giác $BAH$ và $DCH$ có:
$AH=CH$
$AB=CD$
$\widehat{BAH}=\widehat{DCH}=90^0$
$\Rightarrow \triangle BAH=\triangle DCH$ (c.g.c)
$\Rightarrow \widehat{H_1}=\widehat{H_2}$
Xét tam giác $BAC$ và $DCA$ có:
$AB=CD$
$\widehat{BAC}=\widehat{DCA}=90^0$
$AC$ chung
$\Rightarrow \triangle BAC=\triangle DCA$ (c.g.c)
$\Rightarrow \widehat{A_1}=\widehat{C_1}$
Xét tam giác $AMH$ và $CNH$ có:
$\widehat{A_1}=\widehat{C_1}$
$\widehat{H_1}=\widehat{H_2}$
$AH=CH$
$\Rightarrow \triangle AMH=\triangle CNH$ (g.c.g)
$\Rightarrow MH=NH$
$\Rightarrow MNH$ cân tại $H$
c.
Từ $\triangle BAC=\triangle DCA\Rightarrow BC=DA\Rightarrow BC:2=DA:2\Rightarrow CK=AK$
Xét tam giác $KHA$ và $KHC$ có:
$KH$ chung
$AK=CK$
$AH=CH$
$\Rightarrow \triangle KHA=\triangle KHC$ (c.c.c)
$\Rightarrow \widehat{AKH}=\widehat{CKH}$
$\Rightarrow KH$ là phân giác $\widehat{AKC}$



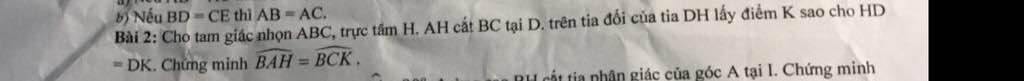
Đặt \(P\left(x\right)=ax+b\left(a\ne0\right)\)
P(1)=9 nên \(a\cdot1+b=9\)
=>a+b=9
P(-1)=-1
=>\(a\cdot\left(-1\right)+b=-1\)
=>-a+b=-1
=>a-b=1
mà a+b=9
nên \(a=\dfrac{1+9}{2}=5;b=9-5=4\)
=>P(x)=5x+4
\(P\left(0\right)=5\cdot0+4=4\)