Cho số có hai chữ số, tổng hai chữ số đó là 10. Nếu đổi chỗ hai số đó cho nhau ta được một số lớn hơn số đã cho là 18 đơn vị.Tìm số đã cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số phải tìm là ab(0<a,b≤9)
ta có tổng hai chữ số là 12
=> a+b=12<=> a=12-b
lại có Nếu đổi chỗ hai chữ số thì ta được số mới lớn hơn số cũ là 36
ab - ba = 36<=> 9a-9b =36<=> a-b = 4<=> 12 - 2b=4<=> b=4=> a=8
=> số cần tìm là 84
Tham Khảo nhé

Giả sử \(x=2\Rightarrow2^3=3^y+7\)
\(\Leftrightarrow8=3^y+7\)
\(\Leftrightarrow3^y=1\Rightarrow y=0\)
Vậy x=2; y=0 là nghiệm của phương trình

Bài làm
x4 + 2x + 2
= x4 - 2x3 + 2x + 4 - 2 + 2x3
= x3( x + 2 ) + 2( x + 2 ) - ( 2x3 + 2 )
= ( 2x3 + 2 )( x + 2 ) - ( 2x3 + 2 )
= ( 2x3 + 2 )( x + 2 - 1 )
= ( 2x3 + 2 )( x + 1 )

a) x(x-y) + y(x+y) = x^2 - xy + yx + y^2 = x^2 + y^2 = (-6)^2 + 8^2 = 100
b) x(x^2 - y ) - x^2( x + y ) + y(x^2 - x )
= x^3 - xy - x^3 -x^2y+yx^2 - xy
= ( x^3 - x^3 ) + ( x^2 y - x^2 y ) + ( -xy - xy )
= -2xy
Bạn kiểm tra lại đề nhé!


Gọi số tự nhiên có 2 chữ số đã cho là ab \(\left(0\le a;b\le9,a\ne0,a,b\in N\right)\)
Theo giả thiết ta có hệ phương trình sau:
\(\hept{\begin{cases}a+b=14\\\overline{ba}-\overline{ab}=18\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a+b=14\\\left(10b+a\right)-\left(10a+b\right)=18\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a+b=14\\9b-9a=18\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a+b=14\\b-a=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=6\\b=8\end{cases}}\)
Vậy số đã cho là 68

+) Câu d sửa đề thành BF . BA + CE . CA = BC2
a, Xét △AFH vuông tại F và △ADB vuông tại D
Có: FAH là góc chung
=> △AFH ᔕ △ADB (g.g)
b, Vì △AFH ᔕ △ADB (cmt) \(\Rightarrow\frac{AF}{AD}=\frac{AH}{AB}\)\(\Rightarrow\frac{AB}{AD}=\frac{AH}{AF}\)
Xét △ABH và △ADF
Có: \(\frac{AB}{AD}=\frac{AH}{AF}\)(cmt)
BAH là góc chung
=> △ABH ᔕ △ADF (c.g.c)
c, Xét △HFB vuông tại F và △HEC vuông tại E
Có: FHB = EHC (2 góc đối đỉnh)
=> △HFB ᔕ △HEC (g.g)
\(\Rightarrow\frac{HF}{HE}=\frac{HB}{HC}\)
=> HF . HC = HE . HB
d, Sửa đề thành BF . BA + CE . CA = BC2
Xét △HEC vuông tại E và △AFC vuông tại F
Có: HCE là góc chung
=> △HEC ᔕ △AFC (g.g)
\(\Rightarrow\frac{EC}{FC}=\frac{HC}{AC}\)
=> FC . HC = EC . AC (1)
Xét △HFB vuông tại F và △AEB vuông tại E
Có: FBH là góc chung
=> △HFB ᔕ △AEB (g.g)
\(\Rightarrow\frac{FB}{EB}=\frac{HB}{AB}\)
=> FB . AB = EB . HB (2)
Xét △BFC vuông tại F và △HDC vuông tại D
Có: HCD là góc chung
=> △BFC ᔕ △HDC (g.g)
\(\Rightarrow\frac{FC}{DC}=\frac{BC}{HC}\)
=> FC . HC = BC . DC (3)
Xét △BEC vuông tại E và △BDH vuông tại D
Có: HBD là góc chung
=> △BEC ᔕ △BDH (g.g)
\(\Rightarrow\frac{BC}{BH}=\frac{BE}{DB}\)
=> BC . DB = BE . BH (4)
Từ (1) và (3) => EC . AC = BC . DC
Từ (2) và (4) => FB . AB = BC . DB
Ta có: BF . BA + CE . CA = BC . BD + BC . DC = BC . (BD + DC) = BC . BC = BC2

*Phương trình 1:
A. \(3x+5=2\left(x-1\right)+4\)
Vậy phương trình A là phương trình một ẩn số vì có một ẩn x
*Phương trình 2:
\(y^3-y=2y^2+5\)
Vậy phương trình B là phương trình một ẩn số vì có một ẩn x
*Phương trình 3:
\(4x^2=5y\)
Vậy phương trình C là phương trình có hai ẩn nên không phải là phương trình có một ẩn số
*Phương trình D:
\(\left(5x-1\right)^3=x^3+2x+4\)
Vậy phương trình D là phương tình có một ẩn số là x
Đáp án đúng: C
Họcc tốtt.
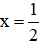 và y = –100;
và y = –100;
Gọi số dã cho là xy \(\left(10\le xy\le99;x,y>0\right)\)
Tổng hai chữ số là 10 \(\Rightarrow x+y=10\)
Nếu đổi chỗ cho nhau ta được một số lớn hơn số đã cho là 18 dơn vị \(yx-xy=18\)
\(\Leftrightarrow10y+x-10x-y=18\)
\(\Leftrightarrow-9x+9y=18\)
\(\Leftrightarrow x-y=-2\)
Ta có hệ phương trình \(\hept{\begin{cases}x+y=10\\x-y=-2\end{cases}\Leftrightarrow\hept{\begin{cases}2x=8\\x+y=10\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=4\\y=6\end{cases}}\)
Vậy số đã cho là 46