Để chứng minh rằng đa thức M=(2x+1)(5x-3)-(5x+2)(2x-7) không phụ thuộc vào biến x, ta sẽ chứng minh rằng M không chứa biến x. Đầu tiên, ta sẽ phân tích đa thức M:

M = (2x+1)(5x-3) - (5x+2)(2x-7) = 10x^2 - 6x + 5x - 3 - 10x^2 + 14x - 5x - 14 = 10x^2 - x - 3 - 10x^2 - 5x - 14 = -6x - 17

Ta thấy rằng đa thức M không chứa biến x, nên ta kết luận rằng đa thức M=(2x+1)(5x-3)-(5x+2)(2x-7) không phụ thuộc vào biến x.

đc ko bn

Sửa đề: tia phân giác của góc A

ΔABC cân tại A

mà AK là đường phân giác

nên AK là đường trung tuyến

Xét ΔABC có

AK,BD là các đường trung tuyến

AK cắt BD tại K

Do đó: K là trọng tâm của ΔABC

Xét ΔABC có

K là trọng tâm

I là trung điểm của AB

Do đó: C,K,I thẳng hàng

a, Do tam giác ABD và ACE là tam giác đều nên ta có:

∠ABD = ∠ACE = 60°
∠BAD = ∠CAE = 60°
Do tam giác ABC vuông tại A nên ∠BAC = 90°. Từ đó suy ra ∠BAE = ∠CAD = 30°.

Vậy tam giác ABE và tam giác ADC đều là tam giác vuông cân tại A, do đó tam giác ABE = tam giác ADC.

b, Gọi H là giao điểm của AD và BE. Do tam giác ABE và tam giác ADC bằng nhau nên AH = AD.

Từ đó suy ra ∠BHE = ∠DHE. Do EH là đường cao của cả hai tam giác BHD và DHE nên tam giác BHE = tam giác DHE.

Vậy ta có DE = BE.

Các điều kiện về $x,y$ là gì bạn nên ghi chú rõ ra để mọi người hỗ trợ nhé.

Lời giải:

Nếu $x\geq 2$ thì:

$P=x-1+2024(x-2)+2025=2025x-2024\geq 2025.2-2024=2026$

Nếu $1\leq x< 2$ thì:

$P=x-1+2024(2-x)+2025=6072-2023x> 6072-2023.2=2026$

Nếu $x< 1$ thì:

$P=1-x+2024(2-x)+2025=6073-2025x> 6073-2025.1=4048$

Từ 3 TH trên suy ra $P_{\min}=2026$. Giá trị này đạt tại $x\geq 2$

bạn nhớ vote cho mình nhaa

a) Vì tam giác ABC cân tại A nên ta có:

Góc BAC = Góc BCA = 47^o
Góc ABC = 180o - 2 x 47^o = 86^o
b) Ta có:

AB = AC (do tam giác ABC cân tại A)
BM = MC (do M là trung điểm của BC)
∠ABM = ∠ACM = 90^o - 47^o = 43^o (do ∠BAC = 47^o và ∠BAM, ∠CAM là góc vuông) 
Vậy, 𝛥𝐴𝐵𝑀 = 𝛥𝐴𝐶𝑀 (theo định lý tam giác cân)
c) Ta có:

AM + BM = AB + BM (do AB = AM)
AB + BM > AC (do tổng độ dài hai cạnh của một tam giác luôn lớn hơn cạnh còn lại) 
Vậy, AM + BM > AC

Bài 3

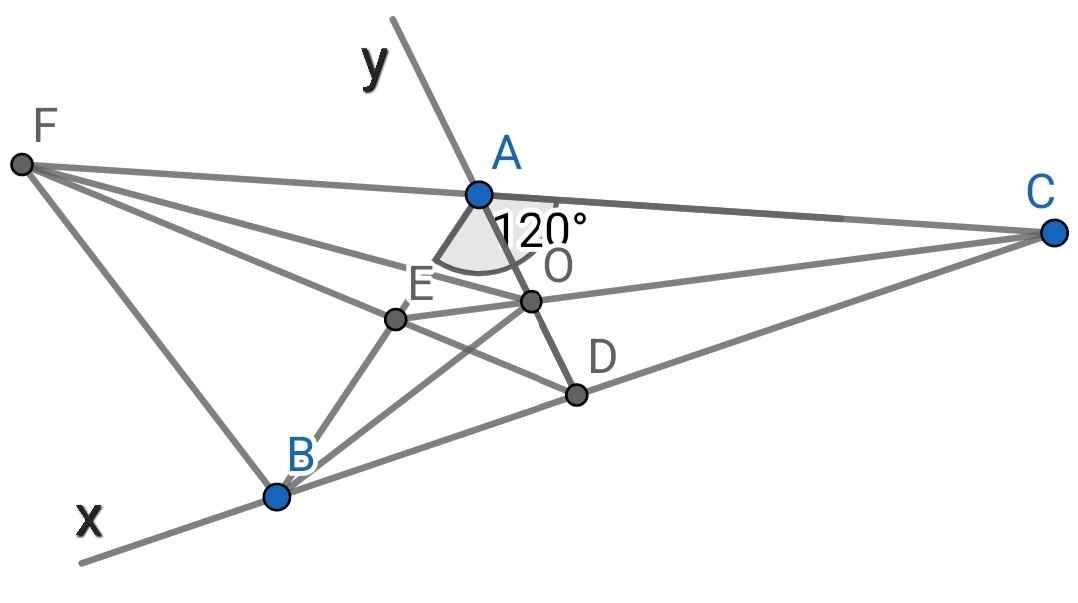
a) ∆ABC có:

AD và CE là hai đường phân giác (gt)

O là giao điểm của AD và CE (gt)

⇒ BO là đường phân giác thứ ba của ∆ABC

⇒ BO là tia phân giác của ∠ABC

b) Vẽ tia Ay là tia đối của tia AD

Ta có:

∠BAF + ∠BAC = 180⁰ (kề bù)

⇒ ∠BAF = 180⁰ - ∠BAC

= 180⁰ - 120⁰

= 60⁰

Do AD là tia phân giác của ∠BAC (gt)

⇒ ∠BAD = ∠CAD = ∠BAC : 2

= 120⁰ : 2

= 60⁰

⇒ ∠FAy = ∠CAD = 60⁰ (đối đỉnh)

⇒ AF là tia phân giác của ∠BAy

⇒ AF là tia phân giác tại góc ngoài đỉnh A của ∆ABD

Lại có BF là tia phân giác tại góc ngoài đỉnh B của ∆ABD (gt)

⇒ DF là tia phân giác của ∠ADB

⇒ ∠BDF = ∠FDA

c) Ta có:

∠BAF = ∠BAD = 60⁰

⇒ AB là tia phân giác của ∠FAD

⇒ AB là tia phân giác của góc ngoài tại đỉnh A của ∆ACD

∆ACD có:

AB là tia phân giác tại góc ngoài đỉnh A của ∆ACD (cmt)

CE là tia phân giác của góc trong tại đỉnh C của ∆ACD (gt)

Mà E là giao điểm của AB và CE (gt)

⇒ DE là tia phân giác của ∠ADB

Lại có DF là tia phân giác của ∠ADB (cmt)

⇒ D, E, F thẳng hàng

Bài 4

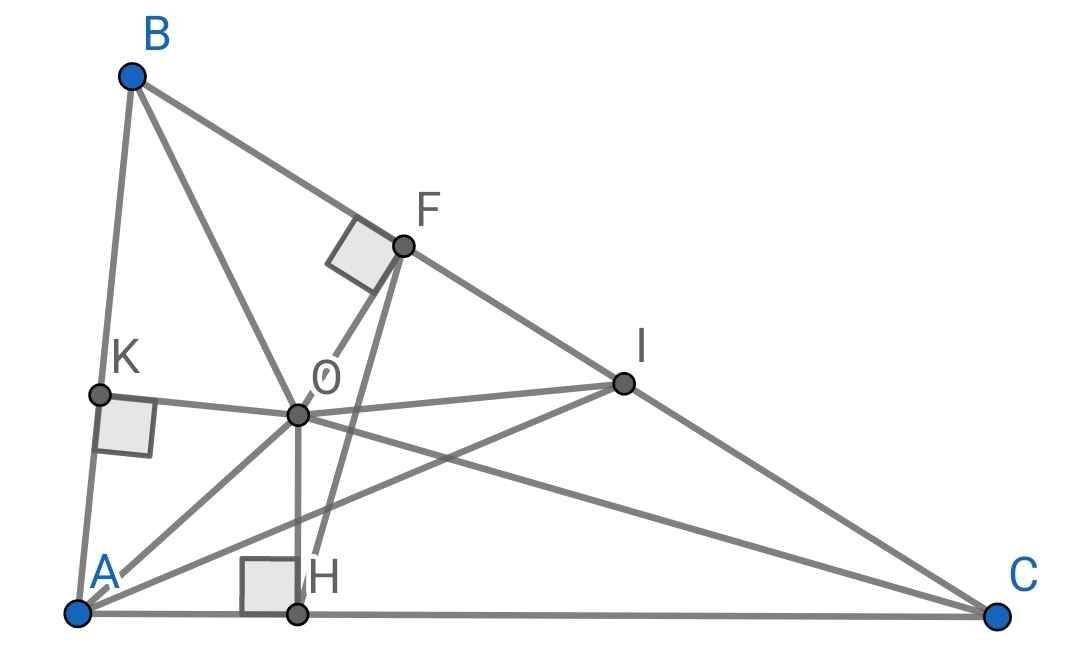
a) Do CO là tia phân giác của ∠ACB (gt)

⇒ ∠ACO = ∠BCO

⇒ ∠HCO = ∠FCO

Xét hai tam giác vuông: ∆CHO và ∆CFO có:

CO là cạnh chung

∠HCO = ∠FCO (cmt)

⇒ ∆CHO = ∆CFO (cạnh huyền - góc nhọn)

⇒ CH = CF (hai cạnh tương ứng)

⇒ C nằm trên đường trung trực của FH (1)

Do O nằm trên hai đường phân giác của ∆ABC (gt)

⇒ OH = OF

⇒ O nằm trên đường trung trực của FH (2)

Từ (1) và (2) ⇒ OC là đường trung trực của FH

⇒ OC ⊥ FH

b) Nối BO

Do AO và CO là hai đường phân giác của ∆ABC cắt nhau tại O

⇒ BO là tia phân giác của ∠ABC

Vẽ OK ⊥ AB

Do O là giao điểm của hai tia phân giác của ABC (gt)

⇒ OH = OK = OF

Xét hai tam giác vuông: ∆OHA và ∆OFI có:

OH = OF (cmt)

AH = FI (gt)

⇒ ∆OHA = ∆OFI (hai cạnh góc vuông)

⇒ OA = OI (hai cạnh tương ứng)

⇒ ∆OAI cân tại O

Xét hai tam giác vuông: ∆BOK và ∆BOF có:

BO là cạnh chung

OK = OF (cmt)

⇒ ∆BOK = ∆BOF (cạnh huyền - cạnh góc vuông)

⇒ BK = BF (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆OKA và ∆OFI có:

OK = OF (cmt)

OA = OI (cmt)

⇒ ∆OKA = ∆OFI (cạnh huyền - cạnh góc vuông)

⇒ AK = FI (hai cạnh tương ứng)

Ta có:

BA = BK + AK

BI = BF + FI

Mà BK = BF (cmt)

AK = FI (cmt)

⇒ BA = BI

⇒ ∆BAI cân tại B

Xét ΔAMB và ΔIMC có:

MA = MI (do cách vẽ)
∠AMB = ∠IMC (do hai góc đối đỉnh)
MB = MC (do M là trung điểm của BC)
Suy ra ΔAMB = ΔIMC (c.g.c) => AB = IC (hai cạnh tương ứng), mà ∠A1 = ∠A2 (Vì AM là tia phân giác của ∠BAC) => ∠A2 = ∠I1 => ΔACI cân tại C => AC = IC và mà AB = IC => AB = AC.
Vậy ΔABC cân tại A.

Bạn ghi câu hỏi đầy đủ ra được không?

a: Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED

b: Ta có: ΔBAD=ΔBED

=>DA=DE

Ta có: ΔBAD=ΔBED

=>\(\widehat{BAD}=\widehat{BED}=90^0\)

=>DE\(\perp\)BC tại E

Xét ΔDAK vuông tại A và ΔDEC vuông tại E có

DA=DE

\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó; ΔDAK=ΔDEC

=>AK=EC

c: Ta có; ΔDAK=ΔDEC

=>DK=DC 

=>D nằm trên đường trung trực của KC(1)

Ta có: IK=IC

=>I nằm trên đường trung trực của KC(2)

Ta có: BA+AK=BK

BE+EC=BC
mà BA=BE và AK=EC

nên BK=BC

=>B nằm trên đường trung trực của KC(3)

Từ (1),(2),(3) suy ra B,D,I thẳng hàng

A) Chứng minh Tam giác BAD = Tam giác BED

Xét hai tam giác BAD và BED, ta có:

BA = BE (theo giả thiết)
∠BAD = ∠BED (do DE là tia phân giác của ∠B)
Do đó, tam giác BAD = tam giác BED (theo trường hợp cạnh - góc - cạnh).

B) Chứng minh AK = EC

Do tam giác BAD = tam giác BED, ta có AD = ED.

Gọi K là giao điểm của BA và DE, ta có:

AK + KD = AD
EK + KD = ED
Do AD = ED, suy ra AK + KD = EK + KD. Do đó, AK = EK.

C) Chứng minh ba điểm B, D, I thẳng hàng

Gọi I là trung điểm của CK. Do AK = EK và AI = IC (do I là trung điểm), ta có tam giác AKE = tam giác ICE (theo trường hợp cạnh - cạnh - cạnh).

Do đó, ∠AKE = ∠ICE. Khi đó, ta có ∠BKI = ∠BID. Do đó, B, D, I thẳng hàng.