Học sinh lớp 6A được giao một số lượng cây trồng trong 3 ngày .Ngày thứ nhất trồng được 3/8 số trang .Ngày thứ hai trồng được 4/7 số cây còn lại .Ngày thứ ba trồng được 15 cây .Tính số cây học sinh lớp 6A trồng được trong 3 ngày
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) vì M nằm giữa đoạn thẳng AB nên ta có :
AM + MB = AB
AM + MB = 12 cm
Mà MA = MB = 12 : 2 = 6 cm
Vậy MB dài 6cm
b) Câu b bị thiếu đề nên mik ko giải dc =(

Lời giải:
\(1-A=\frac{10^{2023}-10^{2022}}{10^{2023}+2024}=\frac{9.10^{2022}}{10^{2023}+2024}=\frac{9}{10+\frac{2024}{10^{2022}}}< \frac{9}{10}=1-\frac{1}{10}=1-\frac{10^{2023}}{10^{2024}}=1-B\)
$\Rightarrow A>B$

Lời giải:
Vì số tự nhiên đó chia 17 dư 7 nên đặt nó là $A=17k+7$ với $k$ là số tự nhiên.
$A=17k+7$ chia 7 dư 4
$\Rightarrow 17k+7-4\vdots 7$
$\Rightarrow 17k+3\vdots 7$
$\Rightarrow 17k+3+14\vdots 7$
$\Rightarrow 17(k+1)\vdots 7\Rightarrow k+1\vdots 7$
$\Rightarrow k=7m-1$ với $m$ tự nhiên.
Khi đó: $A=17k+7=17(7m-1)+7=119m-10=119(m-1)+109$
Vậy số đó chia 119 dư 109.

a: Dãy dữ liệu này là số liệu
b: Chỗ không hợp lí là số 94, vì khó có chuyện mà một lớp có 94 bạn
biểu thức a=3/2n+1. tìm só nguyên n để a là số nguyên mọi người ơi cứu em,mai thi rồi.Tks nhiều ạ!!!

ĐKXĐ: \(n\ne-\dfrac{1}{2}\)
Để A là số nguyên thì \(3⋮2n+1\)
=>\(2n+1\in\left\{1;-1;3;-3\right\}\)
=>\(2n\in\left\{0;-2;2;-4\right\}\)
=>\(n\in\left\{0;-1;1;-2\right\}\)

\(S=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dots+\dfrac{1}{2024^2}\)
+, Ta thấy:
\(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
\(\dfrac{1}{4^2}< \dfrac{1}{3.4}\)
\(...\)
\(\dfrac{1}{2024^2}< \dfrac{1}{2023.2024}\)
Suy ra: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2024^2}\)
\(< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dots+\dfrac{1}{2023.2024}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dots+\dfrac{1}{2023}-\dfrac{1}{2024}\)
\(=1-\dfrac{1}{2024}< 1\)
\(\Rightarrow S< 1\) (1)
+, Lại có: \(\dfrac{1}{2^2}>0\)
\(\dfrac{1}{3^2}>0\)
\(\dfrac{1}{4^2}>0\)
\(...\)
\(\dfrac{1}{2024^2}>0\)
Suy ra: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2024^2}>0\)
\(\Rightarrow S>0\) (2)
Từ (1) và (2) \(\Rightarrow0< S< 1\)
\(\Rightarrow\) S không phải là số tự nhiên
$Toru$

a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(50^0< 120^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
b: Ta có: tia Ot nằm giữa hai tia Ox và Oy
=>\(\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\)
=>\(\widehat{tOy}+50^0=120^0\)
=>\(\widehat{tOy}=70^0\)
c: Ta có: \(\widehat{xOt}+\widehat{tOz}=\widehat{xOz}\)
=>\(\widehat{tOz}+50^0=180^0\)
=>\(\widehat{tOz}=130^0\)

m3 = 75.n (m; n ϵ N*)
m3 - 75n = 0
Ta có: 75 = 1 x 75 = 3 x 25 = 15 x 5
Lập phương nhỏ nhất từ các tích trên:
\(1\times75\rightarrow75^3\)
\(3\times25\rightarrow75^3\)
\(15\times5\rightarrow15\times5\times3\times15\rightarrow15^3\)
Do 153 là giá trị nhỏ nhất ⇒ m = 15
⇒ n = 153 : 75 = 45
Vậy m = 15 và n = 45.

\(2\left(x+\dfrac{-5}{2}\right)^2+\dfrac{-5}{12}=\dfrac{1}{12}\)
=>\(2\left(x-\dfrac{5}{2}\right)^2=\dfrac{1}{12}+\dfrac{5}{12}=\dfrac{6}{12}=\dfrac{1}{2}\)
=>\(\left(x-\dfrac{5}{2}\right)^2=\dfrac{1}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{5}{2}=\dfrac{1}{2}\\x-\dfrac{5}{2}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
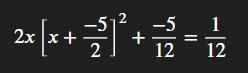
Sau ngày thứ nhất thì số cây còn lại chiếm:
\(1-\dfrac{3}{8}=\dfrac{5}{8}\)(tổng số cây)
15 cây cuối cùng chiếm: \(\dfrac{5}{8}\cdot\left(1-\dfrac{4}{7}\right)=\dfrac{5}{8}\cdot\dfrac{3}{7}=\dfrac{15}{56}\)(tổng số cây)
Tổng số cây là \(15:\dfrac{15}{56}=56\left(cây\right)\)