Gieo 1 hạt xúc xắc 6 mặt 1 lần. Tính xác suất để khi "gieo được số
chấm lớn hơn 5"
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


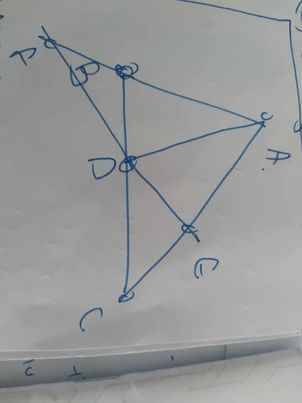
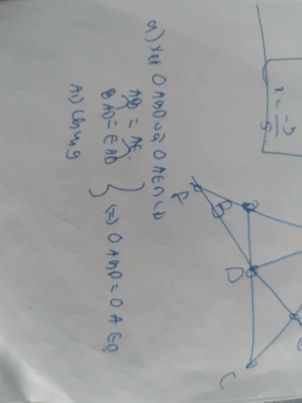
a) Vì ΔABC cân tại A nên ∠BAC = ∠ABC = 80o. Do đó, ∠BCA = 180o - 2 x 80o = 20o. Vì tam giác ABC cân tại A nên AB = AC.
b) ΔABM và ΔACM có:
∠BAM = ∠CAM (do ∠BAC = ∠ABC)
∠ABM = ∠ACM = 90o (do AM là trung tuyến)
AB = AC (do ΔABC cân tại A) Vậy ΔABM = ΔACM theo nguyên lý góc - cạnh - góc.
c) Để chứng minh AG = 2GM, ta dùng định lý về tỉ số đoạn trên trung tuyến trong tam giác:
Trong ΔABM và ΔACM, ta có ∠BAM = ∠CAM và ∠ABM = ∠ACM. Do đó, ∠BMA = ∠CMA.
Vì BN là trung tuyến của ΔABC, nên BN // AC và BN = \(\dfrac{1}{2}\) AC.
Do đó, ∠BNG = ∠CMA.
Vì ∠BMA = ∠CMA và ∠BNG = ∠CMA, nên ∠BNG = ∠BMA. Do đó, ΔBNG = ΔBMA.
Từ đó, ta có \(\dfrac{BG}{BM}\) = \(\dfrac{NG}{NA}\) = \(\dfrac{1}{2}\), suy ra AG = BG - BA = BG - NG = 2GM.
a, Tam giác ABC cân tại A
=> góc ABC = góc ACB
Xét tam giác ABC cân tại A: góc BAC + góc ABC + góc ACB = 180° (định lí tổng 3 góc trong 1 tam giác)
mà ABC = ACB (cmt)
=> BAC + 2ABC = 180°
⇔ 80° + 2ABC = 180°
2ABC = 100°
ABC = ACB = 50°
So sánh các cạnh của tam giác ABC: AB = AC (tam giác ABC là tam giác cân)
b, Xét tam giác ABM và tam giác ACM:
+ AB = AC (cmt)
+ góc ABC = góc ACB (cmt)
+ BM = CM (AM là đường trung tuyến của tam giác ABC)
=> Tam giác ABM = tam giác ACM (c.g.c) (đpcm)
c, Xét tam giác ABC có hai đường trung tuyến BN và AM cắt nhau tại G (gt)
=> G là trọng tâm của tam giác ABC
=> AG/AM = 2/3; GM/AM = 1/3
=> AG/GM = 2
⇔ AG = 2GM (đpcm)

THAM KHẢO:
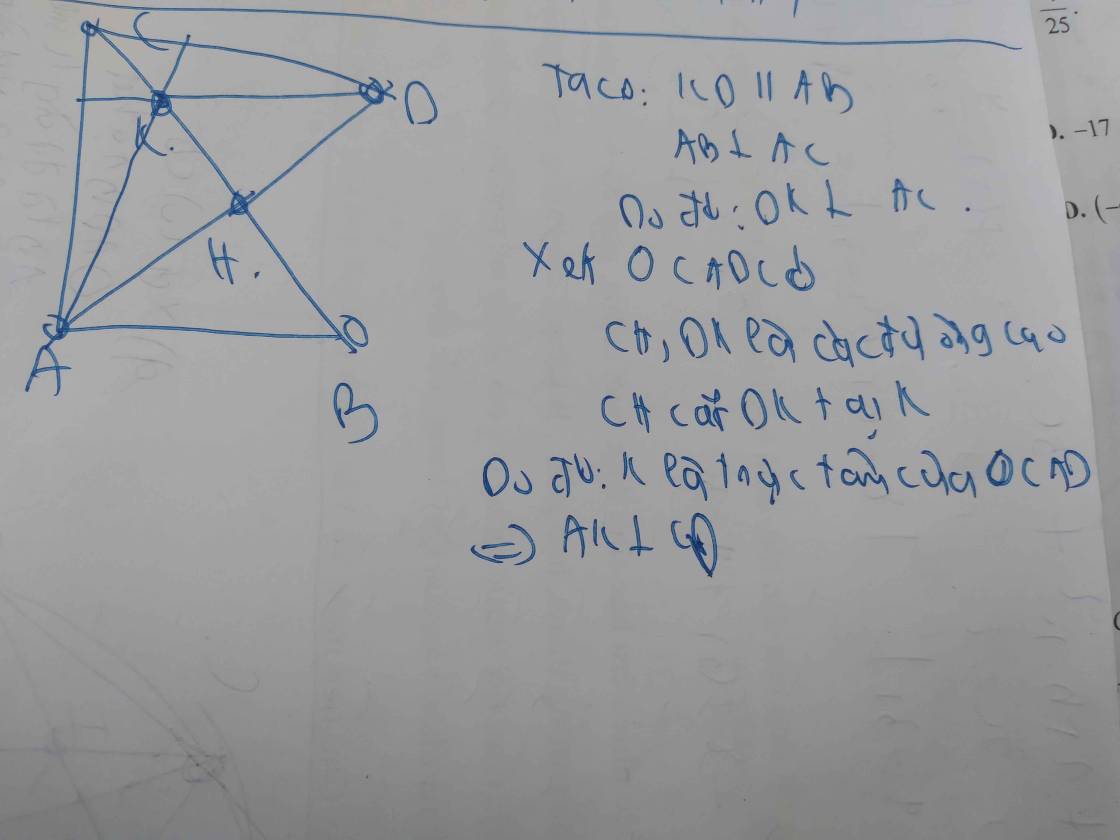
Ta có: AH là đường cao
=> CH vuông góc với AH
hay CH vuông góc với AD (1)
Ta có: DK // AB (gt)
=> DK vuông góc với AC (2) (AB vuông góc với AC, tam giác ABC vuông tại A)
Từ (1) và (2)
=> DK và CH là hai đường cao của tam giác ADC
Mà DK và CH cắt nhau tại K (K nằm trên HC)
=> K là trực tâm của tam giác ADC
Trong tam giác ADC có: AK cắt HC tại K
=> AK vuông góc CD (K là trực tâm của tam giác ADC) (đpcm)

=>BD=DE
=>D nằm trên đường trung trực của BE(1)
Ta có: AB=AE
=>A nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra AD là đường trung trực của BE
=>AD\(\perp\)BE
b: Ta có: ΔABD=ΔAED
=>\(\widehat{ABD}=\widehat{AED}\)
mà \(\widehat{ABD}+\widehat{DBF}=180^0\)(hai góc kề bù)
và \(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
nên \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDBF=ΔDEC
d: Xét ΔABC có AD là phân giác
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
mà AB<AC
nên BD<CD
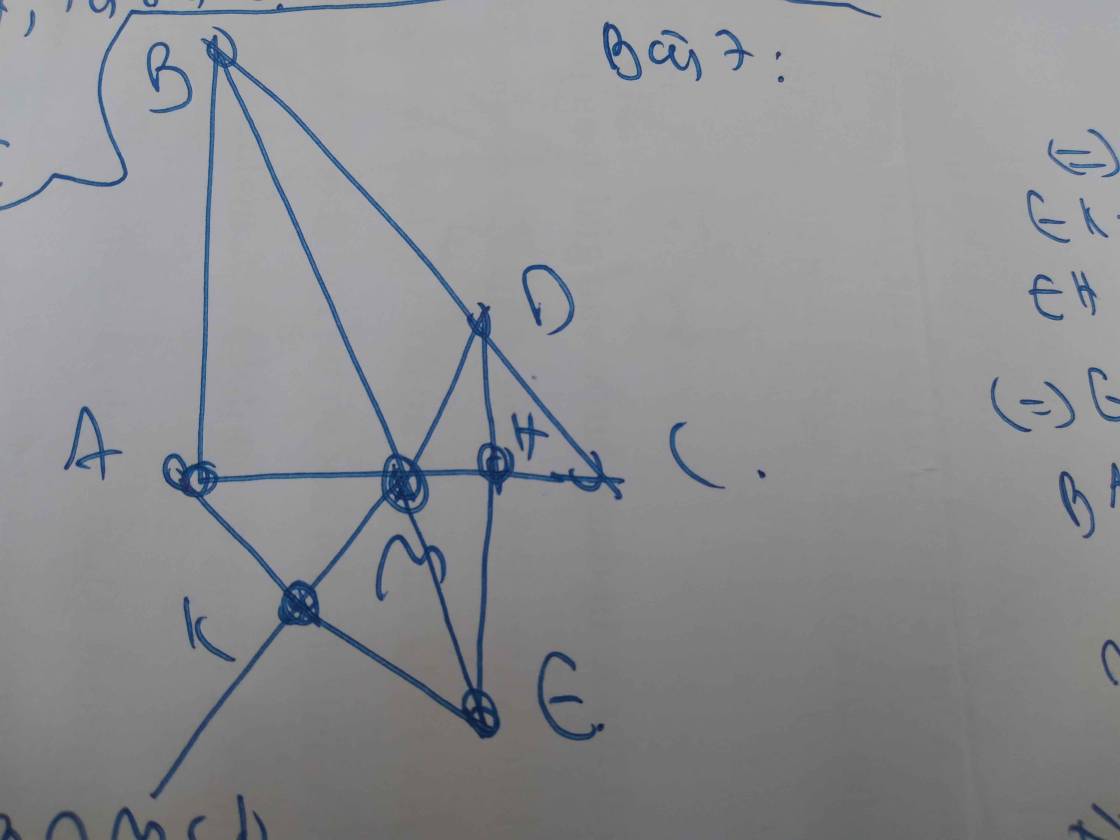
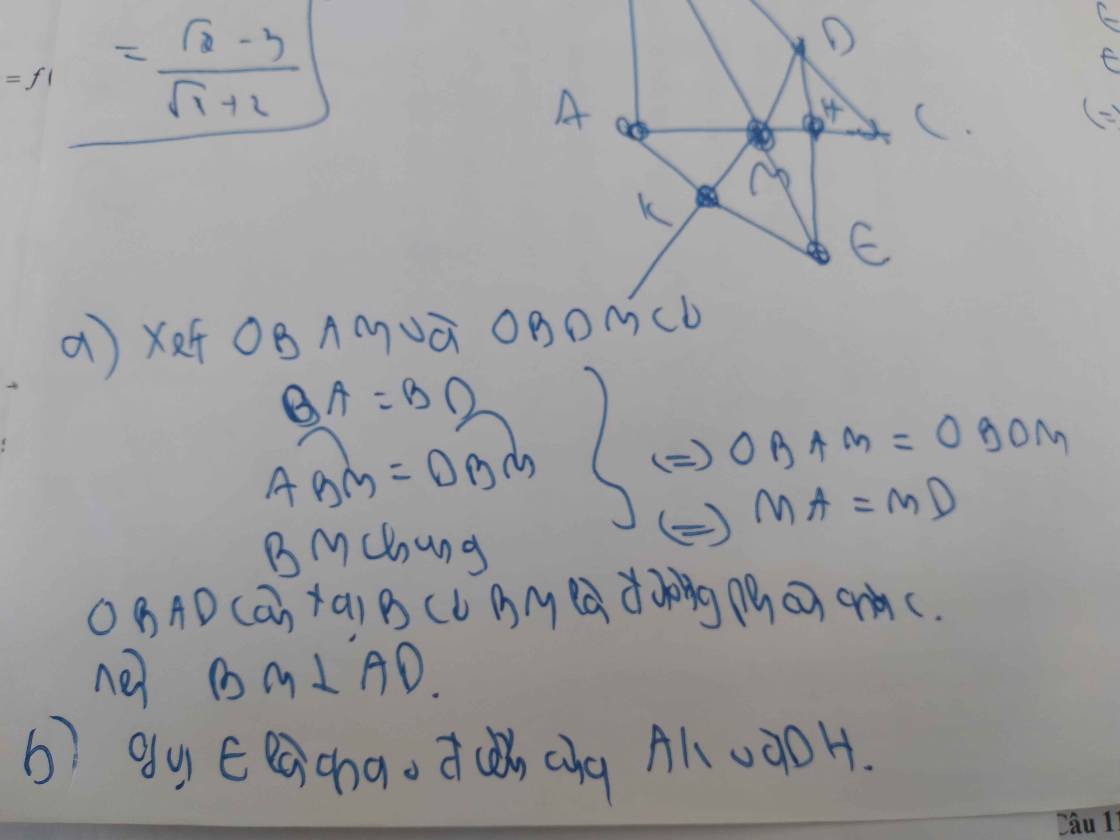
a) Do AE = AB và AD là tia phân giác của góc BAC nên tam giác ABD = tam giác AED (theo định lý cạnh góc cạnh).
Từ đó, suy ra AD vuông góc với BE (do hai tam giác cân tại D).
b) Do tam giác ABD = tam giác AED nên góc BAD = góc EAD.
Lại có góc BAF = góc EAD (cùng chắn cung BE).
Suy ra tam giác BAF = tam giác EAD (theo định lý góc cạnh góc).
Do đó, tam giác BDF = tam giác EDC.
c) Để chứng minh AI vuông góc BC, cần phải xác định rõ vị trí của điểm I. Nếu I là trung điểm của BD thì AI sẽ vuông góc với BC.
d) Do AB < AC và tam giác ABD = tam giác AED nên BD < DC.

Gọi A là biến cố "quả bóng lấy ra là số nguyên tố"
=>A={5}
=>n(A)=1
\(P\left(A\right)=\dfrac{1}{5}\)
Gọi B là biến cố "Quả bóng lấy ra ghi số chia hết cho 5"
=>B={5;10;15;20;25}
=>n(B)=5
\(P\left(B\right)=\dfrac{5}{5}=1\)
Gọi C là biến cố "Quả bóng lấy ra ghi số chia hết cho 6"
=>C=\(\varnothing\)
=>\(P\left(C\right)=0\)
a: Biến cố chắc chắn là biến cố B
b: \(P\left(A\right)=\dfrac{1}{5}\)
a, Biến cố "quả bóng lấy ra ghi số nguyên tố" là biến cố ngẫu nhiên
Biến cố " quả bóng lấy ra ghi số chia hết cho 5" là biến cố chắc chắn
Biến cố " quả bóng lấy ra ghi số chia hết cho 6" là biến cố không thể
b, Xác suất của biến cố"quả bóng lấy ra ghi số nguyên tố"là 1/5

Hình bạn tự vẽ nhé
a,Xét tam giác BAD và tam giác EDA:
AD chung
ABD=AED=90 độ( tam giác ABC vuông tại B, DE vuông góc AC)
BAD=CAD(AD là tia phân giác)
Suy ra tam giác BAD= tam giác EDA(cạnh huyền - góc nhọn)
b, Vì tam giác BAD= tam giác EDA (cmt)
Suy ra: AB=AE(2 cạnh tương ứng)
Suy ra A thuộc trung trực BE 1
Vì tam giác BAD = tam giác EDA(CMA)
Suy ra:BD=DE
Suy ra: D thuộc trung trực BE 2
Từ 1 và 2
Suy ra AD là đường trung trực BE
c,AB=AE(cmt) 3
BK=EC(gt) 4
AB+BK=AK 5
AE+EC=AC 6
Từ 3,4,5,6
Suya ra AK =AC
Suy ra tam giác AKC cân tại A 7
Mà AD là tia phân giác 8
Từ 7 và 8
Suy ra AD là đg cao tam giác AKC
Xét tam giác AKC có:
Đg cao CB( tam giác ABC vuông tại B)
Đg cao AD (cmt)
Mà AD cắt CB tại D
Suy ra D là trực tâm tam giác AKC 9
Suy ra KE là đg cao còn lại 10
Từ 9,10
Suy ra D thuộc KE
Suy ra K,D,E thg hàng

a, P(x) = 6x^3 - 3x^2 + 5x - 1
Q(x) = -6x^3 + 3x^2 - 2x + 7
b, P(x) + Q(x)
= ( 6x^3 - 3x^2 + 5x - 1 ) + ( -6x^3 +3x^2 - 2x +7 )
= 6x^3 - 3x^2 + 5x -1 + ( -6x^3 ) + 3x^2 - 2x +7
= [ 6x^3 + ( -6x^3) ] + (-3x^2 + 3x^2 ) + ( 5x - 2x ) + ( -1 +7 )
= 3x + 6
P(x) - Q(x)
= (6x^3 - 3x^2 + 5x - 1 ) - (-6x^3 + 3x^2 - 2x + 7 )
= 6x^3 - 3x^2 + 5x -1 - 6x^3 - 3x^2 + 2x - 7
= ( 6x^3 - 6x^3 ) + (-3x^2 - 3x^2 ) + ( 5x +2x ) + ( -1 - 7 )
= -6x^2 + 7x + ( -8)

Lời giải:
\(A=(\frac{-3}{4}x^2y^5).(4x^3y)=\frac{-3}{4}.4(x^2.x^3)(y^5.y)\\
=-3x^5y^6\)
Hệ số: $-3$
Phần biến: $x^5y^6$
Bậc: $5+6=11$
c.
Tại $x=-1$ và $y=1$ thì:
$A=-3(-1)^5.1^6=3$

`#3107.101107`
`1.`
`a)`
`A(x) = 2x^3 - 3x^2 + 2x + 1`
Bậc của đa thức: `3`
`B(x) = 3x^3 + 2x^2 - x - 6`
Bậc của đa thức: `3`
`b)`
Thay `x = 2` vào A:
`A(2) = 2 * 2^3 - 3 * 2^2 + 2 * 2 + 1`
`= 2^4 - 3 * 4 + 2^2 + 1`
`= 16 - 12 + 4 + 1 = 9`
Vậy, tại `x = 2` thì `A(2) = 9`
`c)`
`A(x) + B(x)`
`= 2x^3 - 3x^2 + 2x + 1 + 3x^3 + 2x^2 - x - 6`
`= (2x^3 + 3x^3) + (-3x^2 + 2x^2) + (2x - x) + (1 - 6)`
`= 5x^3 - x^2 + x - 5`
`A(x) - B(x)`
`= 2x^3 - 3x^2 + 2x + 1 - (3x^3 + 2x^2 - x - 6)`
`= 2x^3 - 3x^2 + 2x + 1 - 3x^3 - 2x^2 + x + 6`
`= (2x^3 - 3x^3) - (3x^2 + 2x^2) + (2x + x) + (1 + 6)`
`= -x^3 - 5x^2 + 3x + 7.`
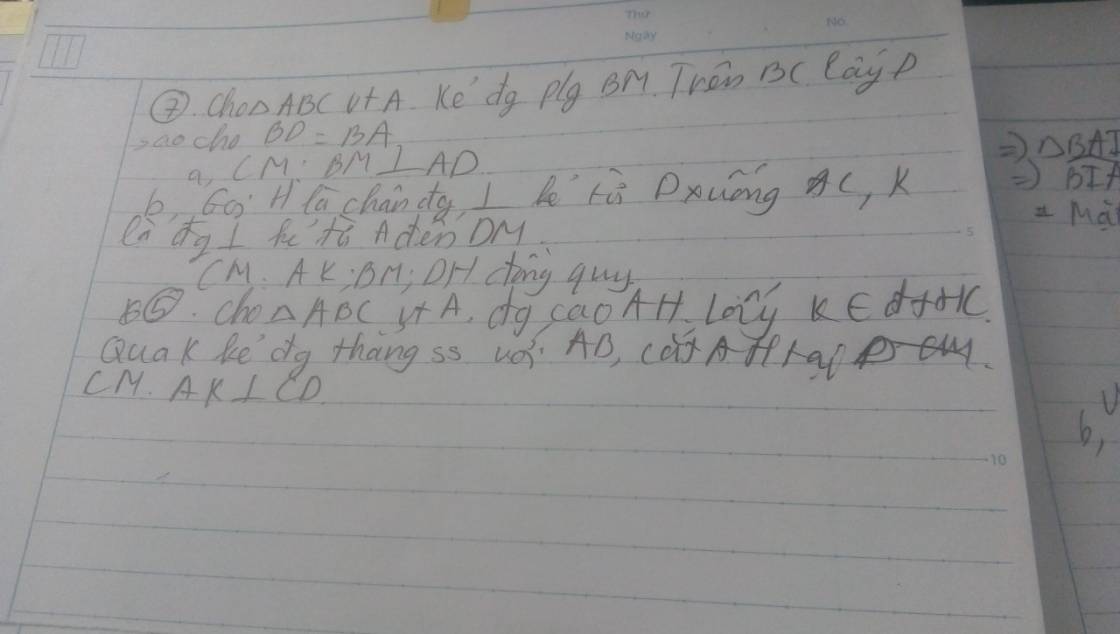

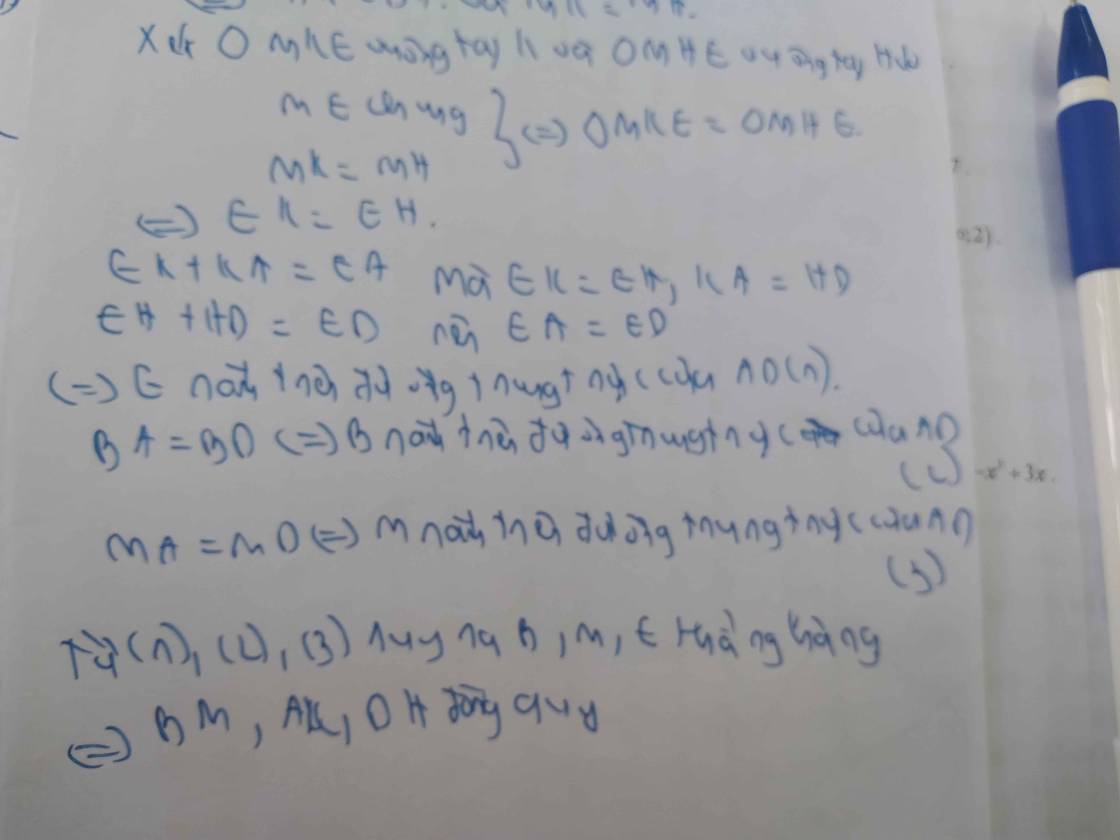
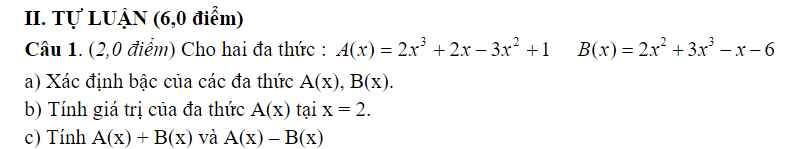
kết quả thuận lợi cho biến cố "gieo được số chấm lớn hơn 5" là: {mặt 6 chấm}
xác suất để khi "gieo được số chấm lớn hơn 5": 1/6