Đáy bé mảnh vườn đó là:

$5,4\times\dfrac23=3,6(m)$

Chiều cao mảnh vườn đó là:

$\dfrac{5,4+3,6}{2}=4,5(m)$

Diện tích mảnh vườn đó là:

$\dfrac{(5,4+3,6)\times4,5}{2}=20,25(m^2)$

Đáy bé mảnh vườn là:

\(5,4\times\dfrac{2}{3}=3,6\left(m\right)\)

Chiều cao mảnh vườn là:

\(\left(5,4+3,6\right):2=4,5\left(m\right)\)

Diện tích mảnh vườn là:

\(\left(5,4+3,6\right)\times4,5:2=20,25\left(m^2\right)\)

a. Em tự giải

b.

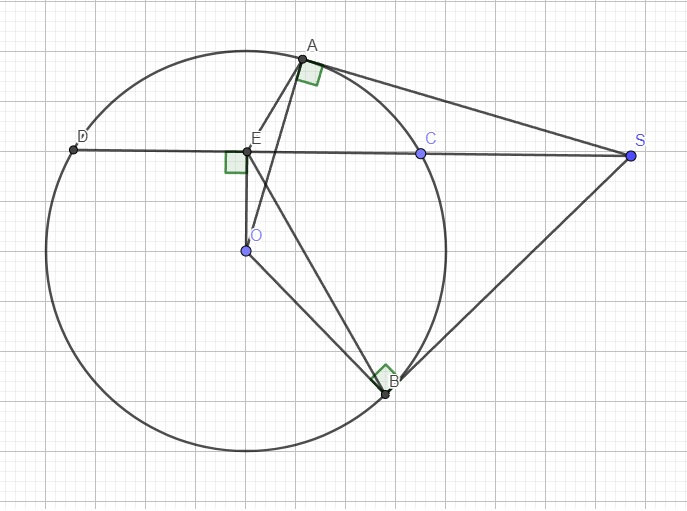
Từ câu a ta có SAOB nội tiếp

Mà \(SA=SB\) (t/c hai tiếp tuyến cắt nhau)

\(\Rightarrow\widehat{SEA}=\widehat{SEB}\) (hai góc nt chắn 2 cùng bằng nhau của đường tròn ngoại tiếp SAOB)

\(\Rightarrow\widehat{AEB}=2\widehat{SEB}\) (1)

Do E là trung điểm CD \(\Rightarrow SE\perp CD\)

\(\Rightarrow E,A,B\) cùng nhìn SO dưới 1 góc vuông nên S,A,E,B,O cùng thuộc 1 đường tròn

Hay SAEB nội tiếp

\(\Rightarrow\widehat{AEB}+\widehat{ASB}=180^0\)

Theo câu a SAOB nội tiếp \(\Rightarrow\widehat{AOB}+\widehat{ASB}=180^0\)

\(\Rightarrow\widehat{AEB}=\widehat{AOB}\) (2)

(1);(2) \(\Rightarrow\widehat{AOB}=2\widehat{SEB}\)

Gọi cạnh hình vuông của mảnh vườn là a và cạnh hình vuông của cái lều là b.
Theo đề bài, ta có:
a - b = 8 (1)
Diện tích phần mảnh vườn không tính cái lều là: (a - b)^2 = 448 (2)
Từ (1), ta có: a = b + 8. Thay vào (2), ta được:
(b + 8 - b)^2 = 448
64 = 448
b = 6
Diện tích cái lều là: b^2 = 6^2 = 36 (m^2)

là 210

\(A=\dfrac{7}{9}+\dfrac{7}{72}+\dfrac{7}{184}+\dfrac{7}{345}\)

\(A=\dfrac{2.7}{18}+\dfrac{2.7}{144}+\dfrac{2.7}{368}+\dfrac{2.7}{690}\)

\(A=2.\left(\dfrac{7}{2.9}+\dfrac{7}{9.16}+\dfrac{7}{16.23}+\dfrac{7}{23.30}\right)\)

\(A=2.\left(\dfrac{1}{2}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{16}+\dfrac{1}{16}-\dfrac{1}{23}+\dfrac{1}{23}-\dfrac{1}{30}\right)\)

\(A=2.\left(\dfrac{1}{2}-\dfrac{1}{30}\right)\)

\(A=2.\left(\dfrac{15}{30}-\dfrac{1}{30}\right)\)

\(A=\dfrac{14}{15}\)

?

Lời giải:

Vì hai số có tổng là 130 nên hai số đó là 2 số cùng lẻ hoặc 2 số cùng chẵn

Nếu hai số cần tìm cùng lẻ thì hiệu của chúng là: $8\times 2=16$ 

Số lẻ lớn $(130+16):2=73$
Số lẻ bé: $(130-16):2=57$

Nếu hai số cần tìm cùng chẵn thì hiệu của chúng là: $8\times 2+2=18$ 

Số chẵn lớn: $(130+18):2=74$

Số chẵn bé: $(130-18):2=56$

Vậy các cặp số thỏa mãn là: $(73,57)$ hoặc $(74,56)$

Lời giải:

$\frac{53}{50}$ dm³ = $1060$ cm³

Cho tam giác ABC có 3 góc nhọn nội tiếp (O;R) có 2 đường cao BE và CF cắt nhau tại H, AH cắt (O) tại K. Gọi I là trung điểm cạnh AH. Lấy điểm M thuộc cạnh KC, điểm N thuộc cạnh ME sao cho HM // BK và HN // BC. Gọi P và Q lần lượt là trung điểm các cạnh NI và NK, PE cắt MQ tại L. Đường thẳng qua L song song với AK cắt BK và SI lần lượt tại S và T. Chứng minh : Nếu $\tan B \cdot \tan C = 3$ thì L là trung điểm cạnh ST (B,C là góc tam giác ABC).