Rút gọn biểu thức (x-3)+(x-4).(x+4)-(2x-1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(x+1\right)\left(x+2\right)\left(x+3\right)-x^3-8x\left(x+2\right)=6\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+5x+6\right)-x^3-8x^2-16x=6\)
\(\Leftrightarrow x^3+6x^2+11x+6-x^3-8x^2-16x=6\)
\(\Leftrightarrow-2x^2-5x=0\)
\(\Leftrightarrow-x\left(2x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)

Bài 1:
a: Ta có: Ot là phân giác của góc xOy
=>\(\widehat{xOt}=\widehat{yOt}=\dfrac{180^0}{2}=90^0\)
=>BO\(\perp\)DC
Xét ΔOAC vuông tại A và ΔODB vuông tại D có
OA=OD
OC=OB
Do đó: ΔOAC=ΔODB
=>AC=DB(1)
Ta có: ΔOAC=ΔODB
=>\(\widehat{OAC}=\widehat{ODB}\)
mà \(\widehat{OAC}+\widehat{OCA}=90^0\)
nên \(\widehat{ODB}+\widehat{OCA}=90^0\)
=>CA\(\perp\)BD
b: Ta có;ΔOAC vuông tại O
mà OM là đường trung tuyến
nên \(OM=\dfrac{AC}{2}\)(3)
=>OM=MA=MC
Ta có: ΔOBD vuông tại O
mà ON là đường trung tuyến
nên \(ON=\dfrac{BD}{2}\)(2)
=>ON=NB=ND
Từ (1),(2),(3) suy ra OM=ON
c: NB=NO nên \(\widehat{NBO}=\widehat{NOB}\)
MA=MO
nên \(\widehat{MAO}=\widehat{MOA}\)
\(\widehat{NOM}=\widehat{NOA}+\widehat{MOA}\)
\(=\widehat{NBO}+\widehat{MAO}=\widehat{DBO}+\widehat{CAO}\)
\(=\widehat{DBO}+\widehat{ODB}=90^0\)
=>ΔNOM vuông cân tại O
=>\(\widehat{ONM}=\widehat{OMN}=45^0\)
d: Xét ΔBDC có
CA,BO là các đường cao
CA cắt BO tại A
Do đó: A là trực tâm của ΔBDC
=>DA\(\perp\)BC

\(\dfrac{2}{\left|x-2\right|+2}=\dfrac{3}{\left|6-3x\right|+1}\)
=>\(\dfrac{2}{\left|x-2\right|+2}=\dfrac{3}{3\left|x-2\right|+1}\)
=>2(3|x-2|+1)=3(|x-2|+2)
=>6|x-2|+2=3|x-2|+6
=>3|x-2|=4
=>|x-2|=4/3
=>\(\left[{}\begin{matrix}x-2=\dfrac{4}{3}\\x-2=-\dfrac{4}{3}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{10}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)

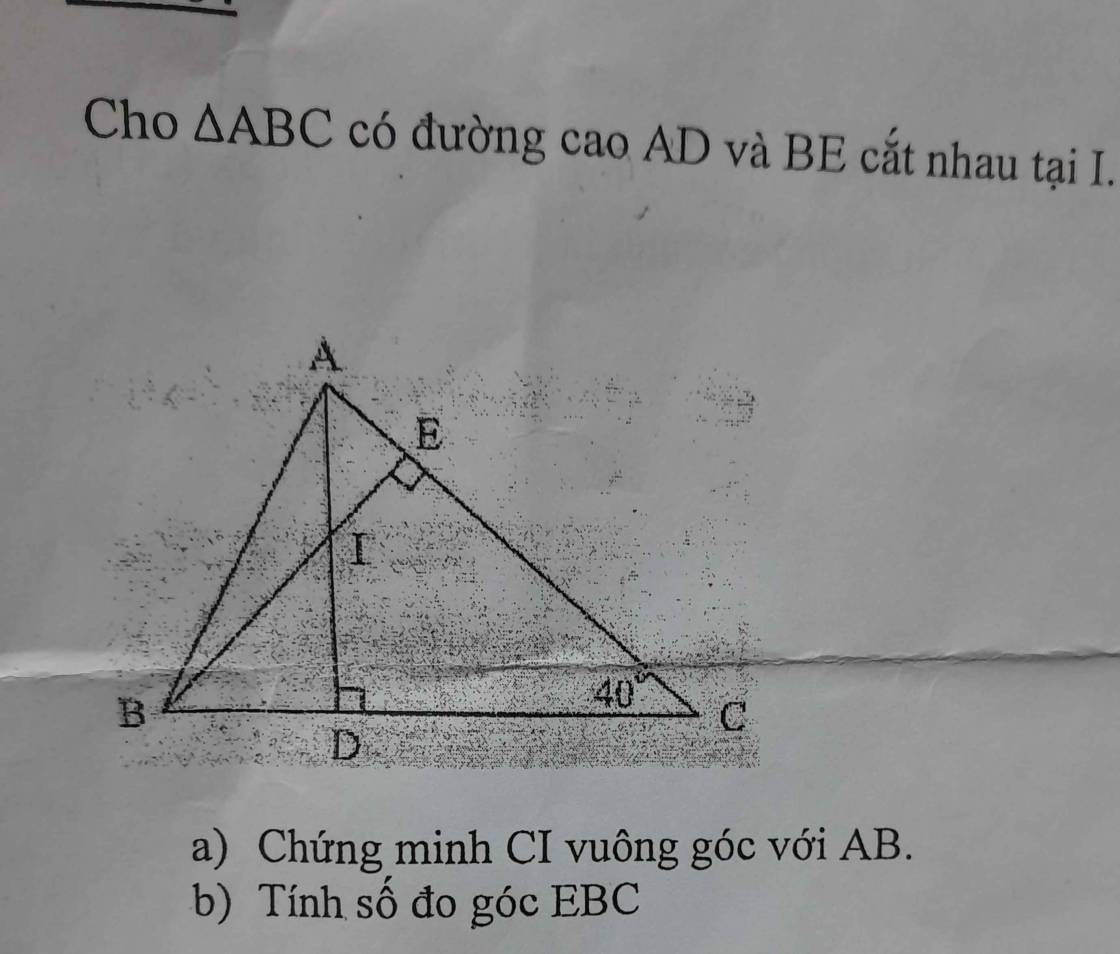
1:
a: Xét ΔABC có
AD,BE là các đường cao
AD cắt BE tại I
Do đó: I là trực tâm của ΔABC
=>CI\(\perp\)AB
b: ΔBEC vuông tại E
=>\(\widehat{EBC}+\widehat{ECB}=90^0\)
=>\(\widehat{EBC}=90^0-50^0=40^0\)
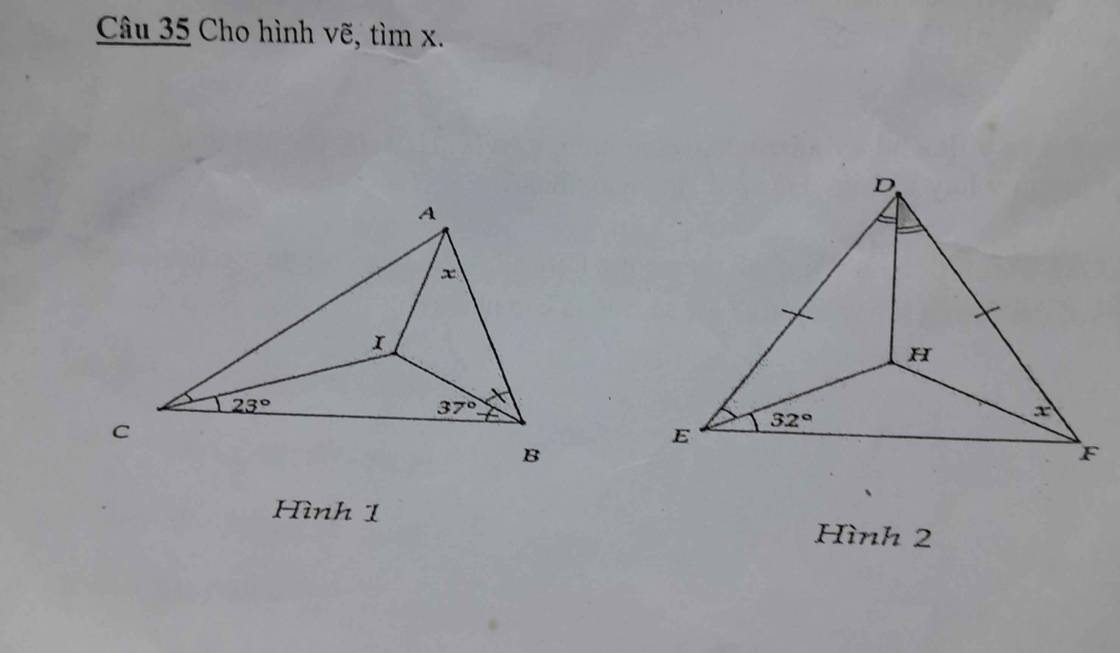
Bài 2:
a: Xét ΔABC có
CI,BI là các đường phân giác
Do đó: I là tâm đường tròn nội tiếp ΔABC
=>AI là phân giác của góc BAC
CI là phân giác của góc ACB
=>\(\widehat{ACB}=2\cdot\widehat{ICB}=46^0\)
BI là phân giác của góc ABC
=>\(\widehat{ABC}=2\cdot\widehat{ICB}=74^0\)
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+46^0+74^0=180^0\)
=>\(\widehat{BAC}=60^0\)
=>\(x=\dfrac{\widehat{BAC}}{2}=30^0\)
b: Xét ΔDEF có
EH,DH là các đường phân giác
Do đó: H là tâm đường tròn nội tiếp ΔDEF
=>FH là phân giác của góc DFE
EH là phân giác của góc DEF
=>\(\widehat{DEF}=2\cdot\widehat{HEF}=64^0\)
Xét ΔDEF có DE=DF
nên ΔDEF cân tại D
=>\(\widehat{DFE}=\widehat{DEF}=64^0\)
=>\(x=\dfrac{64^0}{2}=32^0\)

\(x^2+7⋮x-2\)
=>\(x^2-4+11⋮x-2\)
=>\(11⋮x-2\)
=>\(x-2\in\left\{1;-1;11;-11\right\}\)
=>\(x\in\left\{3;1;13;-9\right\}\)

\(P\left(x\right)=-x^4+4x^2-x\left(x^2-x^3\right)+1\)
\(=-x^4+4x^2-x^3+x^4+1\)
\(=-x^3+4x^2+1\)
=>Bậc là 3

18 người thợ xây xây xong ngôi nhà trong:
\(30\cdot12:18=360:18=20\left(ngày\right)\)

a: Xét ΔMAB và ΔMCD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔMAB=ΔMCD
b: Xét ΔCBD có
CM,DN là các đường trung tuyến
CM cắt DN tại G
Do đó: G là trọng tâm của ΔCBD
c: Bạn ghi lại đề đi bạn

\(A\left(x\right)=-\dfrac{6x}{2}-5x-4=-3x-5x-4=-8x-4\)
\(A\left(-2\right)=-8\cdot\left(-2\right)-4=16-4=12\)

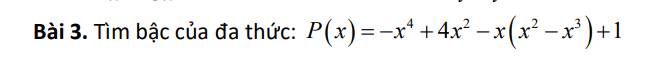
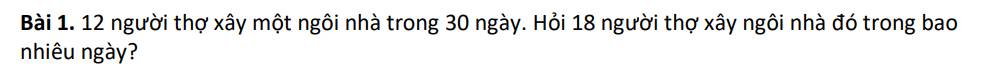
\(\left(x-3\right)+\left(x-4\right)\left(x+4\right)-\left(2x-1\right)\)
\(=x-3+x^2-16-2x+1\)
\(=x^2-x-18\)
\(\left(x-3\right)+\left(x-4\right).\left(x+4\right)-\left(2x-1\right)\)
\(=x-3+x.x+4x-4x+16-2x+1\)
\(=x-3+x^2-16-2x+1\)
\(=x^2+\left(x-2x\right)+\left(-3-16+1\right)\)
\(=x^2-x-18\)