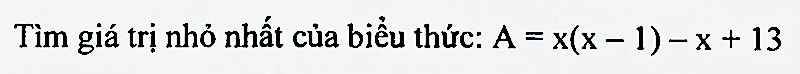
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: A>3
mà 123456789 có tổng các chữ số chia hết cho 3 nên chia hết cho 3
và 1.2.3.4.5.6.7.8.9 cũng chia hết cho 3
Vậy A chia hết cho 3 (tức A chia hết cho một số khác 1 và chính nó) nên A là hợp số
b) Ta có: B>3
B=1! + 2! + .... + 2021!
= 1 + 1.2 + 3! +...+ 2021!
= 3 + 3! +... + 2021!
vì 3 chia hết cho 3 và các giai thừa còn lại trong B đều có chứ thừa số 3 nên chia hết cho 3
Vậy B chia hết cho 3 (tức B chia hết cho một số khác 1 và chính nó) nên B là hợp số

Hoặc bạn có thể tham gia các cuộc thi do cô Thương Hoài tổ chức
Cách kiếm GP giống như khi bạn kiếm SP thôi, quan trọng là được các thầy cô, anh chị CTV tick.
Coin thì bạn có thể tham gia các Mini Games ở mục câu hỏi hay để được thưởng hoặc có nhiều GP để được lên BXH tùy theo mức độ nhất, nhì bạn sẽ có 400 xu hoặc 300 xu. 1 coin = 10 xu

Số quả trứng bán lần 1:
60 . 3/4 = 45 (quả)
Số quả trứng còn lại:
60 - 45 = 15 (quả)
Số quả trứng bán lần 2:
15 × 1/3 = 5 (quả)
Số quả trứng bán lần 3:
15 - 5 = 10 (quả)


Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{a}=k\)(k<>0)
=>\(\left\{{}\begin{matrix}d=a\cdot k\\c=d\cdot k=a\cdot k\cdot k=ak^2\\b=ck=ak^3\\a=bk=ak^4\end{matrix}\right.\)
\(a=ak^4\)
=>\(ak^4-a=0\)
=>\(a\left(k^4-1\right)=0\)
=>\(k^4-1=0\)
=>\(\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\)
\(M=\dfrac{3a+b}{5b-d}+\dfrac{2b+3c}{2d-b}\)
\(=\dfrac{3\cdot ak^4+ak^3}{5\cdot ak^3-ak}+\dfrac{2\cdot ak^3+3\cdot ak^2}{2\cdot ak-ak^3}\)
\(=\dfrac{ak^3\left(3k+1\right)}{ak\left(5k^2-1\right)}+\dfrac{ak^2\left(2k+3\right)}{ak\left(2-k^2\right)}\)
\(=\dfrac{k^2\left(3k+1\right)}{5k^2-1}+\dfrac{k\left(2k+3\right)}{2-k^2}\)
TH1: k=1
=>\(M=\dfrac{1^2\left(3\cdot1+1\right)}{5\cdot1^2-1}+\dfrac{1\left(2\cdot1+3\right)}{2-1^2}=\dfrac{4}{4}+\dfrac{5}{1}=6\)
TH2: k=-1
=>\(M=\dfrac{\left(-1\right)^2\cdot\left(-3+1\right)}{5\cdot\left(-1\right)^2-1}+\dfrac{\left(-1\right)\left(2\cdot\left(-1\right)+3\right)}{2-\left(-1\right)^2}\)
\(=\dfrac{-2}{4}+\dfrac{1}{1}=-\dfrac{1}{2}+1=\dfrac{1}{2}\)

=(8/9+8/10+8/11+...+8/100):(1/5x1/9+1/5x1/10+...+1/5x1/100)
=8(1/9+1/10+1/11+...+1/100):1/5(1/9+1/10+...+1/100)
=8x5=40

\(\left(\dfrac{1}{2}+1\right)\cdot\left(\dfrac{1}{3}+1\right)\cdot\left(\dfrac{1}{4}+1\right)\cdot...\cdot\left(\dfrac{1}{99}+1\right)\\ =\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot\dfrac{5}{4}\cdot...\cdot\dfrac{100}{99}\\ =\dfrac{3\cdot4\cdot5\cdot...\cdot100}{2\cdot3\cdot4\cdot.....\cdot99}\\ =\dfrac{100}{2}=50\)
\(A=x(x-1)-x+13\\=x^2-x-x+13\\=(x^2-2x+1)+12\\=(x-1)^2+12\)
Ta thấy: \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^2+12\ge12\forall x\Rightarrow A\ge12\forall x\)
Dấu \("="\) xảy ra khi: \(x-1=0\Leftrightarrow x=1\)
Vậy \(Min_A=12\) tại \(x=1\).