Cho tam giác ABC cân tại A. Kẻ BH AC CK AB ⊥ ⊥ ; ( H AC ; K AB ).
a) Chứng minh tam giác AKH là tam giác cân
b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của BIC .
c) Chứng minh: HK BC // .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
\(\widehat{ABE}=\widehat{DBE}\)
Do đó: ΔBAE=ΔBDE
b: Xét ΔBFC có
BH là đường cao
BH là đường phân giác
Do đó: ΔBFC cân tại B
c: Xét ΔBFC có
BH,CA là các đường cao
BH cắt CA tại E
Do đó: E là trực tâm của ΔBFC
=>FE\(\perp\)BC
mà ED\(\perp\)BC
nên F,E,D thẳng hàng

\(A\left(x\right)=2x^2-4x+7\)
\(B\left(x\right)=5x^2+2x+3\)
a/ \(A\left(x\right)+B\left(x\right)=\left(2x^2-4x+7\right)+\left(5x^2+2x+3\right)\)
\(=2x^2-4x+7+5x^2+2x+3\)
\(=7x^2-2x+10\)
b/ \(A\left(x\right)-B\left(x\right)=\left(2x^2-4x+7\right)-\left(5x^2+2x+3\right)\)
\(=2x^2-4x+7-5x^2-2x-3\)
\(=-3x^2-6x+4\)
a, Ta có: \(A\left(x\right)+B\left(x\right)=2x^2-4x+7+5x^2+2x+3\\ \Rightarrow A\left(x\right)+B\left(x\right)=7x^2-2x+10\)
Vậy...
b, Ta có :\(A\left(x\right)-B\left(x\right)=2x^2-4x+7-5x^2-2x-3\\ \Rightarrow A\left(x\right)-B\left(x\right)=-3x^2-6x+4.\)
Vậy...

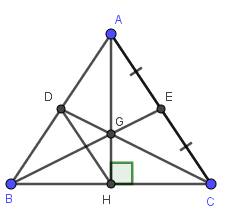
a) Do \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow AB=AC\)
Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:
\(AB=AC\left(cmt\right)\)
\(AH\) là cạnh chung
\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)
b) \(\Delta ABC\) cân tại A (gt)
\(AH\) là đường cao của \(\Delta ABC\) (gt)
\(\Rightarrow AH\) cũng là đường phân giác, đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)
\(\Rightarrow\widehat{DAH}=\widehat{HAC}\)
Do \(HD\) // \(AC\) (gt)
\(\Rightarrow\widehat{AHD}=\widehat{HAC}\)
Mà \(\widehat{DAH}=\widehat{HAC}\left(cmt\right)\)
\(\Rightarrow\widehat{AHD}=\widehat{DAH}\)
\(\Rightarrow\Delta AHD\) cân tại D
\(\Rightarrow AD=DH\)
c) Do \(\Delta ABC\) cân tại A (gt)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{DBH}=\widehat{ACB}\)
Do \(HD\) // \(AC\) (gt)
\(\Rightarrow\widehat{DHB}=\widehat{ACB}\) (đồng vị)
Mà \(\widehat{DBH}=\widehat{ACB}\left(cmt\right)\)
\(\Rightarrow\widehat{DHB}=\widehat{DBH}\)
\(\Rightarrow\Delta BHD\) cân tại D
\(\Rightarrow DH=BD\)
Mà \(DH=AD\left(cmt\right)\)
\(\Rightarrow AD=BD\)
\(\Rightarrow D\) là trung điểm của AB
\(\Rightarrow CD\) là đường trung tuyến của \(\Delta ABC\)
Lại có \(AH\) là đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow G\) là trọng tâm của \(\Delta ABC\)
Do \(E\) là trung điểm của AC (gt)
\(\Rightarrow BE\) là đường trung tuyến của \(\Delta ABC\)
Mà \(G\) là trọng tâm của \(\Delta ABC\) (cmt)
\(\Rightarrow B,G,E\) thẳng hàng
\(\Rightarrow AH\) cũng là đường trung tuyến


\(2x^3-4x^2+3x+a-10=2x^3-4x^2+3x-6+a-4\)
\(=\left(2x^3-4x^2\right)+\left(3x-6\right)+a-4\)
\(=2x^2\left(x-2\right)+3\left(x-2\right)+a-4\)
\(\Rightarrow\left(2x^3-4x^2+3x+a-10\right):\left(x-2\right)\)
\(=\left[2x^2\left(x-2\right)+3\left(x-2\right)+a-4\right]:\left(x-2\right)\)
\(=2x^2+3+\dfrac{a-4}{x-2}\)
Để đa thức đã cho chia hết cho \(x-2\) thì \(a-4=0\)
\(\Rightarrow a=4\)

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: \(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACE}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
=>AD=AE
vẽ hình hộ mình nhé đang cần gấp
nhớ tích cho tui nhe