cho tam giac ABC deu tren
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số quyển tập ba lớp 7A,7B,7C quyên góp được lần lượt là a(quyển),b(quyển),c(quyển)
(Điều kiện: \(a,b,c\in Z^+\))
Số quyển tập ba lớp quyên góp được lần lượt tỉ lệ với 7;3;4 nên \(\dfrac{a}{7}=\dfrac{b}{3}=\dfrac{c}{4}\)
Tổng số quyển tập ba lớp quyên góp được là 420 nên a+b+c=420
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{7}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{7+3+4}=\dfrac{420}{14}=30\)
=>\(a=30\cdot7=210\left(nhận\right);b=3\cdot30=90\left(nhận\right);c=4\cdot30=120\left(nhận\right)\)
vậy: số quyển tập ba lớp 7A,7B,7C quyên góp được lần lượt là 210(quyển),90(quyển),120(quyển)

Gọi số tiền đơn vị 1,2,3 đóng góp lần lượt là a(triệu),b(triệu),c(triệu)
(Điều kiện: a>0; b>0; c>0)
Số tiền đóng góp của 3 đơn vị lần lượt tỉ lệ với 3;5;8 nên \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}\)
Tổng số tiền lãi là 256 triệu nên a+b+c=256
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{8}=\dfrac{a+b+c}{3+5+8}=\dfrac{256}{16}=16\)
=>\(a=16\cdot3=48;b=16\cdot5=80;c=16\cdot8=128\)
vậy: Số tiền ba đơn vị đóng góp lần lượt là 48 triệu; 80 triệu; 128 triệu

\(4x^2+4x=2\)
=>\(2x^2+2x=1\)
=>\(2x^2+2x-1=0\)
\(\Delta=2^2-4\cdot2\cdot\left(-1\right)=4+8=12>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-2-\sqrt{12}}{2\cdot2}=\dfrac{-2-2\sqrt{3}}{4}=\dfrac{-1-\sqrt{3}}{2}\\x_2=\dfrac{-1+\sqrt{3}}{2}\end{matrix}\right.\)

\(E\left(x\right)=2x+1=0\)
\(\Rightarrow2x=-1\)
\(\Rightarrow x=-\dfrac{1}{2}\)
Vậy \(x=-\dfrac{1}{2}\) là nghiệm của đa thức
\(E\left(x\right)=0\Rightarrow2x+1=0\)
\(\Rightarrow2x=-1\)
\(\Rightarrow x=\dfrac{-1}{2}\)
Vậy...

a: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
Do đó: ΔBAH=ΔBDH
b: ΔBAH=ΔBDH
=>\(\widehat{ABH}=\widehat{DBH}\)
Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=30^0\)
Xét ΔEDC vuông tại D có \(sinECD=\dfrac{ED}{EC}\)
=>\(\dfrac{EA}{EC}=sin30=\dfrac{1}{2}\)
=>EC=2AE

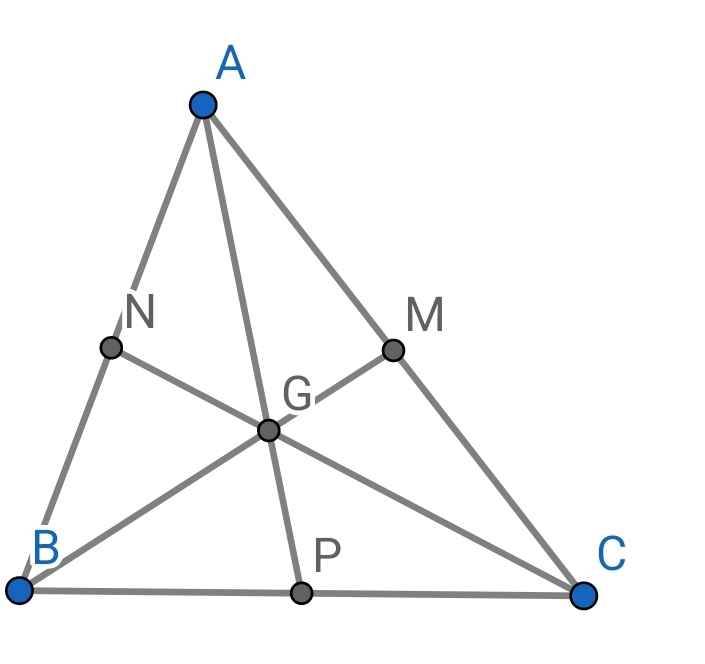
Do BM và CN là hai đường trung tuyến cắt nhau tại G (gt)
G là trọng tâm của ABC
AG là đường trung tuyến thứ ba
Mà AG cắt BC tại P
AG = 2/3 . AP = 2/3 . 6 = 4 (cm)
Chọn A

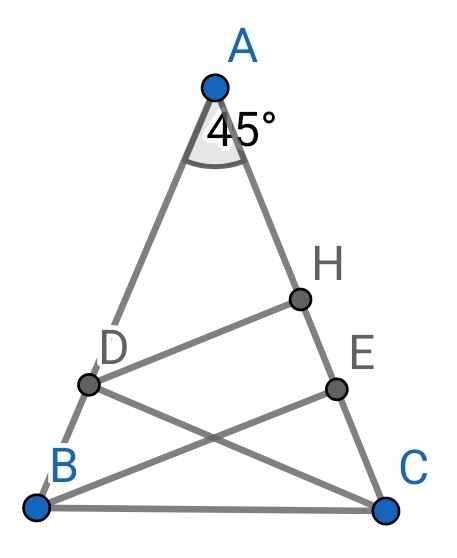
a) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2
= (180⁰ - 45⁰) : 2
= 67,5⁰
Do ∠ABC = ∠ACB > ∠BAC (67,5⁰ = 67,5⁰ > 45⁰)
⇒ AC = AB > BC
b) Do ∠ABC = ∠ACB (cmt)
⇒ ∠DBC = ∠ECB
Xét ∆BCD và ∆CBE có:
BD = CE (gt)
∠DBC = ∠ECB (cmt)
BC là cạnh chung
⇒ ∆BCD = ∆CBE (c-g-c)
⇒ ∠BDC = ∠CEB (hai góc tương ứng)

a: Xét ΔMHN vuông tại H và ΔMHP vuông tại H có
MN=MP
MH chung
Do đó: ΔMHN=ΔMHP
b: Xét ΔIGM và ΔIEN có
IG=IE
\(\widehat{GIM}=\widehat{EIN}\)(hai góc đối đỉnh)
IM=IN
Do đó: ΔIGM=ΔIEN
=>\(\widehat{IGM}=\widehat{IEN}\)
=>MG//EN
anh ở vùng quê khu nghèo khó đó đeo có píc cà bôn