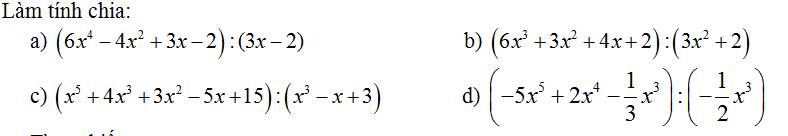
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Độ dài quãng đường ô tô đi được là:
60x(km)
b: Trong 30 giây đập nước đó xả ra được:
30x(m3)

\(\left(5x^2-2x+1\right)\left(x-2\right)-3x\left(x+1\right)+7\)
\(=5x^3-10x^2-2x^2+4x+x-2-3x^2-3x+7\)
\(=5x^3-15x^2+2x+5\)

ΔDBA vuông cân tại D
=>\(\widehat{DAB}=45^0\)
Vì \(\widehat{BAD}< \widehat{BAC}\)
nên tia AD nằm giữa hai tia AB,AC
=>\(\widehat{BAD}+\widehat{DAC}=\widehat{BAC}\)
=>\(\widehat{DAC}+45^0=90^0\)
=>\(\widehat{DAC}=45^0\)
Vì AD nằm giữa hai tia AB,AC
mà \(\widehat{BAD}=\widehat{CAD}\left(=45^0\right)\)
nên AD là tia phân giác của góc BAC

a: Độ dài quãng đường người đó đi bộ là 5x(km)
Độ dài quãng đường người đó đi bằng ô tô là 55y(km)
Tổng độ dài quãng đường là 5x+55y(km)
b: Độ dài mỗi đoạn là \(\dfrac{a}{9}\left(m\right)\)

a: Sửa đề: Cho ΔDEF
Xét ΔDEF có DE<DF
mà \(\widehat{DFE};\widehat{DEF}\) lần lượt là góc đối diện của các cạnh DE,DF
nên \(\widehat{DFE}< \widehat{DEF}\)
b: Xét ΔDEF có
DN,EM là các đường trung tuyến
DN cắt EM tại G
Do đó: G là trọng tâm của ΔDEF

\(2n^2-n+2⋮2n+1\)
=>\(2n^2+n-2n-1+3⋮2n+1\)
=>\(3⋮2n+1\)
=>\(2n+1\in\left\{1;-1;3;-3\right\}\)
=>\(n\in\left\{0;-1;1;-2\right\}\)

Thể tích của của thùng là:
40x25x30=30000(cm3)
Thời gian hết lượng nước là:
30000:1500=20(giờ)

a: A(x)+B(x)
\(=-x^3+2x-15-5x^3+x^2-4x+7\)
\(=-6x^3+x^2-2x-8\)
b: A(x)+C(x)
\(=-x^3+2x-15+3x^3-7x^2-4\)
\(=2x^3-7x^2+2x-19\)
c: A(x)-B(x)
\(=-x^3+2x-15+5x^3-x^2+4x-7\)
\(=4x^3-x^2+6x-22\)
d: B(x)-C(x)
\(=-5x^3+x^2-4x+7-3x^3+7x^2+4\)
\(=-8x^3+8x^2-4x+11\)
e: B(x)-A(x)+C(x)
\(=-5x^3+x^2-4x+7+x^3-2x+15+3x^3-7x^2-4\)
\(=-x^3-6x^2-6x+18\)
f: C(x)-B(x)-A(x)
\(=3x^3-7x^2-4+x^3-2x+15+5x^3-x^2+4x-7\)
\(=9x^3-8x^2+2x+4\)

a: M(x)-2N(x)
\(=x^3+2x^2+1-2\left(x^2-2x+3\right)\)
\(=x^3+2x^2+1-2x^2+4x-6\)
\(=x^3+4x-5\)
b: 1/2M(x)+N(x)
\(=\dfrac{1}{2}\left(x^3+2x^2+1\right)+x^2-2x+3\)
\(=\dfrac{1}{2}x^3+x^2+\dfrac{1}{2}+x^2-2x+3\)
\(=\dfrac{1}{2}x^3+2x^2-2x+\dfrac{7}{2}\)
c: M(x)-N(x)
\(=x^3+2x^2+1-x^2+2x-3\)
\(=x^3+x^2+2x-2\)
N(x)-M(x)
\(=-\left(x^3+x^2+2x-2\right)\)
\(=-x^3-x^2-2x+2\)
M(x)+N(x)
\(=x^3+2x^2+1+x^2-2x+3\)
\(=x^3+3x^2-2x+4\)


a: \(\dfrac{6x^4-4x^2+3x-2}{3x-2}\)
\(=\dfrac{2x^2\left(3x-2\right)+3x-2}{3x-2}=2x^2+1\)
b: \(\dfrac{6x^3+3x^2+4x+2}{3x^2+2}\)
\(=\dfrac{\left(6x^3+4x\right)+\left(3x^2+2\right)}{3x^2+2}\)
\(=\dfrac{2x\cdot\left(3x^2+2\right)+\left(3x^2+2\right)}{3x^2+2}=2x+1\)
c: \(\dfrac{x^5+4x^3+3x^2-5x+15}{x^3-x+3}\)
\(=\dfrac{x^5-x^3+3x^2+5x^3-5x+15}{x^3-x+3}\)
\(=\dfrac{x^2\left(x^3-x+3\right)+5\left(x^3-x+3\right)}{x^3-x+3}=x^2+5\)
d: \(\dfrac{-5x^5+2x^4-\dfrac{1}{3}x^3}{-\dfrac{1}{2}x^3}=\dfrac{5x^5}{\dfrac{1}{2}x^3}-\dfrac{2x^4}{\dfrac{1}{2}x^3}+\dfrac{\dfrac{1}{3}x^3}{\dfrac{1}{2}x^3}\)
\(=10x^2-4x+\dfrac{2}{3}\)