Bài 5: (1 điểm) Tìm giá trị nhỏ nhất của các biểu thức $B=3 x^2+3 y^2+z^2+5 x y-3 y z-3 x z-2 x-2 y+3 $.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔMAB có MD là phân giác
nên \(\dfrac{AD}{DB}=\dfrac{AM}{MB}=\dfrac{AM}{MC}\left(1\right)\)
Xét ΔMAC có ME là phân giác
nên \(\dfrac{AE}{EC}=\dfrac{AM}{MC}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
Xét ΔABC có \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
nên DE//BC
b: Xét ΔABM có DI//BM
nên \(\dfrac{DI}{BM}=\dfrac{AI}{AM}\left(3\right)\)
Xét ΔAMC có IE//MC
nên \(\dfrac{IE}{MC}=\dfrac{AI}{AM}\left(4\right)\)
Từ (3),(4) suy ra \(\dfrac{DI}{BM}=\dfrac{IE}{MC}\)
mà BM=MC(M là trung điểm của BC)
nên DI=IE
=>I là trung điểm của DE

\(H\left(x\right)=x^2+y^2-xy+x+y+1\)
\(\Rightarrow12H\left(x\right)=12\left(x^2+y^2-xy-x+y+1\right)\)
\(\Rightarrow12H\left(x\right)=12x^2+12y^2-12xy-12x+12y+12\)
\(\Rightarrow12H\left(x\right)=\left(12x^2-12xy+3y^2-12x+6y+3\right)+\left(9y^2+6y+9\right)\)
\(\Rightarrow12H\left(x\right)=3\left(4x^2-4xy+y^2-4x+2y+1\right)+\left(9y^2+6y+1\right)+8\)
\(\Rightarrow12H\left(x\right)=3\left[\left(2x\right)^2+y^2+1^2-2\cdot2x\cdot y-2\cdot2x\cdot1+2\cdot y\cdot1\right]+\left[\left(3y\right)^2+2\cdot3y\cdot1+1^2\right]+8\)
\(\Rightarrow12H\left(x\right)=3\left(2x-y-1\right)^2+\left(3y+1\right)^2+8\)
\(\Rightarrow H\left(x\right)=\dfrac{3\left(2x-y-1\right)^2+\left(3y+1\right)^2+8}{12}=\dfrac{\left(2x-y-1\right)^2}{4}+\dfrac{\left(3y+1\right)^2}{12}+\dfrac{2}{3}\)
Ta có: \(\left\{{}\begin{matrix}\dfrac{\left(2x-y-1\right)^2}{4}\ge0\forall x,y\\\dfrac{\left(3y+1\right)^2}{12}\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow H\left(x\right)=\dfrac{\left(2x-y-1\right)^2}{4}+\dfrac{\left(3y+1\right)^2}{12}+\dfrac{2}{3}\ge\dfrac{2}{3}\forall x,y\)
Dấu "=" xảy ra:
\(\left\{{}\begin{matrix}2x-y-1=0\\3y+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{1}{3}-1=0\\y=-\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy: ...

a) Viết một số ngẫu nhiên có 2 hoặc 3 chữ số nhỏ hơn 200 các số có thể viết được là:
\(10;11;12;13;...;199;200\)
Số cách viết là:
\(\left(200-10\right):1+1=191\) (cách)
b) Các số chia hết cho 2 và 5 có 2 hoặc 3 chữ số nhỏ hơn 200 là:
\(10;20;30;...;200\)
Có: \(\left(200-10\right):10+1=20\) (số)
Xác xuất xảy ra biến cố là: \(P=\dfrac{20}{191}\)
Có 11 số tự nhiên có 2 hoặc 3 chữ số được viết ra là bình phương của một số tự nhiên nhỏ hơn 200 là: \(16;25;36;49;64;81;100;121;144;169;196\)
Xác xuất xảy ra biến cố là:
\(P=\dfrac{11}{191}\)
a) Các số có thể viết:
10; 11; 12; ...; 198; 199
Số cách viết:
199 - 10 + 1 = 190 (cách)
b) *) Gọi A là biến cố "Số tự nhiên được viết ra là số chia hết cho 2 và 5"
Các số chia hết cho 2 và 5 có thể viết:
10; 20; 30; ...; 180; 190
Số các số đó:
(190 - 10) : 10 + 1 = 19 (số)
⇒ P(A) = 19/190 = 1/10
*) Gọi B là biến cố "Số tự nhiên được viết ra là bình phương của một số tự nhiên"
Các số là bình phương của một số tự nhiên nhỏ hơn 200:
4²; 5²; 6²; 7²; 8²; 9²; 10²; 11²; 12²; 13²; 14²
Số các số đó là:
14 - 4 + 1 = 11 (số)
⇒ P(B) = 11/190

câu a: Ta có BD là đường phân giác của ΔABC
⇒ \(\dfrac{DA}{DC}=\dfrac{BA}{BC}\)
\(\Leftrightarrow\dfrac{DA+DC}{DC}=\dfrac{BA+BC}{BC}\)
ta có AC = CD + AD, mà AC = AB = 15CM
\(\dfrac{15}{DC}=\dfrac{15+10}{10}\\ \dfrac{15}{CD}=\dfrac{25}{10}\\ \Rightarrow CD=\dfrac{15\cdot10}{25}=6\left(cm\right)\)
⇒ DA = AC - CD = 15 - 6 = 9 (cm)
câu b: ta có: BD ⊥ BE nên BE là đường phân giác của góc ngoài tại đỉnh B
\(\Rightarrow\dfrac{BC}{AB}=\dfrac{EC}{EA}=\dfrac{EC}{EC+AC}=\dfrac{EC}{EC+15}=\dfrac{10}{15}=\dfrac{2}{3}\)
\(\dfrac{EC}{EC+15}=\dfrac{2}{3}\Rightarrow3EC=2EC+30\\ \Rightarrow3EC-2EC=30\\ \Rightarrow EC=30\left(cm\right)\)

Nếu p;q cùng lẻ \(\Rightarrow p^q.q^p\) lẻ
Trong khi đó \(2p+q+1\) và \(2q+p+1\) chẵn \(\Rightarrow\left(2p+q+1\right)\left(2q+p+1\right)\) chẵn (ktm)
\(\Rightarrow\) Trong 2 số p và q phải có ít nhất 1 số chẵn.
Do vai trò của p và q là như nhau, ko mất tính tổng quát, giả sử q chẵn
\(\Rightarrow q=2\Rightarrow p^2.2^p=\left(2p+3\right)\left(p+5\right)\)
\(\Rightarrow p^2.2^p=2p^2+13p+15\)
- Với \(p=2\) ko thỏa mãn
- Với \(p=3\) thỏa mãn
- Với \(p>3\Rightarrow p\ge5\)
\(\Rightarrow p^2.2^p\ge p^2.2^5=32p^2\)
\(\Rightarrow2p^2+13p+15\ge32p^2\)
\(\Rightarrow2p^2+13p\left(p-1\right)+15\left(p^2-1\right)\le0\) (vô lý do \(p\ge5\Rightarrow\left\{{}\begin{matrix}p^2>0\\p-1>0\\p^2-1>0\end{matrix}\right.\))
Vậy \(\left(p;q\right)=\left(2;3\right);\left(3;2\right)\)


Ta có: \(D\left(x\right)=2x^2+3y^2+4z^2-2\left(x+y+z\right)+2\)
\(=2x^2+3y^2+4z^2-2x-2y-2z+2\)
\(=\left(2x^2-2x\right)+\left(3y^2-2y\right)+\left(4z^2-2z\right)+2\)
\(=2\left(x^2-x\right)+3\left(y^2-\dfrac{2}{3}y\right)+4\left(z^2-\dfrac{1}{2}z\right)+2\)
\(=2\left[x^2-2\cdot x\cdot\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{1}{2}\right)^2\right]+3\left[y^2-2\cdot y\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2-\left(\dfrac{1}{3}\right)^2\right]+4\left[z^2-2\cdot z\cdot\dfrac{1}{4}+\left(\dfrac{1}{4}\right)^2-\left(\dfrac{1}{4}\right)^2\right]+2\)\(=2\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}+3\left(y-\dfrac{1}{3}\right)^2-\dfrac{1}{3}+4\left(z-\dfrac{1}{4}\right)^2-\dfrac{1}{4}+2\)
\(=2\left(x-\dfrac{1}{2}\right)^2+3\left(y-\dfrac{1}{3}\right)^2+4\left(z-\dfrac{1}{4}\right)^2+\dfrac{11}{12}\)
Mà: \(\left\{{}\begin{matrix}2\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\\3\left(y-\dfrac{1}{3}\right)^2\ge0\forall y\\4\left(y-\dfrac{1}{4}\right)^2\ge0\forall z\end{matrix}\right.\)
\(\Rightarrow D\left(x\right)=2\left(x-\dfrac{1}{2}\right)^2+3\left(y-\dfrac{1}{3}\right)^2+4\left(z-\dfrac{1}{4}\right)^2+\dfrac{11}{12}\ge\dfrac{11}{12}\forall x,y,z\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x-\dfrac{1}{2}=0\\y-\dfrac{1}{3}=0\\z-\dfrac{1}{4}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\\z=\dfrac{1}{4}\end{matrix}\right.\)
Vậy: ...
D(x)=2(x2−x)+(3y2−2y)+(4z2−2z)+2
=2(�2−�+14)+3(�2−23�+19)+[(2�)2−2�+14]+2−12−13−14=2(x2−x+41)+3(y2−32y+91)+[(2z)2−2z+41]+2−21−31−41
=2(�−12)2+3(�−13)2+(2�−12)2+112≥112=2(x−21)2+3(y−31)2+(2z−21)2+211≥211
Vậy giá trị nhỏ nhất của �D là: 112211 tại (�,�,�)=(12;13;14)(x,y,z)=(21;31;41).

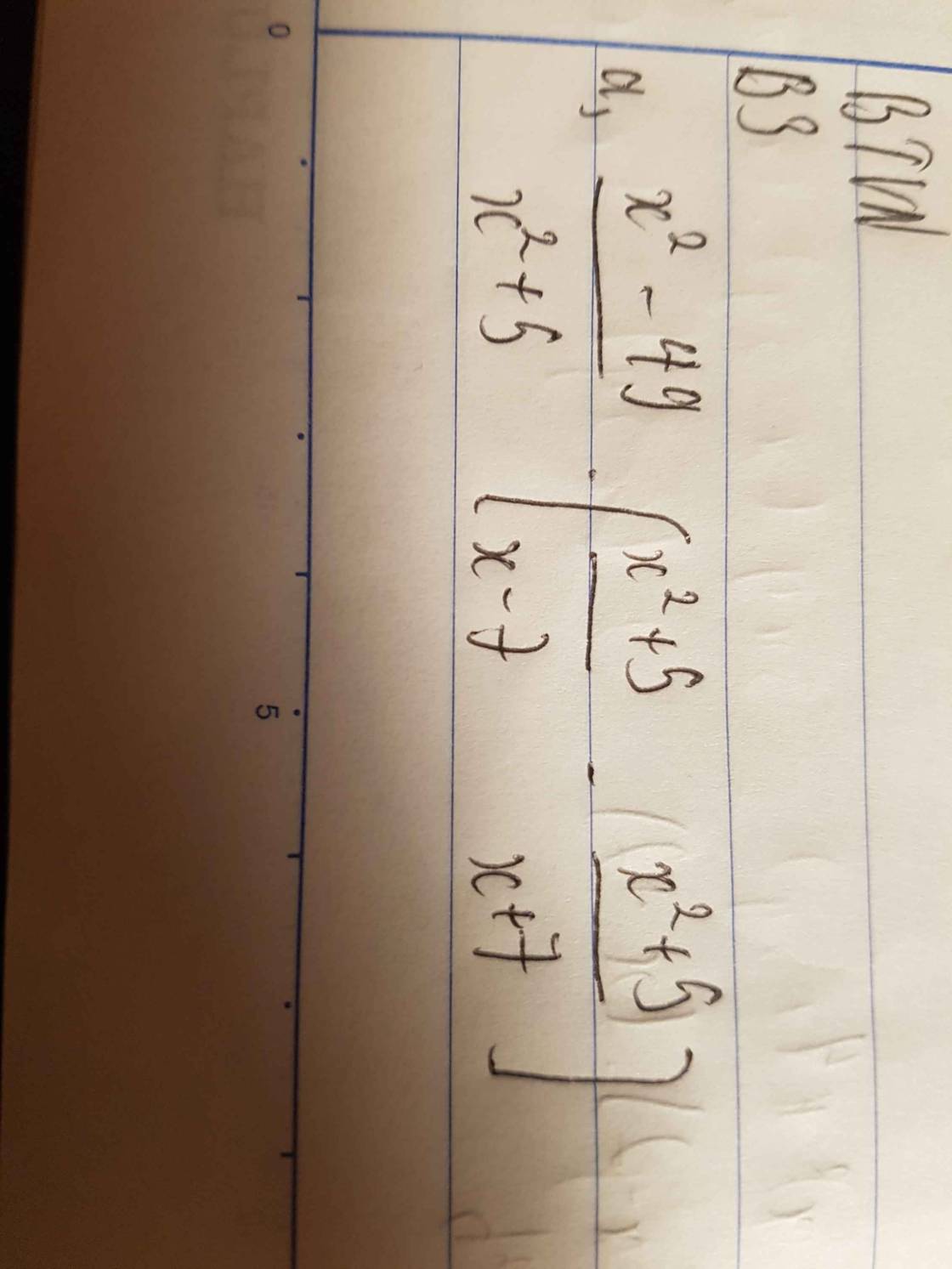
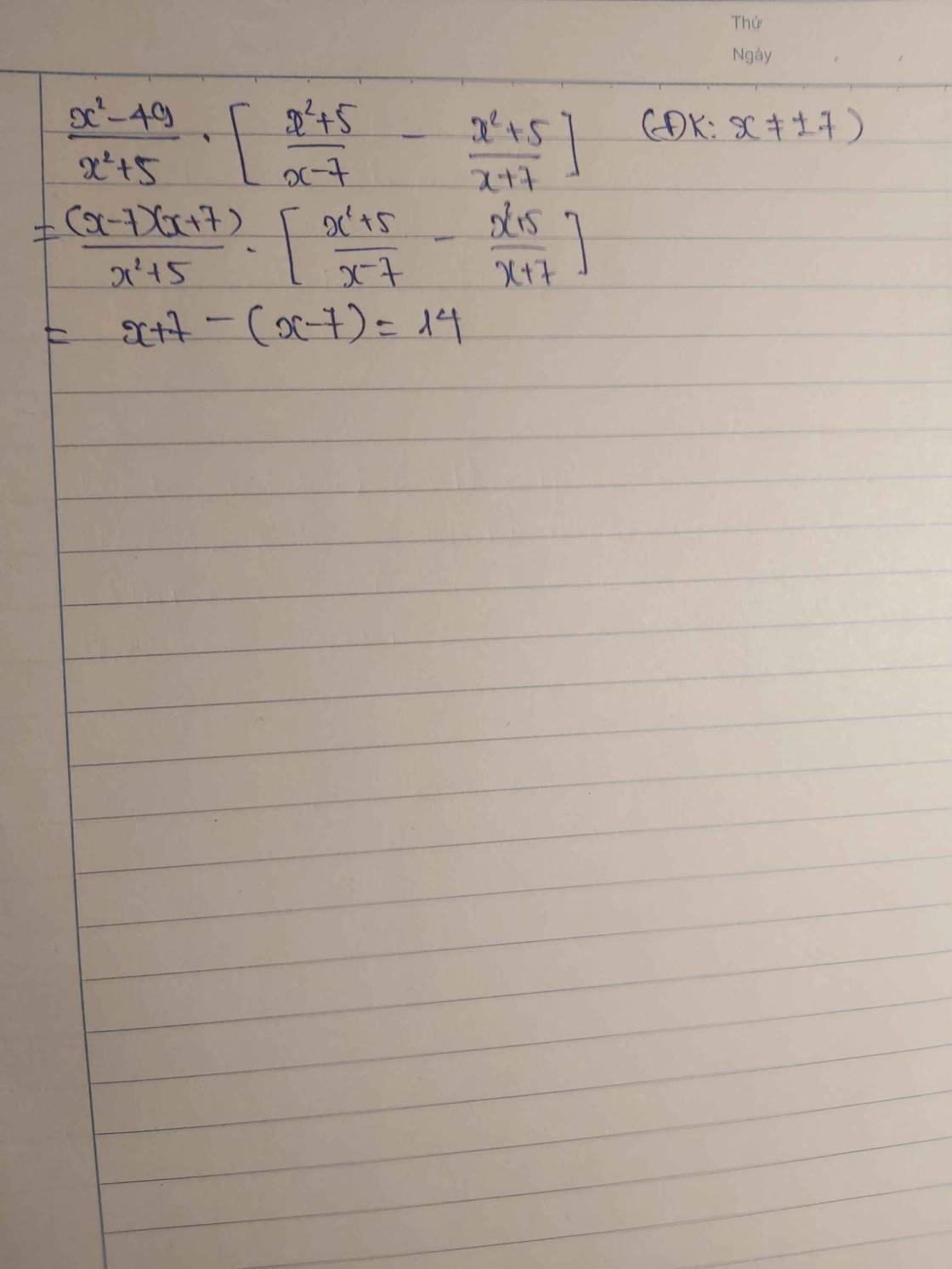
\(B=3x^2+3y^2+z^2+5xy-3yz-3xz-2x-2y+3\)
\(2B=2\cdot\left(3x^2+3y^2+z^2+5xy-3yz-3xz-2x-2y+3\right)\)
\(2B=6x^2+6y^2+2z^2+10xy-6yz-6xz-4x-4y+6\)
\(2B=\left(x^2-2xy+y^2\right)+\left(x^2+2xy+y^2-4x-4y+4\right)+\left(4x^2+4y^2+2z^2+10xy-6yz-6xz+2\right)\)
\(4B=2\left(x-y\right)^2+2\left(x^2+y^2+2^2+2\cdot x\cdot y-2\cdot x\cdot2-2\cdot y\cdot2\right)+2\left(4x^2+4y^2+2z^2+10xy-6yz-6xz+2\right)\)
\(4B=\left(x-y\right)^2+\left(x^2-2xy+y^2\right)+2\left(x+y-2\right)^2+\left(8x^2+8y^2+4z^2+20xy-12yz-12xz+4\right)\)
\(4B=\left(x-y\right)^2+2\left(x+y-2\right)^2+\left(9x^2+9y^2+4z^2+18xy-12yz-12xz+4\right)\)
\(4B=\left(x-y\right)^2+2\left(x+y-2\right)^2+\left[\left(3x\right)^2+\left(3y\right)^2+\left(2z\right)^2+2\cdot3x\cdot3y-2\cdot3x\cdot2z-2\cdot3y\cdot2z\right]+4\)
\(4B=\left(x-y\right)^2+2\left(x+y-2\right)^2+\left(3x+3y-2z\right)^2+4\)
\(B=\dfrac{\left(x-y\right)^2}{4}+\dfrac{\left(x+y-2\right)^2}{2}+\dfrac{\left(3x+3y-2z\right)^2}{4}+1\)
Ta có: \(\left\{{}\begin{matrix}\dfrac{\left(x-y\right)^2}{4}\ge0\forall x,y\\\dfrac{\left(x+y-2\right)^2}{2}\ge0\forall x,y\\\dfrac{\left(3x+3y-2z\right)^2}{4}\ge0\forall x,y,z\end{matrix}\right.\)
\(\Rightarrow B=\dfrac{\left(x-y\right)^2}{4}+\dfrac{\left(x+y-2\right)^2}{2}+\dfrac{\left(3x+3y-2z\right)^2}{4}+1\ge1\forall x,y,z\)
Dấu "=" xảy ra: \(\left\{{}\begin{matrix}x-y=0\\x+y-2=0\\3x+3y-2z=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y\\2x-2=0\\3x+3x-2z=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=y=1\\z=3\end{matrix}\right.\)
Vậy: ...