Cho tam giác abc vuông tại A ( AB < AC). BH là phân giác của góc ABC( H thuộc AC). Lấy D là hình chiếu của H trên BC. a. Tam giác ABH = Tam giác DBH b. BH là đường trung trực của AD c. Kẻ CK vuông góc BH (K thuộc BH). chứng minh tam giác AHK cân d. Ba đường thẳng AB, CK, DH cũng đi qua 1 điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: R(x)-S(x)
\(=2x^3+x^2+x+2-x^3-x^2+x-2\)
\(=x^3+2x\)
R(x)+S(x)
\(=2x^3+x^2+x+2+x^3+x^2-x+2\)
\(=3x^3+2x^2+4\)
b: Đặt R(x)-S(x)=0
=>\(x^3+2x=0\)
=>\(x\left(x^2+2\right)=0\)
mà \(x^2+2>=2>0\forall x\)
nên x=0

a: Xét ΔNMA vuông tại M và ΔNBA vuông tại B có
NA chung
\(\widehat{MNA}=\widehat{BNA}\)
Do đó: ΔNMA=ΔNBA
b: ΔNMA=ΔNBA
=>NM=NB
c: Ta có: ΔNMA=ΔNBA
=>AM=AB
=>A nằm trên đường trung trực của MB(1)
Ta có: NM=NB
=>N nằm trên đường trung trực của MB(2)
Từ (1),(2) suy ra NA là đường trung trực của MB
d: Xét ΔNCK có
CB,KM là các đường cao
CB cắt KM tại A
Do đó: A là trực tâm của ΔNCK
=>NA\(\perp\)CK

Câu 3:
1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔADB=ΔAEC
=>\(AD=AE\)
2: Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
mà HK\(\perp\)BC
nên A,H,K thẳng hàg
=>AK\(\perp\)BC tại K
ΔABC cân tại A
mà AK là đường cao
nên AK là phân giác của góc BAC
Câu 4:
\(f\left(-1\right)\cdot f\left(2\right)\)
\(=\left(-a+b-c+d\right)\cdot\left(8a+4b+2c+d\right)\)
\(=\left(-a+b+c-2c+d\right)\left(8a+4b+4c-2c+d\right)\)
\(=\left(-a-3a-2c+d\right)\left(8a+4\cdot\left(-3a\right)-2c+d\right)\)
\(=\left(-4a-2c+d\right)\left(-4a-2c+d\right)=\left(-4a-2c+d\right)^2\) là bình phương của một số nguyên

x=2022 nên x+1=2023
\(M\left(x\right)=x^{2023}-2023\left(x^{2022}-x^{2021}+x^{2020}-...+x^2-x\right)\)
\(=x^{2023}-\left(x+1\right)\left(x^{2022}-x^{2021}+...+x^2-x\right)\)
\(=x^{2023}-x^{2023}-x^{2022}+x^{2022}+x^{2021}+...-x^3-x^2+x^2+x\)
=x
=2022

a: Sửa đề: ΔAKB và ΔAKC
Xét ΔAKB và ΔAKC có
AK chung
\(\widehat{KAB}=\widehat{KAC}\)
AB=AC
Do đó: ΔAKB=ΔAKC
b: ΔAKB=ΔAKC
=>KB=KC
=>ΔKBC cân tại K
c: Ta có: ΔABC cân tại A
mà AD là đường phân giác
nên AD\(\perp\)BC

\(x^2\left(x+y\right)-y^2\left(x+y\right)+2\left(x^2+y^2\right)+2\left(x+y\right)\)
\(=-2x^2+2y^2+2x^2+2y^2+2\left(x+y\right)\)
\(=4y^2+2\cdot\left(-2\right)=4y^2-4\)

\(M=4x^4+7x^2y^2+3y^4+5y^2\)
\(=4x^4+4x^2y^2+3x^2y^2+3y^4+5y^2\)
\(=4x^2\left(x^2+y^2\right)+3y^2\left(x^2+y^2\right)+5y^2\)
\(=4x^2\cdot5+3y^2\cdot5+5y^2\)
\(=20x^2+20y^2=20\cdot5=100\)
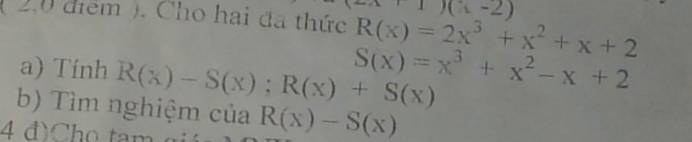



a: Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
\(\widehat{ABH}=\widehat{DBH}\)
Do đó: ΔBAH=ΔBDH
b: ΔBAH=ΔBDH
=>BA=BD và HA=HD
ta có:BA=BD
=>B nằm trên đường trung trực của AD(1)
ta có: HA=HD
=>H nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra BH là đường trung trực của AD
d: Gọi M là giao điểm của CK với BA
Xét ΔBMC có
BK,CA là các đường cao
BK cắt CA tại H
Do đó: H là trực tâm của ΔBMC
=>MH\(\perp\)BC
mà HD\(\perp\)BC
nên M,H,D thẳng hàng
=>BA,DH,CK đồng quy