cho tam giác ABC vuông tại A có AB=3cm; BC=5cm; AC=4cm.
a) So sánh các góc của tam giác ABC.
b) Trên tia đối của tia AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD.Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AC tại M. tính MC.
c) Đường trung trực d của đoạn thẳng AC cắt đường thẳng DC tại Q. chứng minh ba điểm B, M, Q thẳng hàng.
giải nhanh giúp mik vs nha mik đag cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta thấy: $(x+1)^{2022}\geq 0$ với mọi $x$
$\Rightarrow A=(x+1)^{2022}+2023\geq 0+2023=2023$
Vậy $A_{\min}=2023$
Giá trị này đạt được tại $x+1=0\Leftrightarrow x=-1$

\(P\left(x\right)⋮x-2\)
=>\(x^4-3x^3+5x^2+ax-a⋮x-2\)
=>\(x^4-2x^3-x^3+2x^2+3x^2-6x+\left(a+6\right)x-\left(2a+12\right)+2a+12-a⋮x-2\)
=>a+12=0
=>a=-12

\(P=\left|2018-x\right|+\left|2019-x\right|\)
\(=\left|x-2018\right|+\left|2019-x\right|>=\left|x-2018+2019-x\right|=1\)
Dấu '=' xảy ra khi 2018<=x<=2019

\(4x^2-5x+a⋮2x-3\)
=>\(4x^2-6x+x-1,5+a+1,5⋮2x-3\)
=>a+1,5=0
=>a=-1,5

Đặt D(x)=0
=>\(x^2-7x+10=0\)
=>\(x^2-2x-5x+10=0\)
=>x(x-2)-5(x-2)=0
=>(x-2)(x-5)=0
=>\(\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

a: \(P\left(x\right)=2x^2-2x^4-4x-1+x^3\)
\(=-2x^4+x^3+2x^2-4x-1\)
\(Q\left(x\right)=x^3-4x-4-3x^4\)
\(=-3x^4+x^3-4x-4\)
b: \(P\left(x\right)=-2x^4+x^3+2x^2-4x-1\)
=>Bậc là 4
\(Q\left(x\right)=-3x^4+x^3-4x-4\)
=>Bậc là 4
c: P(x)+Q(x)
\(=-2x^4+x^3+2x^2-4x-1-3x^4+x^3-4x-4\)
\(=-5x^4+2x^3+2x^2-8x-5\)

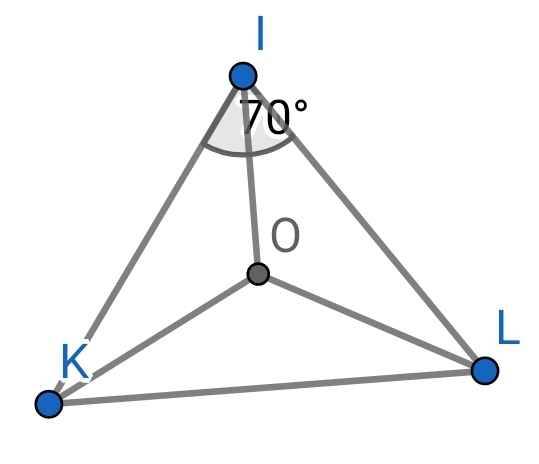
a) Do KO là tia phân giác của ∠IKL (gt)
⇒ ∠OKL = ∠OKI = ∠IKL : 2
Do LO là tia phân giác của ∠ILK (gt)
⇒ ∠ILO = ∠OLK = ∠ILK : 2
∆IKL có:
∠IKL + ∠ILK + ∠KIL = 180⁰ (tổng ba góc trong ∆IKL)
⇒ ∠IKL + ∠ILK = 180⁰ - ∠KIL
= 180⁰ - 70⁰
= 110⁰
⇒ ∠OKL + ∠OLK = ∠IKL : 2 + ∠ILK : 2
= (∠IKL + ∠ILK) : 2
= 110⁰ : 2
= 55⁰
∆OKL có:
∠OKL + ∠OLK + ∠KOL = 180⁰ (tổng ba góc trong ∆OKL)
⇒ ∠KOL = 180⁰ - (∠OKL + ∠OLK)
= 180⁰ - 55⁰
= 125⁰
b) Do KO và LO là hai đường phân giác của ∆KIL (gt)
⇒ IO là đường phân giác thứ ba của ∆KIL
⇒ IO là tia phân giác của ∠KIL
⇒ ∠KIO = ∠KIL : 2
= 70⁰ : 2
= 35⁰
c) Do O là giao điểm của ba đường phân giác của ∆KIL
⇒ O cách đều ba cạnh của ∆KIL

Chiều rộng hình chữ nhật là:
\(18:2=9\left(m\right)\)
Chiều dài hình chữ nhật:
\(9+3=12\left(m\right)\)
Ta gọi a là chiều rộng.
Ta có:
(a + 3) x a = S
(a + 3 + 2) x a = S + 18
(a + 5) x a = S + 18
(a + 5) x a - (a + 3) x a = S + 18 - S
2a = 18
a = 18 : 2
a = 9
⇒ Chiều rộng của hình chữ nhật là: 9 cm
⇒ Chiều dài của hình chữ nhật là: 9 + 3 = 12 (cm)
Đáp số: Chiều rộng: 9 cm
Chiều dài: 12 cm
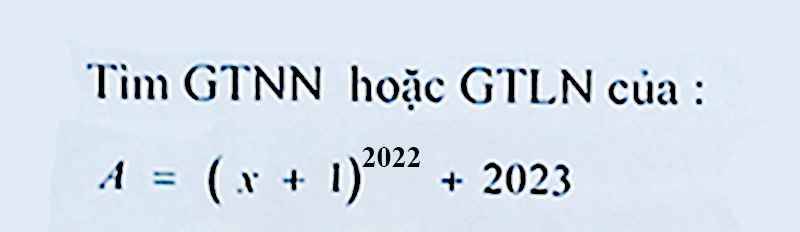

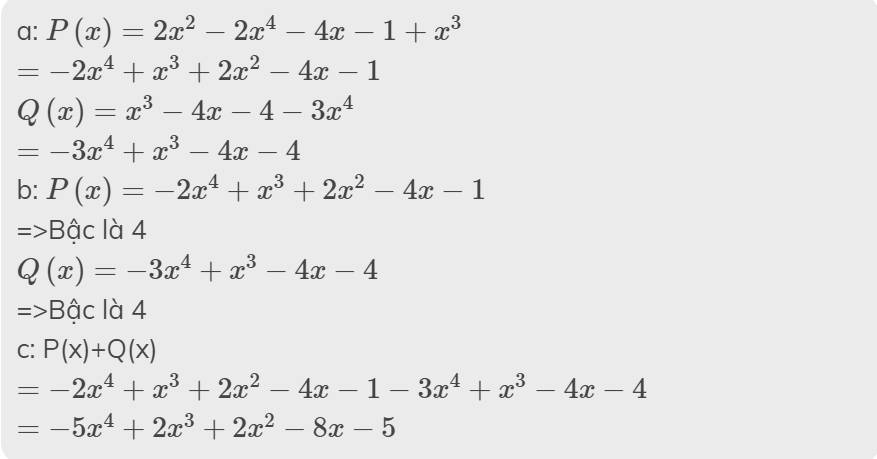
a: Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Xét ΔCDB có
CA,DK là các đường trung tuyến
CA cắt DK tại M
Do đó: M là trọng tâm của ΔCDB
=>\(CM=\dfrac{2}{3}CA=\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(cm\right)\)
c: Gọi I là trung điểm của AC
d là trung trực của AC
mà I là trung điểm của AC
nên IQ\(\perp\)AC tại I
=>IQ//AD
Xét ΔCAD có
I là trung điểm của AC
IQ//AD
Do đó: Q là trung điểm của CD
Xét ΔCDB có
M là trọng tâm
Q là trung điểm của CD
Do đó: B,M,Q thẳng hàng