a

ta có: MN\(\perp\)AC

AB\(\perp\)AC

Do đó: MN//AB

ta có: MP\(\perp\)AB

AC\(\perp\)AB

Do đó: MP//AC

Xét ΔBMP vuông tại P và ΔMCN vuông tại N có

\(\widehat{MBP}=\widehat{CMN}\)(hai góc đồng vị, MN//AB)

Do đó: ΔBMP~ΔMCN

b: Xét ΔBAC có MP//AC

nên \(\dfrac{MP}{AC}=\dfrac{BM}{BC}\)

=>\(\dfrac{MP}{12}=\dfrac{6}{15}=\dfrac{2}{5}\)

=>\(MP=12\cdot\dfrac{2}{5}=4,8\left(cm\right)\)

Xét ΔCAB có MN//AB

nên \(\dfrac{MN}{AB}=\dfrac{CM}{CB}\)

=>\(\dfrac{MN}{9}=\dfrac{9}{15}=\dfrac{3}{5}\)

=>MN=9*3/5=5,4(cm)

Xét tứ giác APMN có \(\widehat{APM}=\widehat{ANM}=\widehat{PAN}=90^0\)

nên APMN là hình chữ nhật

=>\(AM^2=MN^2+MP^2=5,4^2+4,8^2=52,2\)

=>\(AM=\sqrt{52,2}\left(cm\right)\)

a) \(4x^2-1=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x\right)^2-1^2=\left(2x+1\right)\left(3x-5\right)\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1\right)-\left(2x+1\right)\left(3x-5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(2x-1-3x+5\right)=0\)

\(\Leftrightarrow\left(2x+1\right)\left(4-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-1\\4=x\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=4\end{matrix}\right.\)

Vậy: ...

b) \(\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}=10\)

\(\Leftrightarrow\dfrac{x-85}{15}+\dfrac{x-74}{13}+\dfrac{x-67}{11}+\dfrac{x-64}{9}-10=0\)

\(\Leftrightarrow\left(\dfrac{x-85}{15}-1\right)+\left(\dfrac{x-74}{13}-2\right)+\left(\dfrac{x-67}{11}-3\right)+\left(\dfrac{x-64}{9}-4\right)=0\)

\(\Leftrightarrow\dfrac{x-100}{15}+\dfrac{x-100}{13}+\dfrac{x-100}{11}+\dfrac{x-100}{9}=0\)

\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{15}+\dfrac{1}{13}+\dfrac{1}{11}+\dfrac{1}{9}\right)=0\)

\(\Leftrightarrow x-100=0\)

\(\Leftrightarrow x=100\)

Vậy: ... 

a) Bảng giá trị

  Đồ thị:

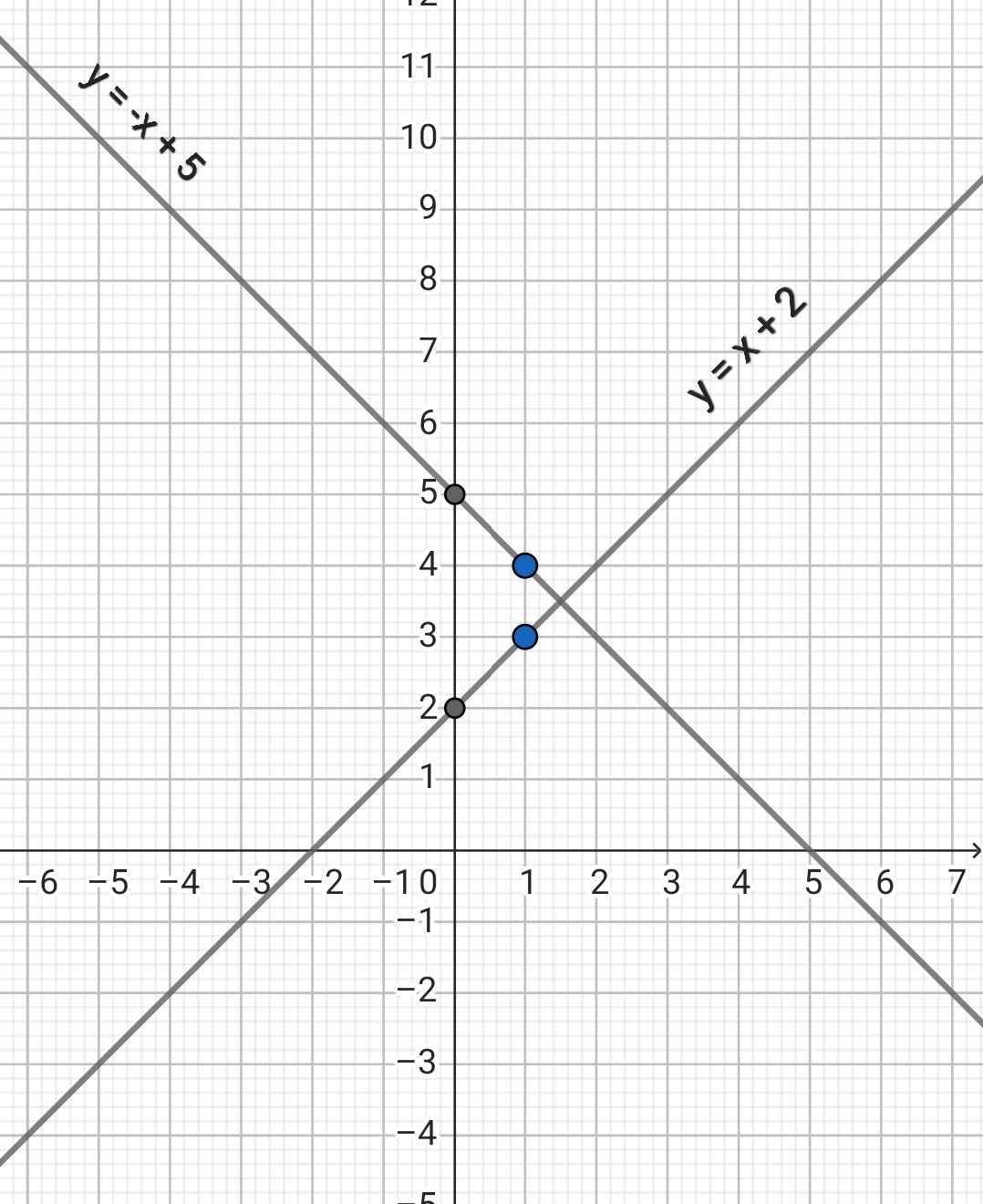
b) Phương trình hoành độ giao điểm của (d₁) và (d₂):

-x + 5 = x + 2

-x - x = 2 - 5

-2x = -3

x = 3/2

Thay x = 3/2 vào (d₂), ta có:

y = 3/2 + 2 = 7/2

Vậy tọa độ giao điểm M(3/2; 7/2)

c) Gọi (d₃): y = ax + b (a ≠ 0) là đồ thị của hàm số cần tìm

Do (d₃) // (d₁) nên a = -1

⇒ (d₃): y = -x + b

Do (d₃) đi qua K(-4; 2) nên thay tọa độ của K(-4; 2) vào (d₃), ta có:

-(-4) + b = 2

b = 2 - 4

b = -2

Vậy hàm số cần tìm là:

y = -x - 2

a) Đồ thị hs:`y=-2x+5` cắt `Ox(5/2;0)` và cắt `Oy(0;5)` 

Đồ thị hs: `y=x+2` cắt `Ox(-2;0)` và cắt `Oy(0;2)` 

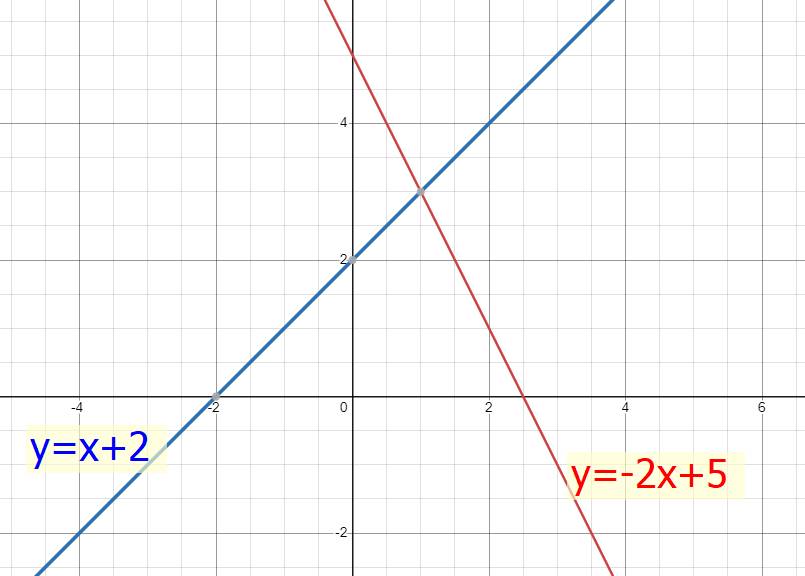
b) Ta có pt hoành độ giao điểm của (d₁) và (d₂): 

\(-2x+5=x+2\)

\(\Leftrightarrow x+2x=5-2\)

\(\Leftrightarrow3x=3\)

\(\Leftrightarrow x=1\)

Thay `x=1` vào `(d_2)` ta có: \(y=1+2=3\)

`=>M(1;3)` 

c) Hàm số `y=ax+b` có đồ thị song song với `(d_1):y=-2x+5` 

`=>a=-2` 

`=>y=-2x+b` 

Mà hàm số này đi qua điểm `K(-4;2)` ta thay `x=-4` và `y=2` vào ta có:

`2=-2*(-4)+b`

`<=>2=8+b`

`<=>b=2-8=-6` 

Vậy hàm số đó là: `y=-2x-6` 

ĐKXĐ: x ≠ 1; x ≠ -1

4/(x - 1) - A = 8/(x² - 1)

⇒ A = 4/(x - 1) - 8/(x² - 1)

= 4(x + 1)/(x² - 1) - 8/(x² - 1)

= (4x + 4 - 8)/(x² - 1)

= (4x - 4)/(x² - 1)

= 4(x - 1)/[(x - 1)(x + 1)]

= 4/(x + 1)

mình đang cần gấp

a: Xét ΔAFB và ΔCFI có

\(\widehat{FAB}=\widehat{FCI}\)(hai góc so le trong, AB//CI)

\(\widehat{AFB}=\widehat{CFI}\)(hai góc đối đỉnh)

Do đó: ΔAFB~ΔCFI

b: Xét ΔEAB và ΔEKD có

\(\widehat{EAB}=\widehat{EKD}\)(hai góc so le trong, AB//KD)

\(\widehat{AEB}=\widehat{KED}\)(hai góc đối đỉnh)

Do đó: ΔEAB~ΔEKD

=>\(\dfrac{AB}{KD}=\dfrac{AE}{KE}\)

=>\(AB\cdot KE=AE\cdot KD\)

\(6x^2+4xy-y^2\)

\(=6\left(x^2+\dfrac{2}{3}xy-\dfrac{1}{6}y^2\right)\)

\(=6\left(x^2+2\cdot x\cdot\dfrac{1}{3}y+\dfrac{1}{9}y^2-\dfrac{5}{18}y^2\right)\)

\(=6\left[\left(x+\dfrac{1}{3}y\right)^2-\left(\dfrac{y\sqrt{5}}{3\sqrt{2}}\right)^2\right]\)

\(=6\left(x+\dfrac{1}{3}y-\dfrac{y\sqrt{10}}{6}\right)\left(x+\dfrac{1}{3}y+\dfrac{y\sqrt{10}}{6}\right)\)

b: \(8x^2+3xy-4y^2\)

\(=8\left(x^2+\dfrac{3}{8}xy-\dfrac{1}{2}y^2\right)\)

\(=8\left(x^2+2\cdot x\cdot\dfrac{3}{16}y+\dfrac{9}{256}y^2-\dfrac{137}{256}y^2\right)\)

\(=8\left[\left(x+\dfrac{3}{16}y\right)^2-\left(\dfrac{y\sqrt{137}}{16}\right)^2\right]\)

\(=8\left(x+\dfrac{3}{16}y-\dfrac{y\sqrt{137}}{16}\right)\left(x+\dfrac{3}{16}y+\dfrac{y\sqrt{137}}{16}\right)\)

1.

\(B=\left(ab+bc+ca\right)\left(\dfrac{ab+bc+ca}{abc}\right)-abc\left(\dfrac{a^2b^2+b^2c^2+c^2a^2}{a^2b^2c^2}\right)\)

\(=\dfrac{\left(ab+bc+ca\right)^2}{abc}-\dfrac{a^2b^2+b^2c^2+c^2a^2}{abc}\)

\(=\dfrac{a^2b^2+c^2c^2+c^2a^2+2abc\left(a+b+c\right)}{abc}-\dfrac{a^2b^2+b^2c^2+c^2a^2}{abc}\)

\(=\dfrac{2abc\left(a+b+c\right)}{abc}=2\left(a+b+c\right)\)

2.

\(x+y+z=xyz\Rightarrow\dfrac{x+y+z}{xyz}=1\)

\(\Rightarrow\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{zx}=1\)

Lại có:

\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=3\Rightarrow\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2=9\)

\(\Rightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}=9\)

\(\Rightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+2.1=9\)

\(\Rightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}=7\)

\(pt:25\left(x+1\right)^4-26\left(x+1\right)^2+1=0\\ \Leftrightarrow\left[25\left(x+1\right)^4-25\left(x+1\right)^2\right]-\left[\left(x+1\right)^2-1\right]=0\\ \Leftrightarrow25\left(x+1\right)^2\left[\left(x+1\right)^2-1\right]-\left[\left(x+1\right)^2-1\right]=0\\ \Leftrightarrow\left[\left(x+1\right)^2-1\right]\left[25\left(x+1\right)^2-1\right]=0\\ \Rightarrow\left[{}\begin{matrix}\left(x+1\right)^2-1=0\\25\left(x+1\right)^2-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=1\\\left(x+1\right)^2=\dfrac{1}{25}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=1\\x+1=-1\\x+1=\dfrac{1}{5}\\x+1=-\dfrac{1}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\\x=-\dfrac{4}{5}\\x=-\dfrac{6}{5}\end{matrix}\right.\)

Vậy tập nghiệm pt: \(S=\left\{0;-2;-\dfrac{4}{5};-\dfrac{6}{5}\right\}\)

\(25\left(x+1\right)^4-26\left(x+1\right)^2+1=0\)

=>\(25\left(x+1\right)^4-25\left(x+1\right)^2-\left(x+1\right)^2+1=0\)

=>\(25\left(x+1\right)^2\left[\left(x+1\right)^2-1\right]-\left[\left(x+1\right)^2-1\right]=0\)

=>\(\left[\left(x+1\right)^2-1\right]\left[25\left(x+1\right)^2-1\right]=0\)

=>\(\left(x+1+1\right)\left(x+1-1\right)\left(5x+5-1\right)\left(5x+5+1\right)=0\)

=>\(x\left(x+2\right)\left(5x+4\right)\left(5x+6\right)=0\)

=>\(\left[{}\begin{matrix}x=0\\x=-2\\x=-\dfrac{4}{5}\\x=-\dfrac{6}{5}\end{matrix}\right.\)