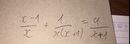\(ĐKXĐ:x\ne\left\{0;-1\right\}\)

\(\frac{x-1}{x}+\frac{1}{x\left(x+1\right)}=\frac{4}{x+1}\)

\(\Leftrightarrow\frac{x^2-1}{x\left(x+1\right)}+\frac{1}{x\left(x+1\right)}-\frac{4x}{x\left(x+1\right)}=0\)

\(\Leftrightarrow x^2-1+1-4x=0\)

\(\Leftrightarrow x^2-4x=0\)

\(\Leftrightarrow x\left(x-4\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\left(ktm\right)\\x=4\left(tm\right)\end{cases}}}\)

Vậy phương trình có nghiệm x = 4

\(\frac{x-1}{x}+\frac{1}{x\left(x+1\right)}=\frac{4}{x+1}\)ĐK : \(x\ne-1;0\)

\(\Leftrightarrow\frac{x^2-1+1}{x\left(x+1\right)}=\frac{4x}{x\left(x+1\right)}\Leftrightarrow x^2-4x=0\Leftrightarrow x=0;x=4\)

Vậy tập nghiệm của pt là S = { 0 ; 4 } 

a, Do \(x=-3\)\(=>A=\frac{x+3}{x+2}=\frac{-3+3}{-3+2}=\frac{0}{-1}=0\)

Vậy A = 0 khi x = -3

b, Ta có : \(B=\frac{x}{x+1}+\frac{2}{x-1}-\frac{4}{x^2-1}=\frac{x\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{2\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}-\frac{4}{x^2-1}\)

\(=\frac{x^2-x+2x-2}{x^2-1}=\frac{x\left(x-1\right)+2\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\frac{\left(x+2\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}\)

\(=\frac{x+2}{x+1}\)(đpcm)

iophkhghoghkghjggjhghgjhjnnrjhnjvfdjgjhrthgfjhnvfgughfuihgjfdhntfjhb fdghxdfjthfgdrtfghertgfhgrthgrthgrtrgurgfhgfhgerhgdsuhtyhdfuyhrhgthfutrugerhtgtertmgiurjhtjyiujbgf89yhjrintjihjdhr hbfbv nùgvuibherufdhtguihruvhaweufhvnfgffyhrghsr78ryughg9u8ghtityjyhyijtyjuy8hituhzihuyuyru9jr0ujtyututr09yuitutr9uirt9ui56i789i69utihirrgiu6ygjityojhojkyjyykikgjkthogfjkjhfggfjkhjkhkjkjkjkjgfohfkojhiyy0jhiuihmokhmhjkhkjykkhjkhjykjkgjkyjyotuhjnhknkhijiyjiyitihfgujdhufturgjjhi htfhrhfgrhuygrutrtuyhrthuyhrhtuhutryjuy.ôl

\(F=a^3+b^3+ab\left(a+b\right)+2a+b+\frac{3}{a}+\frac{2}{b}\)

\(F=\left(a+b\right)^3-3ab\left(a+b\right)+ab\left(a+b\right)+a+b+a+\frac{1}{a}+\frac{2}{a}+\frac{2}{b}\)

\(F=8-4ab+2+a+\frac{1}{a}+\frac{2}{a}+\frac{2}{b}\)

Ta có: \(\left(a+b\right)^2\ge4ab\Leftrightarrow-4ab\ge-\left(a+b\right)^2=-4\)

\(a+\frac{1}{a}\ge2\sqrt{a.\frac{1}{a}}=2\)

\(\frac{2}{a}+\frac{2}{b}\ge\frac{8}{a+b}=4\)

Suy ra \(F\ge8-4+2+2+4=12\)

Dấu \(=\)xảy ra khi \(a=b=1\).

(x-5)²=36

<=>\(\orbr{\begin{cases}x-5=6\\x-5=-6\end{cases}}\)<=> \(\orbr{\begin{cases}x=11\\x=-1\end{cases}}\)

Vậy:...

\(\left(x-5\right)^2-36=0\)

\(\left(x-5\right)^2=0+36\)

\(\left(x-5\right)^2=36\)

\(\left(x-5\right)^2=\pm6^2\)

\(\Rightarrow x-5=6\text{ hoặc }x-5=-6\)

     \(x=6+5\)        \(x=-6+5\)

     \(x=11\)              \(x=-1\)

Vậy x = 11; x = -1