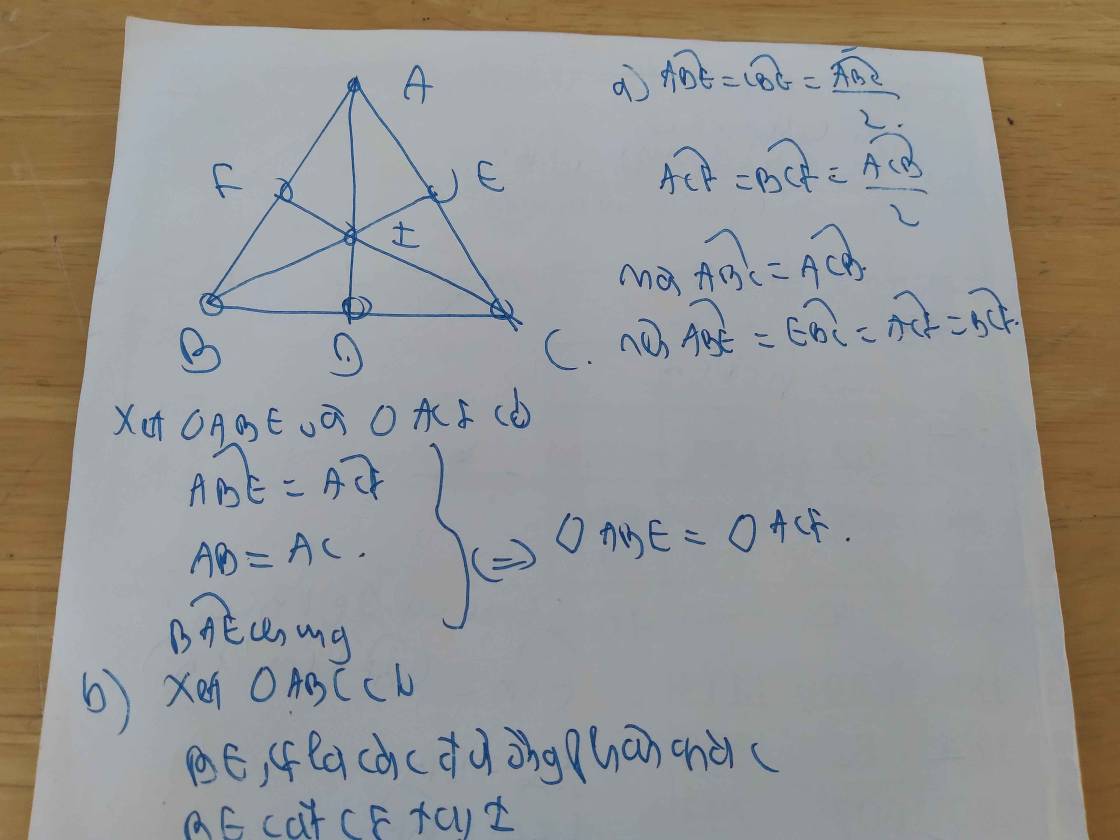
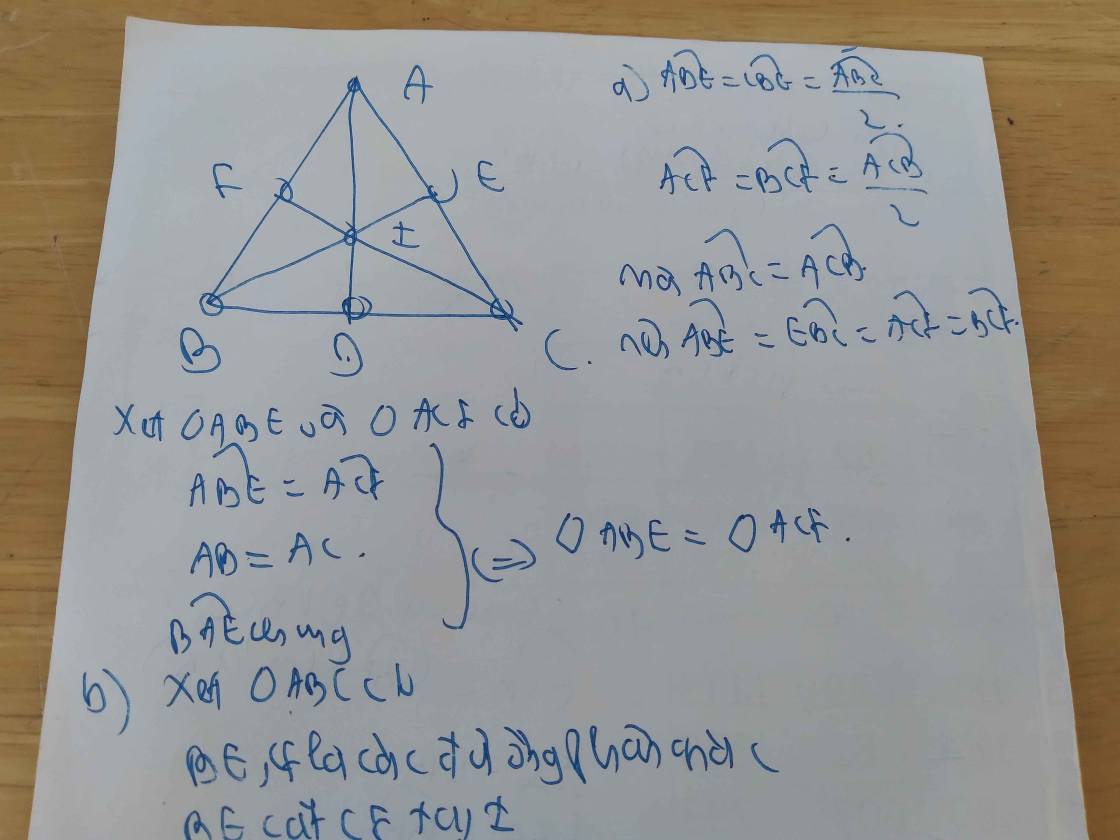
Cho tam giác ABC cân ở A. Các đường phân giác BE, CF cắt nhau tại điểm I.
a) Chứng minh tam giác ABE = tam giác ACF.
b) Tía AI cắt BC tại điểm D. Chứng minh D là trung điểm của đoạn thẳng BC và EF vuông góc với AD.
e) Cho IC = 2ID. Chứng minh tam giác ABC là tam giác đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Lời giải:
b.
$(x-1)(x+2)-(x+1)(x-3)-3x=1$
$\Leftrightarrow (x^2+x-2)-(x^2-2x-3)-3x=1$
$\Leftrightarrow x^2+x-2-x^2+2x+3-3x=1$
$\Leftrightarrow 0=0$ (luôn đúng)
Vậy PT có nghiệm $x$ là số thực bất kỳ
c.
$(3x+7)(2x+3)-(3x-5)(2x+11)=0$
$\Leftrightarrow (6x^2+23x+21)-(6x^2+23x-55)=0$
$\Leftrightarrow 76=0$ (vô lý)
Vậy không tồn tại $x$ thỏa mãn đề.

Lời giải:
$x^3-(x-2)(x^2+x-1)=4(x^2-2)$
$\Leftrightarrow x^3-(x^3+x^2-x-2x^2-2x+2)=4x^2-8$
$\Leftrightarrow x^3-(x^3-x^2-3x+2)=4x^2-8$
$\Leftrightarrow x^3-x^3+x^2+3x-2=4x^2-8$
$\Leftrightarrow x^2+3x-2=4x^2-8$
$\Leftrightarrow 3x^2-3x-6=0$
$\Leftrightarrow x^2-x-2=0$
$\Leftrightarrow (x+1)(x-2)=0$
$\Rightarrow x+1=0$ hoặc $x-2=0$
$\Rightarrow x=-1$ hoặc $x=2$

Lời giải:
1.
$A=3(x-3)+5-2(x-1)=3x-9+5-2x+2=(3x-2x)+(-9+5+2)=x-2=0$
$\Rightarrow x=2$
Vậy $x=2$ là nghiệm của đa thức.
2.
$B=x^2(3x+2)-2x(x-2)=3x^3+2x^2-2x^2+4x=3x^3+4x=x(3x^2+4)=0$
$\Rightarrow x=0$ hoặc $3x^2+4=0$
Nếu $3x^2+4=0$
$\Rightarrow 3x^2=-4<0$ (vô lý)
$\Rightarrow x=0$
Vậy $x=0$ là nghiệm của $B$
3.
$C=x^3+3x(x-2)-x(3x-7)=x^3+3x^2-6x-3x^2+7x=x^3+x=x(x^2+1)=0$
$\Rightarrow x=0$ hoặc $x^2+1=0$
Nếu $x^2+1=0$
$\Rightarrow x^2=-1<0$ (vô lý)
$\Rightarrow x=0$
Vậy $x=0$ là nghiệm duy nhất của $C$.

Lời giải:
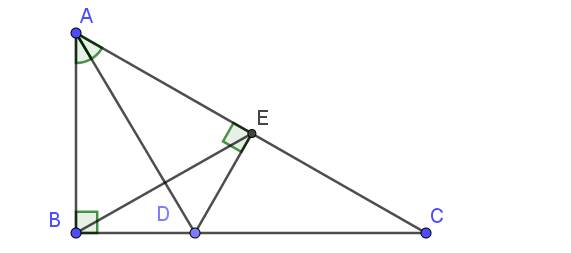
a.
Tam giác $ABC$ vuông tại $B$ nên $\widehat{ABC}=90^0$
Xét tam giác $ABC$ có:
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0$ (tổng 3 góc trong 1 tam giác)
$\Rightarrow 90^0+30^0+\widehat{BAC}=180^0$
$\Rightarrow \widehat{BAC}=60^0$
b.
Xét tam giác $BAD$ và $EAD$ có:
$AD$ chung
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là phân giác $\widehat{A}$)
$\widehat{ABD}=\widehat{AED}=90^0$
$\Rightarrow \triangle BAD=\triangle EAD$ (ch-gn)
c.
Từ tam giác bằng nhau phần b suy ra $AB=AE$
$\Rightarrow ABE$ cân tại $A$
$\Rightarrow \widehat{ABE}=\widehat{AEB}$
Mà $\widehat{BAE}=60^0$ (kết quả phần a) nên:
$\widehat{ABE}=\widehat{AEB}=(180^0-\widehat{BAE}):2=(180^0-60^0):2=60^0$
Vậy $\widehat{ABE}=\widehat{AEB}=\widehat{BAE}=60^0$ nên $ABE$ là tam giác đều.