\(\dfrac{1995}{1997}\times\dfrac{1009}{1993}\times\dfrac{997}{1995}\times\dfrac{1997}{995}\)

\(=\dfrac{1995}{1995}\times\dfrac{1997}{1997}\times\dfrac{997}{995}\times\dfrac{1009}{1993}=\dfrac{1009\times997}{995\times1993}\)

\(=\dfrac{1005973}{1983035}\)

Đề không đủ dữ kiện để tính toán. Bạn xem lại.

-Trung binh moi gio ca no di xuoi dong la:

1:32=1/32(quang duong song AB)

-Trung binh moi gio ca no di nguoc dong la:

1:48=1/48(quang duong song  AB)

-Vi hieu van toc xuoi dong va nguoc dong bang 2 lan van toc dong nuoc , nen moi gio cum beo troi duoc la:

(1/32-1/48):2=1/192(quang duong song AB)

-Thoi gian cum beo tri tu A den B la:

1:1/192=192 phut

Dap so: 192 phut

Lời giải:

$50,87\times y+12,09\times y+37,04\times y=256+144$

$y\times (50,87+12,09+37,04)=400$

$y\times 100=400$

$y=400:100=4$

50,87xY+12,09xY+37,04xY=256+144

50,87xy+12,09xy+37,04xy=400

Yx(50,87+37,04+12,09)=400

Yx100                           = 400 

y=400:100

y=4

số La Mã

đúng rồi nha

\(\dfrac{x+1}{3}=\dfrac{y-2}{4}=\dfrac{z-1}{13}\)

=>\(\dfrac{2x+2}{6}=\dfrac{3y-6}{12}=\dfrac{z-1}{13}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{2x+2}{6}=\dfrac{3y-6}{12}=\dfrac{z-1}{13}=\dfrac{2x-3y+z+2+6-1}{6-12+13}=\dfrac{49}{7}=7\)

=>\(\dfrac{x+1}{3}=\dfrac{y-2}{4}=\dfrac{z-1}{13}=7\)

=>\(x+1=21;y-2=28;z-1=91\)

=>x=20; y=30; z=92

Lời giải:

Áp dụng TCDTSBN:

$\frac{x+1}{3}=\frac{y-2}{4}=\frac{z-1}{13}$

$=\frac{2(x+1)}{6}=\frac{3(y-2)}{12}=\frac{z-1}{13}$

$=\frac{2(x+1)-3(y-2)+(z-1)}{6-12+13}=\frac{2x-3y+z+7}{7}=\frac{42+7}{7}=7$

$\Rightarrow x+1=3.7=21; y-2=4.7=28; z-1=13.7=91$

$\Rightarrow x=20; y=30; z=92$

a: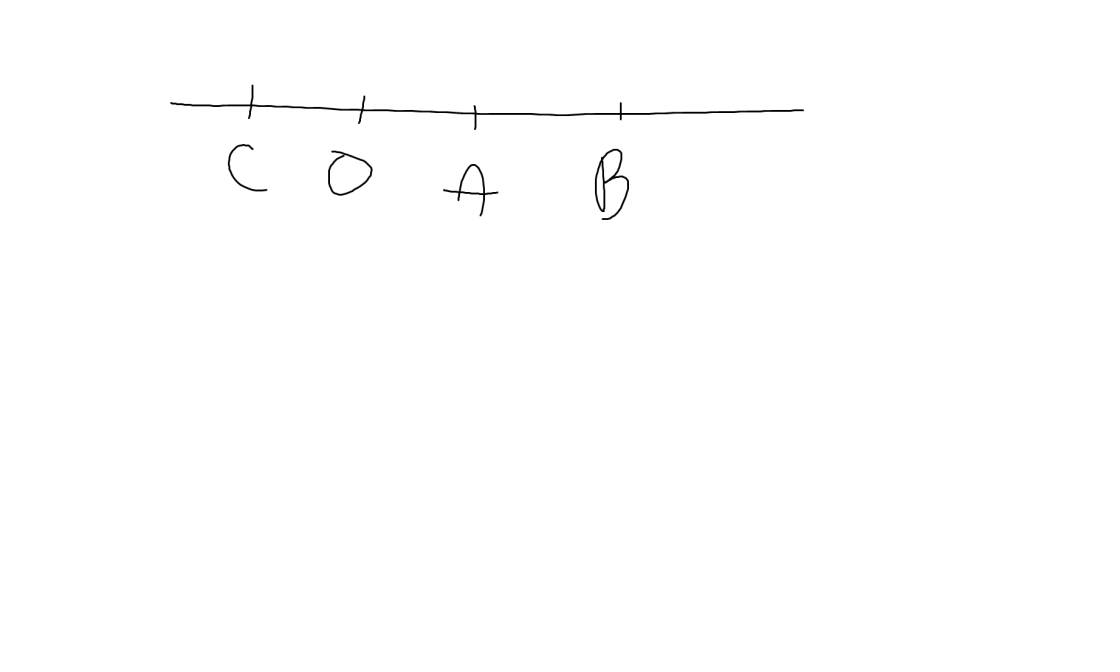 

b: OA=2cm

OB=4cm

mà 2<4

nên OA<OB

c: Sửa đề: OC=2cm

Vì OA và OC là hai tia đối nhau

nên O nằm giữa A và C

Ta có: O nằm giữa A và C

OA=OC(=2cm)

Do đó: O là trung điểm của AC

d: Các đoạn thẳng trên hình vẽ là CO,CA,CB,OA,OB,AB

=>Có 6 đoạn

mik dốt hình lắm nên ko bt lm hình nha bn.

(1,1+1,2+...+1,19)x(12,5x46-25x23)

=(1,1+1,2+...+1,19)x(575-575)

=0

Diện tích 4 bức tường là:

\(\left(6+4\right)\times2\times8=160\left(m^2\right)\)

Diện tích cần quét sơn là:

160-8,16=151,84(m²)

Lời giải:

Diện tích 4 bức tường là:
$2\times 8\times (6+4)=160$ (m²)

Diện tích quét sơn:

$160-8,16=151,84$ (m²)

Diện tích xung quanh bể:

(3 + 1,8) × 2 × 1,6 = 15,36 (m²)

Diện tích đáy bể:

3 × 1,8 = 5,4 (m²)

Diện tích lát gạch:

15,36 + 5,4 = 20,76 (m²) = 2076 (dm²)

Diện tích viên gạch:

2 × 2 = 4 (dm²)

Số viên gạch cần dùng:

2076 : 4 = 519 (viên)

a: \(M\left(x\right)=5-8x^4+2x^3+x+\left(5x^2+1\right)x^2-4x^3\)

\(=5-8x^4+\left(2x^3-4x^3\right)+x+5x^4+x^2\)

\(=-3x^4-2x^3+x^2+x+5\)

\(N\left(x\right)=x\left(3x^4+x^3-4\right)-\left(4x^3-7+2x^4+3x^5\right)\)

\(=3x^5+x^4-4x-4x^3+7-2x^4-3x^5\)

\(=-x^4-4x^3-4x+7\)

b: P(x)=M(x)+N(x)

\(=-3x^4-2x^3+x^2+x+5-x^4-4x^3-4x+7\)

\(=-4x^4-6x^3+x^2-3x+12\)

Q(x)=M(x)-N(x)

\(=-3x^4-2x^3+x^2+x+5+x^4+4x^3+4x-7\)

\(=-2x^4+2x^3+x^2+5x-2\)

c: \(P\left(1\right)=-4\cdot1^4-6\cdot1^3+1^2-3\cdot1+12\)

=-4-6+1-3+12

=-10-2+12

=0

=>x=1 là nghiệm của P(x)

\(Q\left(1\right)=-2\cdot1^4+2\cdot1^3+1^2+5\cdot1-2\)

=-2+2+1+5-2

=4

=>x=1 không là nghiệm của P(x)

d: \(F\left(x\right)=Q\left(x\right)-\left(-2x^4+2x^3+x^2-12\right)\)

\(=-2x^4+2x^3+x^2+5x-2+2x^4-2x^3-x^2+12\)

=5x+10

Đặt F(x)=0

=>5x+10=0

=>5x=-10

=>x=-2