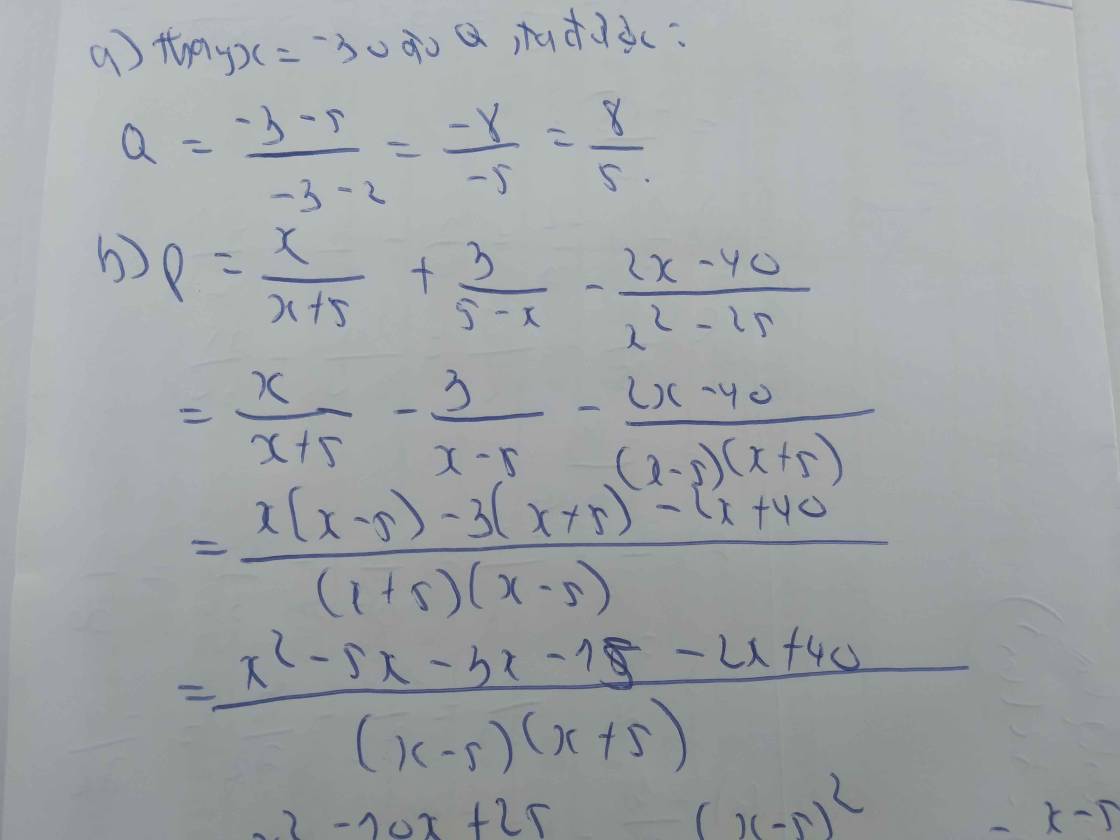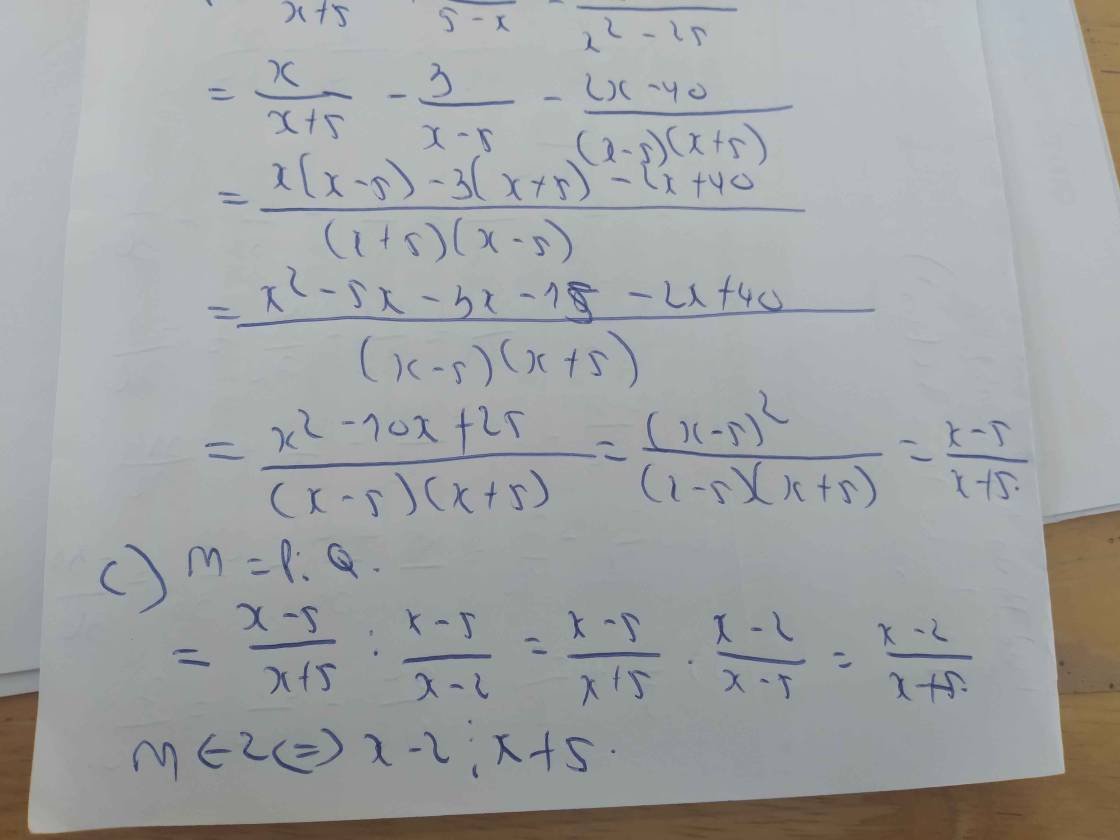giúp mik câu b với!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Sửa đề; TÌm giá trị nhỏ nhất của A
\(A=3x^2-6x+8\)
\(=3x^2-6x+3+5\)
\(=3\left(x^2-2x+1\right)+5=3\left(x-1\right)^2+5>=5\forall x\)
Dấu '=' xảy ra khi x-1=0
=>x=1
b: \(B=-2x^2-6x+7\)
\(=-2\left(x^2+3x-\dfrac{7}{2}\right)\)
\(=-2\left(x^2+3x+\dfrac{9}{4}-\dfrac{23}{4}\right)\)
\(=-2\left(x+\dfrac{3}{2}\right)^2+\dfrac{23}{2}< =\dfrac{23}{2}\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{3}{2}=0\)
=>\(x=-\dfrac{3}{2}\)
Đầu tiên cần chuyển biểu thức \(A\) về dạng hoàn chỉnh của một hàm số bậc hai. đỉnh của parabol nằm ở \(x = -\frac{b}{2a}\). => \(a = 3\), \(b = -6\). Do đó:
$$x_{\text{đỉnh}} = -\frac{-6}{2 \cdot 3} = 1.$$
Để tìm giá trị lớn nhất của \(A\), ta thay \(x = 1\) vào biểu thức \(A\):
$$A = 3 \cdot (1)^2 - 6 \cdot 1 + 8 = 3 - 6 + 8 = 5.$$
Vậy giá trị lớn nhất của \(A\) là \(5\) và đạt được khi \(x = 1\).
Đỉnh của parabol \(B\) nằm ở \(x = -\frac{b}{2a}\). Trong trường hợp này, \(a = -2\), \(b = -6\). Do đó:
$$x_{\text{đỉnh}} = -\frac{-6}{2 \cdot (-2)} = -\frac{-6}{-4} = \frac{3}{2}.$$
Thay \(x = \frac{3}{2}\) vào biểu thức \(B\):
$$B = 7 - 2 \cdot \left(\frac{3}{2}\right)^2 - 6 \cdot \frac{3}{2} = 7 - 2 \cdot \frac{9}{4} - 9 = 7 - \frac{9}{2} - 9 = 7 - \frac{9 + 18}{2} = 7 - \frac{27}{2} = \frac{14 - 27}{2} = -\frac{13}{2}.$$
Vậy giá trị lớn nhất của \(B\) là \(-\frac{13}{2}\) và đạt được khi \(x = \frac{3}{2}\).