b, 5x(x+1)-2(3x+1)-(7-x)  

= \(5x^2+5x-6x-2-7+x\)-x

=\(5x^2-2x-9\)

c, (2x-3)(3x+5)-(x-1) (6x+2)+3-5x

=\(6x^2+10x-9x-15-6x^2-2+6x+2+3-5x\)

=-10x-12

=5x+6

Trong ∆ ABC ta có: E là trung điểm của cạnh AB

D là trung điểm của cạnh AC

Nên ED là đường trung bình của  ∆ ABC

⇒ ED // BC và ED = 1/2 BC

(tính chất đường trung bình của tam giác)

+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.

Trong hình thang BCDE, ta có: BC // DE

M là trung điểm cạnh bên BE

N là trung điểm cạnh bên CD

Nên MN là đường trung hình hình thang BCDE ⇒ MN // DE

(tính chất đường trung bình hình thang)

Trong  ∆ BED, ta có: M là trung điểm BE

Nhận thấy ED đường trung bình tam giác ABC (AE = EB ; AD = DC)

=> ED = 1/2 BC(1) ; ED // BC (2)

Lại có EM = MB ; DN = NC ; ED//BC 

=> MN là đường trung bình hình thang ABCD 

=> MN // BC//ED 

Xét tam giác MEK và tam giác EBC có 

ME = MB ; MK//BC 

=> EK = KC  

=> MK = 1/2 BC = DE 

Xét tam giác MBI và tam giác EBD CÓ 

MB = ME ; MI//ED 

=> MI = 1/2 ED (3)

Xét tam giác KNC và tam giác EDC có 

EK = KC ; DN = NC 

=> KN = 1/2 ED (4)

Lại có IK = MK - MI = ED - 1/2 ED = 1/2 ED (5)

Từ (3)(4)(5) => MI = IK = KN

Kẻ MF // BE , mà D $\in$ BE nên DE // MF .

Xét $\Delta$AMF có :

AD = DM (gt) ; DE // MF

$\Rightarrow$ AE = EF (1) .

Xét $\Delta$CBE có :

BM = CM ; MF // BE

$\Rightarrow$ EF = FC (2) .

Từ (1) và (2) có :AE = 1/2(EF + FC) (3)

Có EF + FC = EC (4) .

Từ (3) và (4) $\Rightarrow$ AE = 1/2EC .

Vậy AE = 1/2 EC ( đpcm ) .

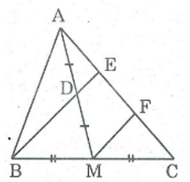
Gọi F là trung điểm của EC.

Trong ΔCBE, ta có:

M là trung điểm của CB;

F là trung điểm của CE.

Nên MF là đường trung bình của ΔCBE

⇒ MF// BE (tính chất đường trung bình của tam giác) hay DE// MF

* Trong ΔAMF, ta có: D là trung điểm của AM

DE // MF

Suy ra: AE = EF (tính chất đường trung bình của tam giác)

Mà EF = FC = EC/2 nên AE = 1/2 EC

* Trong ΔABC, ta có:

E là trung điểm của AB (gt)

D là trung điểm của AC (gt)

Nên ED là đường trung bình của ΔABC

⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)

* Trong ΔGBC, ta có:

I là trung điểm của BG (gt)

K là trúng điểm của CG (gt)

Nên IK là đường trung bình của ΔGBC

⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)

Từ (l) và (2) suy ra: IK // DE, IK = DE.

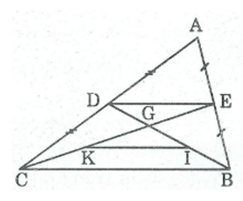
* Trong ΔABC, ta có:

E là trung điểm của AB (gt)

D là trung điểm của AC (gt)

Nên ED là đường trung bình của ΔABC

⇒ ED//BC và ED = BC/2 (tính chất đường trung bình của tam giác) (l)

* Trong ΔGBC, ta có:

I là trung điểm của BG (gt)

K là trúng điểm của CG (gt)

Nên IK là đường trung bình của ΔGBC

⇒ IK // BC và IK = BC/2 (tỉnh chất đường trung bình của tam giác) (2)

Từ (l) và (2) suy ra: IK // DE, IK = DE.

Xét tam giác ABD có: M là trung điểm của AD; MI // AB
=> I là trung điểm của DB
=> MI là đường trung bình của tam giác ABD => MI = AB/2 = 6/2 = 3cm

Xét tam giác CAB có: N là trung điểm của BC;
NK //AB => K là trung điểm của AC
=> NK là đường trung bình của tam giác ABC
=> NK = AB / 2 = 6/2 = 3 cm
+) MN = MI + IK + KN = 3 + IK + 3 = 6 + IK = 10 => IK = 4 cm

Xét tam giác ADC  có AE = ED ; AI = IC 

=> EI đường trung bình tam giác ADC

=> EI//DC (1) ; EI = 1/2 DC (2)

Tương tự : IF đường trung bình tam giác ABC 

=> IF = 1/2 AB (3) ; IF//AB (4) 

Từ (1)(4) => Đpcm

b) Xét tam giác IEF có : EI + IF > EF (5)

Từ (2);(3) ; (5)

=> \(EI+IF=\frac{AB+CD}{2}>EF\)(6)

Nhận thấy (AB + CD) : 2 = EF <=> EF//AB//CD 

Khi đó EF là đường trung bình hình thang ABCD

=> (AB + CD) : 2 = EF (7)

Từ (6);(7) => ĐPCM (Dấu "=" xảy ra <=> AB//CD//EF)

Gọi số tiền lãi của anh Minh là a (triệu) (0 < a < 58)

số tiền lãi của anh Quang là 58 - a (triệu)

=> Tỉ lệ giữa tiền lãi và tiền đã góp của anh Minh : \(\frac{a}{150}\)

Tỉ lệ giữa tiền lãi và tiền đã góp của anh Quang : \(\frac{58-a}{140}\)

Vì tỉ lệ tiền góp vói tiền lãi của 2 anh là như nhau 

=> \(\frac{a}{150}=\frac{58-a}{140}\)

=> (58 - a).150 = 140.a

<=> 58.150 - 150a = 140a

<=> 8700 = 290a

<=> a = 30(tm)

=> 58 - a = 28 (tm)

Vậy số tiền lãi của Anh Minh là 30 triệu ;số tiền lãi của anh Quang là 28 triệu 

Gọi số học sinh khối 8 là a (\(a\inℕ^∗;a>10\))

=> số học sinh khối 9 là a - 10 

=> Số cây khối 8 trồng là 8a

=> Số cây khối 9 trồng là 9(a - 10) = 9a - 90

mà số cây 2 khối trồng là như nhau nên ta có 

8a = 9a - 90

<=> a = 90

Số cây mỗi khối trồng được là 90 x 8 = 720 cây

|3 - 2x| - 7 = 0

<=> |3 - 2x| = 7

<=> \(\orbr{\begin{cases}3-2x=7\\3-2x=-7\end{cases}}\Leftrightarrow\orbr{\begin{cases}-2x=4\\-2x=-10\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=5\end{cases}}\)

Vậy \(x\in\left\{-2;5\right\}\)là nghiệm phương trình 

=> 3 - 2x - 7 = 0

     2x - 7         = 3

     2x               = 3+7

     2x               = 10

       x               = 10 : 2

      x                =5

Vậy x = 5