Gọi a là số kỳ thủ tham gia (a thuộc N*)

Hai kỳ thủ bất kỳ gặp nhau hai ván gồm trận lượt đi và lượt về khi đó số trận đấu là

a(a-1)=90

→a=10(tm) hoặc a=-9(không tm)

=>Vậy số kỳ thủ tham gia là 10 người.

Tuổi con hiện nay là \(48\times\dfrac{1}{4}=12\left(tuổi\right)\)

Tuổi mẹ hiện nay là 48-12=36(tuổi)

3/5 số năm nữa để tuổi con bằng 2/5 tuổi mẹ là:

\(\dfrac{2}{5}\times36-12=14,4-12=2,4\)

=>Số năm nữa để tuổi con bằng 2/5 tuổi mẹ là:

2,4:0,6=4(năm)

Nửa chu vi hình chữ nhật:

48 : 2 = 24 (m)

Tổng chiều dài và chiều rộng lúc sau:

24 - 2 + 4 = 26 (m)

Tổng số phần bằng nhau:

6 + 7 = 13 (phần)

Chiều dài mới là:

26 : 13 × 7 = 14 (m)

Chiều dài ban đầu là:

14 + 2 = 16 (m)

Chiều rộng ban đầu là:

24 - 16 = 8 (m)

Diện tích ban đầu là:

16 × 8 = 128 (m²)

Giai

Nửa chu vi hình chữ nhật là :

        48:2=24(m)

Tổng chiều dài và chiều rộng sau khi tăng và giảm là:

        24-2+4=26(m) 

Ta có sơ đồ:

Chiều rộng : 6 phần

Chiều dài : 7 phần

Chiều rộng ban đầu là: 

      26:(6+7)x 6-4=8(m) 

Chiều dài ban đầu là :

      26:(6+7)x7+2=16(m)

Diện tích hình chữ nhật là 

       16x8=128(m2)

                   Đ/S

Theo đề bài, ta có:

(7 + x)/15 = 2/3

7 + x = 2/3 × 15

7 + x = 10

x = 10 - 7

x = 3

Vậy x = 3

<

<

a) Ta có:

x² ≥ 0 với mọi x ∈ R

⇒ x² + 4 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

b) Ta có:

⇒ (x - 1)² ≥ 0 với mọi x ∈ R

≺ (x - 1)² + 7 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

c) x² + 2x + 2

= x² + x + x + 1 + 1

= (x² + x) + (x + 1) + 1

= x(x + 1) + (x + 1) + 1

= (x + 1)(x + 1) + 1

= (x + 1)² + 1

Ta có:

(x + 1)² ≥ 0 với mọi x ∈ R

⇒ (x + 1)² + 1 > 0 với mọi x ∈ R

Vậy đa thức đã cho không có nghiệm

34/15 x 3/17

= 2/5 x 1

= 2/5

3/19 : 6/57

= 3/19 x 57/6

= 1/19 x 57/2

= 57/38

3/16 + 14/32

= 3/16 + 7/16

= 10/16 = 5/8

9/21 - 2/7

= 3/7 - 2/7

= 1/7

\(\dfrac{34}{15}\times\dfrac{3}{17}=\dfrac{34\times3}{15\times17}=\dfrac{2}{5}\)

\(\dfrac{3}{19}:\dfrac{6}{57}=\dfrac{3}{19}\times\dfrac{57}{6}=\dfrac{3\times57}{19\times6}=\dfrac{3}{2}\)

\(\dfrac{3}{16}+\dfrac{14}{32}=\dfrac{6}{32}+\dfrac{14}{32}=\dfrac{6+14}{32}=\dfrac{20}{32}=\dfrac{5}{8}\)

\(\dfrac{9}{21}-\dfrac{2}{7}=\dfrac{9}{21}-\dfrac{6}{21}=\dfrac{9-6}{21}=\dfrac{3}{21}=\dfrac{1}{7}\)

`#NqHahh`

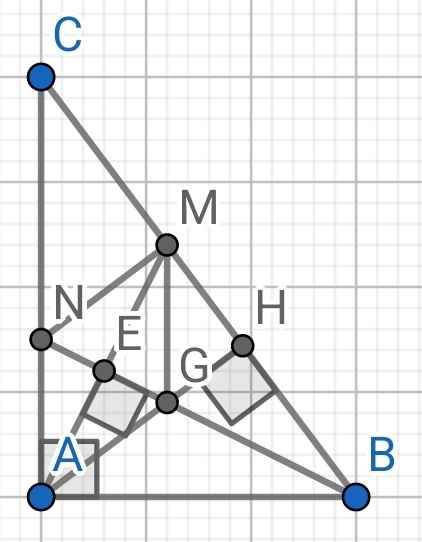
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:

BA = BM (gt)

BE là cạnh chung

⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)

b) Do ∆ABE = ∆MBE (cmt)

⇒ ∠ABE = ∠MBE (hai góc tương ứng)

⇒ ∠ABN = ∠MBN

Xét ∆ABN và ∆MBN có:

BA = BM (gt)

∠ABN = ∠MBN (cmt)

BN là cạnh chung

⇒ ∆ABN = ∆MBN (c-g-c)

⇒ AN = MN (hai cạnh tương ứng)

c) Do ∆ABN = ∆MBN (cmt)

⇒ ∠BAN = ∠BMN (hai góc tương ứng)

Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)

⇒ ∠BMN = 90⁰

⇒ MN ⊥ BM

⇒ MN ⊥ BC

Lại có AH là đường cao của ∆ABC (gt)

⇒ AH ⊥ BC

Mà MN ⊥ BC (cmt)

⇒ AH // MN

⇒ ∠MGN = ∠ANG (so le trong)

Cho tam giác ABC vuông tại A ( AB < AC ). Trên tia đối của tia AB, lấy điểm D sao cho AB = AD

a) Chứng minh tam giác ACB = tam giác ACD từ đó suy ra tam giác BCD cân.

b) Gọi E, F lần lượt là trung điểm của CD và BC, BE cắt CA tại I. Chứng minh, D, I, F thẳng hàng.

c) Kẻ đường thẳng qua D, song song BC và cắt BE tại M. Gọi G là giao điểm của MA và CD. Chứng minh BC = 6GF

Giúp tui câu này nha 🥺