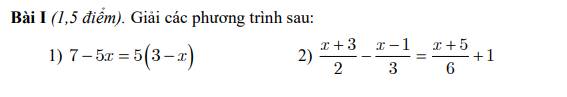Câu 5. (3 điểm) Cho ΔABC nhọn (AB < AC). Hai đường cao BE và CF cắt nhau tại H. a) Chứng minh: ΔABE ∽ ΔACF b) Chứng minh: 𝐴𝐸𝐹 ̂=𝐴𝐵𝐶 ̂ c) Gọi K là trung điểm của BC, đường thẳng vuông góc với HK tại H cắt AB và AC lần lượt tại P và Q. Chứng minh: HP = HQ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

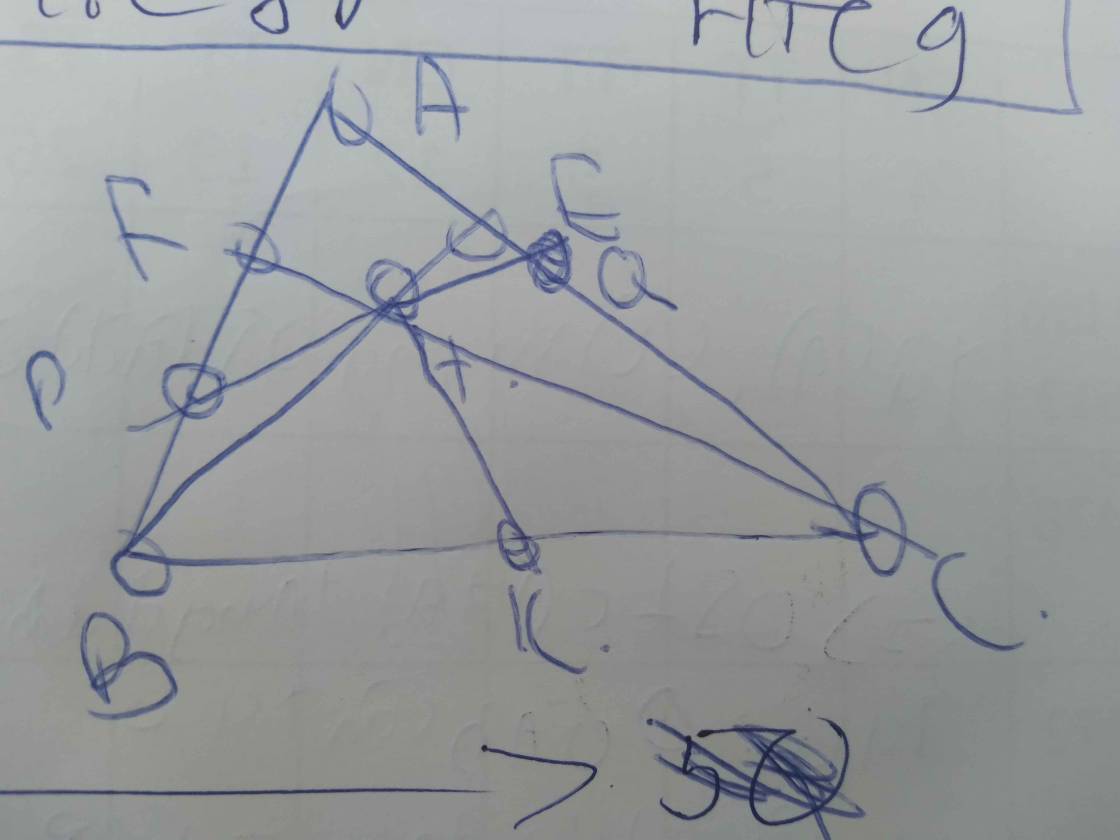


a) Đồ thi của hàm số đi qua điểm \(B\left(3;-2\right)\) thay các giá trị x và y tương ứng vào ta có:
\(-2=\left(2m-1\right)\cdot3+1\)
\(\Leftrightarrow3\left(2m-1\right)=-3\)
\(\Leftrightarrow2m-1=-1\)
\(\Leftrightarrow2m=0\)
\(\Leftrightarrow m=0\left(tm\right)\)
b) Với `m=0` thì ta có hàm số: \(y=\left(2\cdot0-1\right)x+1\Rightarrow y=-x+1\)
Vẽ:
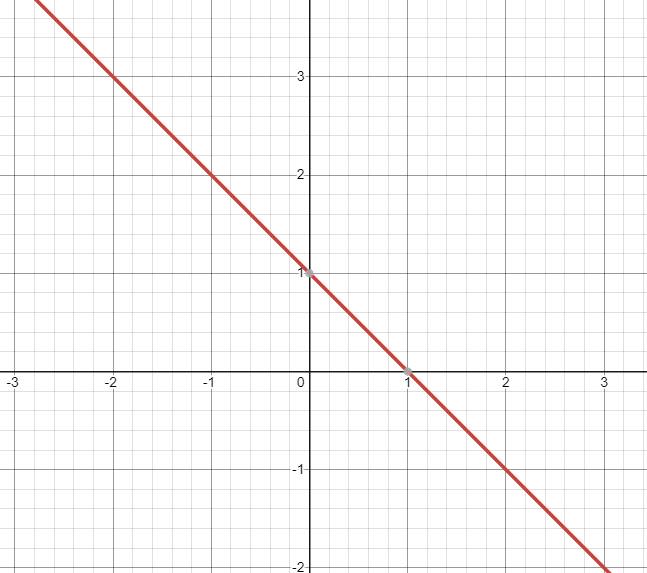

1) \(7-5x=5\left(3-x\right)\)
\(\Leftrightarrow7-5x=15-5x\)
\(\Leftrightarrow-5x+5x=15-7\)
\(\Leftrightarrow0=8\) (vô lý)
Phương trình vô nghiệm
2) \(\dfrac{x+3}{2}-\dfrac{x-1}{3}=\dfrac{x+5}{6}+1\)
\(\Leftrightarrow\dfrac{3\left(x+3\right)}{6}-\dfrac{2\left(x-1\right)}{6}=\dfrac{x+5}{6}+\dfrac{6}{6}\)
\(\Leftrightarrow3\left(x+3\right)-2\left(x-1\right)=x+5+6\)
\(\Leftrightarrow3x+9-2x+2=x+11\)
\(\Leftrightarrow x+11=x+11\)
\(\Leftrightarrow x-x=11-11\)
\(\Leftrightarrow0=0\) (luôn đúng)
Vậy phương trình có vô số nghiệm

Gọi chiều rộng là x(m)
(ĐIều kiện: x>0)
NỬa chu vi miếng đất là 60:2=30(m)
Chiều dài miếng đất là 30-x(m)
Bốn lần chiều rộng bằng 2 lần chiều dài nên ta có:
4x=2(30-x)
=>4x=60-2x
=>6x=60
=>x=10(nhận)
Vậy: Chiều rộng là 10m; chiều dài là 30-10=20m
Diện tích miếng đất là \(10\cdot20=200\left(m^2\right)\)

Xét ΔABC có
M,N lần lượt là trung điểm của BC,BA
=>MN là đường trung bình của ΔABC
=>MN//AC
=>MN\(\perp\)AB tại N
Xét ΔINB vuông tại N và ΔIBM vuông tại B có
\(\widehat{NIB}\) chung
Do đó: ΔINB~ΔIBM
=>\(\dfrac{IN}{IB}=\dfrac{IB}{IM}\)
=>\(IN\cdot IM=IB^2\)

Gọi độ dài quãng đường AB là x(km)
(ĐK: x>0)
Thời gian ô tô đi từ A đến B là \(\dfrac{x}{50}\left(giờ\right)\)
Thời gian ô tô đi từ B về A là \(\dfrac{x}{40}\left(giờ\right)\)
Tổng thời gian cả đi lẫn về là 9 giờ nên \(\dfrac{x}{40}+\dfrac{x}{50}=9\)
=>\(\dfrac{9}{200}\cdot x=9\)
=>x=200(nhận)
Vậy: Độ dài AB là 200km

Gọi số lượng bộ quần áo anh Minh đặt hàng là x(bộ)
(ĐK: \(x\in Z^+\))
Thời gian dự kiến hoàn thành là \(\dfrac{x}{100}\left(ngày\right)\)
Số bộ áo thực tế anh Minh có được là x+60(bộ)
Thời gian thực tế hoàn thành là \(\dfrac{x+60}{120}\left(ngày\right)\)
Cửa hàng giao hàng sớm 3 ngày nên ta có:
\(\dfrac{x}{100}-\dfrac{x+60}{120}=3\)
=>\(\dfrac{6x-5\left(x+60\right)}{600}=3\)
=>x-300=1800
=>x=2100(nhận)
vậy: số lượng bộ quần áo anh Minh đặt hàng là 2100 bộ

Thay tọa độ điểm B vào hàm số, ta có:
-m + 4 = 2
-m = 2 - 4
-m = -2
m = 2