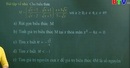Áp dụng bổ đề quen thuộc \(x^3+y^3\ge xy\left(x+y\right)\), ta được: \(\frac{1}{2a^3+b^3+c^3+2}=\frac{1}{\left(a^3+b^3\right)+\left(a^3+c^3\right)+2}\le\frac{1}{ab\left(a+b\right)+ac\left(a+c\right)+2}\)\(=\frac{bc}{ab^2c\left(a+b\right)+abc^2\left(a+c\right)+2bc}=\frac{bc}{b\left(a+b\right)+c\left(a+c\right)+2bc}\)\(\le\frac{bc}{ab+ac+4bc}=\frac{bc}{b\left(a+c\right)+c\left(a+b\right)+2bc}\)\(\le\frac{1}{9}\left(\frac{bc}{b\left(a+c\right)}+\frac{bc}{c\left(a+b\right)}+\frac{bc}{2bc}\right)=\frac{1}{9}\left(\frac{c}{a+c}+\frac{b}{a+b}+\frac{1}{2}\right)\)(1)

Tương tự, ta có: \(\frac{1}{a^3+2b^3+c^3+2}\le\frac{1}{9}\left(\frac{c}{b+c}+\frac{a}{a+b}+\frac{1}{2}\right)\)(2); \(\frac{1}{a^3+b^3+2c^3+2}\le\frac{1}{9}\left(\frac{b}{b+c}+\frac{a}{a+c}+\frac{1}{2}\right)\)(3)

Cộng theo vế ba bất đẳng thức (1), (2), (3), ta được: \(P\le\frac{1}{9}\left(1+1+1+\frac{3}{2}\right)=\frac{1}{2}\)

Vậy giá trị lớn nhất của P là \(\frac{1}{2}\)đạt được khi x = y = z = 1

Đặt số ghế là x; số học sinh là y ta có hệ phương trình

\(\hept{\begin{cases}4x=y-6\\\frac{y}{5}=x-1\end{cases}}\)

Bạn tự giải nốt hệ nhé

ĐKXĐ : \(\hept{\begin{cases}x\ge\frac{1}{2}\\y\ge-\frac{2}{3}\end{cases}}\)

Đặt \(\hept{\begin{cases}\sqrt{2x-1}=a\\\sqrt{3y+2}=b\end{cases}\left(a,b\ge0\right)}\)

Ta có hệ phương trình \(\hept{\begin{cases}a+b=2\\3a-2b=1\end{cases}}\)( giải hệ như này thì đơn giản rồi mình k trình bày cách làm :) )

=> a = b = 1 ( tm )

=> \(\hept{\begin{cases}\sqrt{2x-1}=1\\\sqrt{3y+2}=1\end{cases}}\Rightarrow\hept{\begin{cases}2x-1=1\\3y+2=1\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=-\frac{1}{3}\end{cases}}\left(tm\right)\)

Vậy phương trình có 1 nghiệm duy nhất \(\hept{\begin{cases}x=1\\y=-\frac{1}{3}\end{cases}}\)

x² - 2( 3m + 2 )x + 2m² + 3m + 5 = 0

Để phương trình có nghiệm kép thì Δ = 0

=> [ -2( 3m + 2 ) ]² - 4( 2m² + 3m + 5 ) = 0

<=> 4( 3m + 2 )² - 8m² - 12m - 20 = 0

<=> 4( 9m² + 12m + 4 ) - 8m² - 12m - 20 = 0

<=> 36m² + 48m + 16 - 8m² - 12m - 20 = 0

<=> 28m² + 36m - 4 = 0

<=> 7m² + 9m - 1 = 0 (*)

Δ = b² - 4ac = 9² - 4.7.(-1) = 81 + 28 = 109

Δ > 0 nên (*) có hai nghiệm phân biệt

\(\hept{\begin{cases}m_1=\frac{-b+\sqrt{\text{Δ}}}{2a}=\frac{-9+\sqrt{109}}{14}\\m_2=\frac{-b-\sqrt{\text{Δ}}}{2a}=\frac{-9-\sqrt{109}}{14}\end{cases}}\)

Vậy với \(m=\frac{-9\pm\sqrt{109}}{14}\)thì phương trình có nghiệm kép

Ta có:

\(\Delta^'=\left(3m+2\right)^2-\left(2m^2+3m+5\right)\)

\(=9m^2+12m+4-2m^2-3m-5\)

\(=7m^2+9m-1\)

Để PT có nghiệm kép thì \(\Delta^'=0\)

\(\Leftrightarrow7m^2+9m-1=0\)

\(\Delta_m=9^2-4\cdot7\cdot\left(-1\right)=109\)

\(\Rightarrow m=\frac{-9\pm\sqrt{109}}{14}\)

Vậy khi \(m=\frac{-9\pm\sqrt{109}}{14}\) thì PT có nghiệm kép