Có ai k6 ko ? kb làm wen nha ! 2+3= mấy
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1 + 1 = 2
2 + 2 = 4
4 + 4 = 5
5 + 5 = 6
6 + 6 = 7
7 + 7 = 8
8 + 8 = 9
9 + 9 = 10
đùa đéi bạn mik sẽ kb với bạn

* Với \(m=-2\) thì phương trình đã cho là phương trình bậc nhất một ẩn và chỉ có một nghệm duy nhất
* Với \(m\ne-2\) thì phương trình đã cho là phương trình bậc hai một ẩn.
\(\Delta'=m^2-\left(m+2\right)\times1=m^2-m-2\)
TH1: \(\Delta'< 0\Leftrightarrow m^2-m-2< 0\Leftrightarrow-1< m< 2\) thì phương vô nghiệm
TH2: \(\Delta'=0\Leftrightarrow m^2-m-2=0\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=2\end{matrix}\right.\) thì phương trình có nghiệm kép
TH3: \(\Delta'>0\Leftrightarrow m^2-m-2>0\Leftrightarrow\left[{}\begin{matrix}-\infty\le m< -1\\2< m\le+\infty\end{matrix}\right.\) thì phương trình có hai nghiệm phân biệt
Vậy: Với \(m=-2\) thì phương trình đã cho có 1 nghiệm duy nhất
\(-1< m< 2\) thì phương trình đã cho vô nghiệm
\(m=-1\) hoặc \(m=2\) thì phương trình đã cho có nghiệm kép
\(-\infty\le m< -1\) và \(m\ne-2\)hoặc \(2< m\le+\infty\) thì phương trình đã cho có hai nghiệm phân biệt

b) Ta có \(\left(x-a\right)\left(x-b\right)+\left(x-b\right)\left(x-c\right)+\left(x-c\right)\left(x-a\right)=0\)(*)
\(\Leftrightarrow3x^2-2\left(a+b+c\right)x+ab+bc+ca=0\)là phương trình bậc 2
\(\Delta'=\left(a+b+c\right)^2-3\left(ab+bc+ca\right)=a^2+b^2+c^2-ab-bc-ca\)
\(=\frac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)
vậy phương trình (*) luôn có nghiệm
c) Xét \(\Delta=\left(a+b\right)^2+8\left(a^2-ab+b^2\right)\)
Xét \(\left(a+b\right)^2\ge0\)
\(8\left[\left(a^2-2a+\frac{1}{2}b+\frac{b^2}{4}\right)+\frac{3b^2}{4}\right]=8\left[\left(a-\frac{1}{2}b\right)^2+\frac{3b^2}{4}\right]>0\forall a,b\)
\(\Delta>0\forall a,b\)=> phương trình có 2 nghiệm phân biệt với mọi a,b (đpcm)
*em thấy câu a) và b) same same nhau
@Linh: Câu c) bạn chỉ cần xét tích \(-2\left(a^2-ab+b^2\right).1< 0\) chứ không cần tính hẳn \(\Delta\) ra cũng được.

( m + 1 )x2 - 2x + ( m - 1 ) = 0
ĐKXĐ : m khác -1
Để phương trình có nghiệm thì Δ ≥ 0
=> ( -2 )2 - 4( m + 1 )( m - 1 ) = 0
<=> 4 - 4( m2 - 1 ) = 0
<=> 4 - 4m2 + 4 = 0
<=> -4m2 + 8 = 0
<=> m2 - 2 = 0
<=> ( m - √2 )( m + √2 ) = 0
<=> m = ±√2
Vậy với m = ±√2 thì phương trình có nghiệm
TH1: a=0 ⇔ (m+1) = 0 ⇔ m = -1. Khi đó phương trình đã cho là:
-2x - 2 = 0 ⇔ x = 1
TH2: a ≠ 0 ⇔ m + 1 ≠ 0 ⇔ m ≠ -1
Phương trình có nghiệm khi và chỉ khi △' ≥ 0
⇔ 1 - (m+1)(m-1) ≥ 0 ⇔ -m2 + 2 ≥ 0 ⇔ \(-\sqrt{2}\le m\le\sqrt{2}\)
KL: Kết hợp cả hai trường hợp ta được: \(-\sqrt{2}\le m\le\sqrt{2}\)

m( m - 2 )x2 - 2mx + 3 = 0
ĐKXĐ : m ≠ 0 hoặc m ≠ 2
Để phương trình vô nghiệm thì Δ < 0
tức là ( -2m )2 - 12m( m - 2 ) < 0
<=> 4m2 - 12m2 + 24m < 0
<=> -8m2 + 24m < 0
<=> m2 - 3m < 0
<=> m( m - 3 ) < 0
Xét hai trường hợp :
1) \(\hept{\begin{cases}m>0\\m-3< 0\end{cases}}\Rightarrow\hept{\begin{cases}m>0\\m< 3\end{cases}}\Rightarrow\hept{\begin{cases}0< m< 3\\m\ne2\end{cases}}\)
2) \(\hept{\begin{cases}m< 0\\m-3>0\end{cases}}\Rightarrow\hept{\begin{cases}m< 0\\m>3\end{cases}}\)( loại )
Vậy với \(\hept{\begin{cases}0< m< 3\\m\ne2\end{cases}}\)thì phương trình vô nghiệm

( m + 1 )x2 - 2mx + ( m + 2 ) = 0
ĐKXĐ : m khác -1
Để phương trình có hai nghiệm phân biệt thì Δ > 0
tức là ( -2m )2 - 4( m + 1 )( m + 2 ) > 0
<=> 4m2 - 4( m2 + 3m + 2 ) > 0
<=> 4m2 - 4m2 - 12m - 8 > 0
<=> -12m > 8
<=> m < -2/3
Vậy với m < -2/3 thì phương trình có hai nghiệm phân biệt
(m+1)x^2-2mx+(m+2) = 0(m+1)x22−2mx+(m+2)=0 (Đk :m≠-1)
Để phương trình có 2 nghiệm phân biệt thì Δ>0
<=> (-2m)2 -4(m+1)(m+2) >0
<=> 4m2-4(m2 +3m+2) >0
<=> 4m2 -4m2 -12m -8 >0
<=> -12m>8
<=> m<-2/3
vậy với m<-2/3 thì phương trình có 2 nghiệm phân biệt



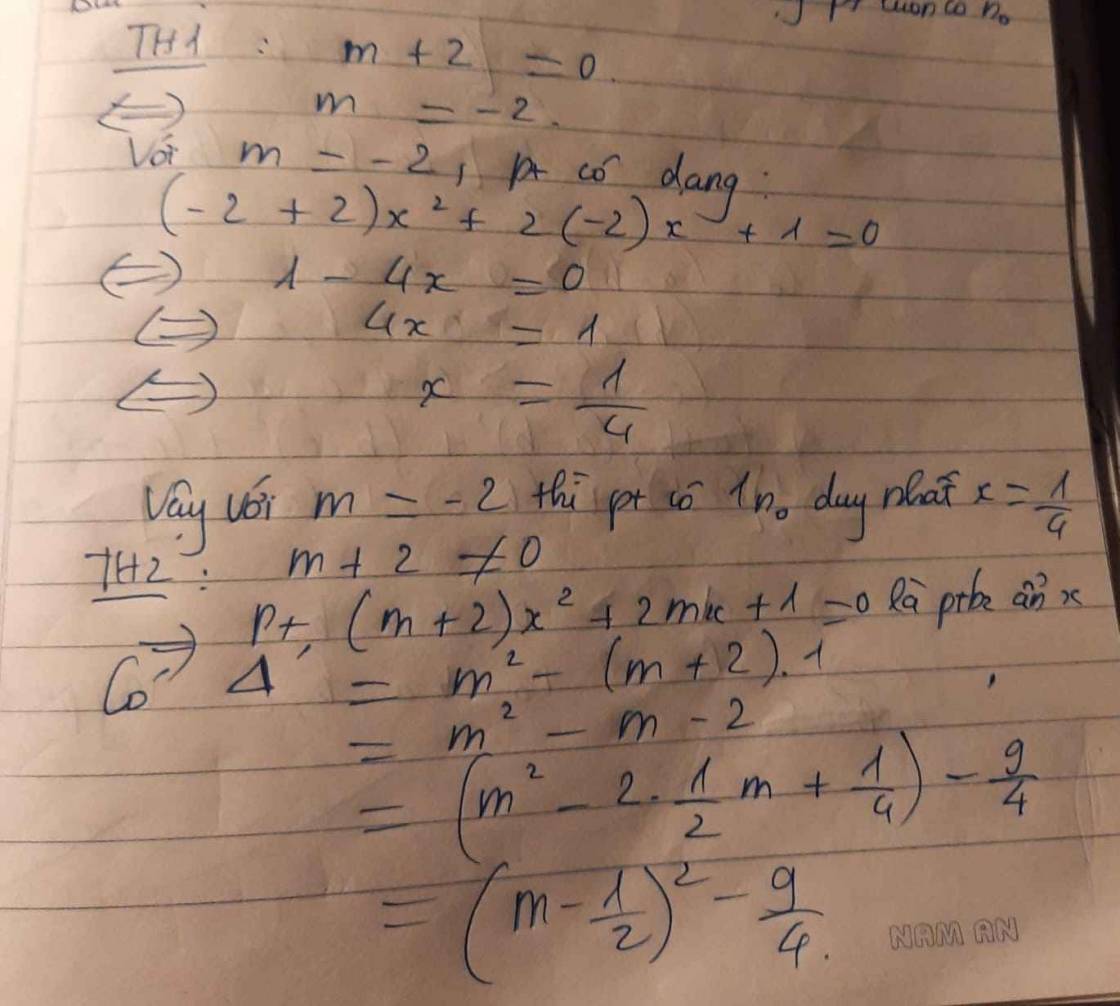

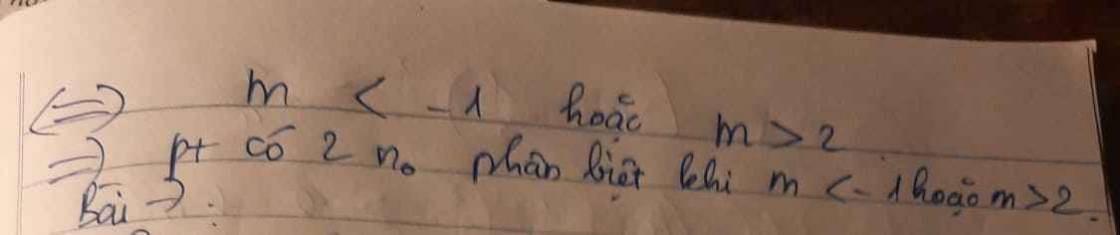
hi kb nha