Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{99^2}+\dfrac{1}{100^2}=\\ A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{99.99}+\dfrac{1}{100.100}\\ A< \dfrac{1}{2.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\\ A< \dfrac{1}{2.2}+\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\right)\\ A< \dfrac{1}{2.2}+\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right)\\ A< \dfrac{1}{2.2}+\left(\dfrac{1}{2}-\dfrac{1}{100}\right)\\ A< \dfrac{1}{2.2}+\dfrac{49}{50}\\ A< \dfrac{1}{4}+\dfrac{49}{50}\\ A< \dfrac{37}{50}=\dfrac{74}{100}< \dfrac{75}{100}=\dfrac{3}{4}\) Hay \(A< \dfrac{3}{4}\)

Vậy \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{99^2}+\dfrac{1}{100^2}< \dfrac{3}{4}\)

a) Số học sinh loại giỏi:

120 . 1/6 = 20 (học sinh)

Số học sinh khá:

120 . 30% = 36 (học sinh)

Số học sinh trung bình:

120 . 1/3 = 40 (học sinh)

Số học sinh yếu:

120 - 20 - 36 - 40 = 24 (học sinh)

b) Tỉ số phần trăm của số học sinh yếu so với cả lớp:

24 . 100% : 120 = 20%

Chiều dài mảnh đất:

13,7 × 4 = 54,8 (m)

Diện tích mảnh đất:

54,8 × 13,7 = 750,76 (m²)

Diện tích trang trại:

71,769 × 4 = 287,076 (m²)

Diện tích còn thừa:

750,76 - 71,769 - 287,076 = 391,915 (m²)

Đây ạ !

Chiều dài của mảnh đất hình chữ nhật là:

13,7 x 4= 54,8 (m)

Diện Tích của mảnh đất đó là :

54,8 × 13,7 = 750,76 (m²)

Diện tích của trang trại đó là:

71,769 × 4 = 287,076 (m²)

Diện tích mảnh đất còn thừa là :

750,76 - 71,769 - 287,076 = 391,915 (m²)

Đáp số : 391,915 m²

Số hộp sữa công ty đã chuyển trong hai đợt đầu:

4530 × 2 = 9060 (hộp)

Công ty còn phải chuyển thêm:

14964 - 9060 = 5904 (hộp)

a: Xét ΔMHN vuông tại H và ΔMHP vuông tại H có

MN=MP

MH chung

Do đó: ΔMHN=ΔMHP

b: Xét ΔIGM và ΔIEN có

IG=IE

\(\widehat{GIM}=\widehat{EIN}\)(hai góc đối đỉnh)

IM=IN

Do đó: ΔIGM=ΔIEN

=>\(\widehat{IGM}=\widehat{IEN}\)

=>MG//EN

Có 7 cách chọn chữ số hàng đơn vị

Có 6 cách chọn chữ số hàng chục

Có 5 cách chọn chữ số hàng trăm

Số số tự nhiên có thể lập được là:

5.6.7 = 210 (số)

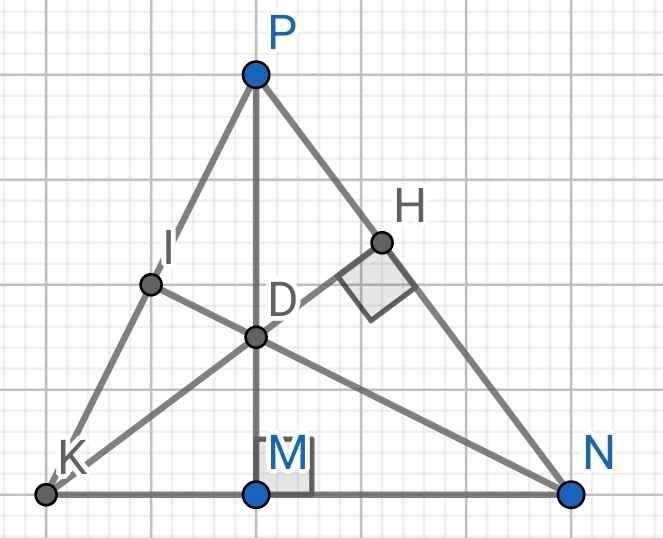
a) Do ND là đường phân giác của ∆MNP (gt)

⇒ ∠MND = ∠PND

⇒ ∠MND = ∠HND

Xét hai tam giác vuông: ∆MND và ∆HND có:

ND là cạnh chung

∠MND = ∠HND (cmt)

⇒ ∆MND = ∆HND (cạnh huyền - góc nhọn)

b) Do ∆MND = ∆HND (cmt)

⇒ MN = HN (hai cạnh tương ứng)

c) Do ∆MND = ∆HND (cmt)

⇒ MD = HD (hai cạnh tương ứng)

Xét hai tam giác vuông: ∆DMK và ∆DHP có:

MD = HD (cmt)

∠MDK = ∠HDP (đối đỉnh)

⇒ ∆DMK = ∆DHP (cạnh góc vuông - góc nhọn kề)

⇒ MK = HP (hai cạnh tương ứng)

Lại có: MN = HN (cmt)

⇒ MK + MN = HP + HN

⇒ KN = PN

⇒ ∆NPK cân tại N

Do ∆MNP vuông tại M (gt)

⇒ PM ⊥ MN

⇒ PM ⊥ NK

⇒ PM là đường cao của ∆NPK

Lại có:

DH ⊥ NP (gt)

⇒ KH ⊥ NP

⇒ KH là đường cao thứ hai của ∆NPK

⇒ ND là đường cao thứ ba của ∆NPK

Mà ∆NPK cân tại N (cmt)

⇒ ND cũng là đường trung tuyến của ∆NPK

⇒ ND đi qua trung điểm của PK

Mà I là trung điểm của PK

⇒ N, D, I thẳng hàng

a: A(x)+B(x)

\(=8x^4+8x^3-6x-15+8x^4+8x^3-4x^2-6x-10\)

\(=16x^4+16x^3-4x^2-12x-25\)

b: B(x)-A(x)

\(=8x^4+8x^3-4x^2-6x-10-8x^4-8x^3+6x+15\)

\(=-4x^2+5\)

c: \(C\left(x\right)\cdot\left(B\left(x\right)-A\left(x\right)\right)=\left(x+1\right)\left(-4x^2+5\right)\)

\(=-4x^3+5x-4x^2+5\)

a: Xét ΔDHE và ΔDHF có

DH chung

HE=HF

DE=DF

Do đó: ΔDHE=ΔDHF

b: Sửa đề HK\(\perp\)DF tại K

ΔDHE=ΔDHF

=>\(\widehat{HDE}=\widehat{HDF}\)

Xét ΔDMH vuông tại M và ΔDKH vuông tại K có

DH chung

\(\widehat{MDH}=\widehat{KDH}\)

Do đó: ΔDMH=ΔDKH

=>HM=HK

=>ΔHMK cân tại H

c: ΔDMH=ΔDKH

=>DM=DK

=>D nằm trên đường trung trực của MK(1)

Ta có: HM=HK

=>H nằm trên đường trung trực của MK(2)

Từ (1),(2) suy ra DH là đường trung trực của MK

=>DH\(\perp\)MK

A = 0,1 + 0,1² + 0,1³ + ... + 0,1⁹

A x 10 = 1 + 0,1 + 0,1² + ... + 0,1⁸

A x (10 - 1) = 1 - 0,1⁹

A x 9 = 1 - 0,000000001

A x 9 = 0,999999999

A = \(\dfrac{0,999999999}{9}=0,111111111\)