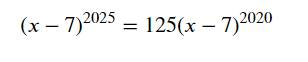Lời giải:

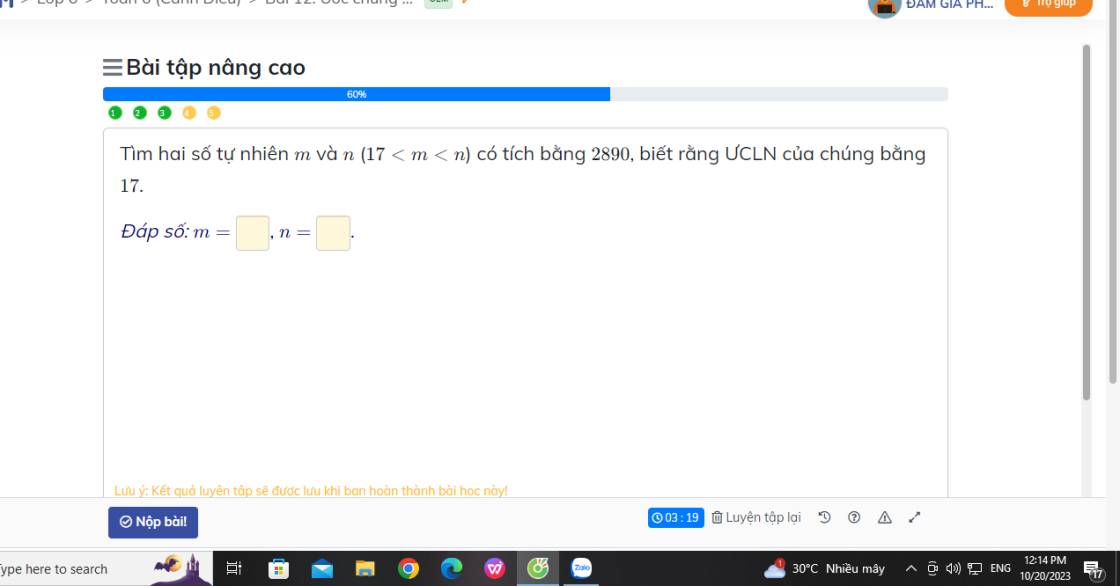
Vì ƯCLN(m,n) là $17$ và $17< m< n$ nên đặt $m=17a, n=17b$ với $1<a<b$ và $a,b$ là số tự nhiên, $(a,b)=1$.

Ta có:

$mn=2890$

$\Rightarrow 17a.17b=2890$

$\Rightarrow ab=10$

Mà $1< a< b$ và $(a,b)=1$ nên $a=2; b=5$

$\Rightarrow m=17a=17.2=34; n=17b=17.5=85$

2 số nguyên tố cùng nhau có ước chung lớn nhất là 1.

Gọi \(d=UCLN\left(n+4,2n+7\right)\)

Khi đó \(\left\{{}\begin{matrix}n+4⋮d\\2n+7⋮d\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2n+8⋮d\\2n+7⋮d\end{matrix}\right.\)

\(\Rightarrow\left(2n+8\right)-\left(2n+7\right)⋮d\)

\(\Rightarrow1⋮d\) hay \(d=1\) (dpcm)

\(\left(x-7\right)^{2025}=125\left(x-7\right)^{2020}\\ =>\left(x-7\right)^{2020}.\left[\left(x-7\right)^5-125\right]=0\)

\(=>\left[{}\begin{matrix}\left(x-7\right)^{2020}=0\\\left(x-7\right)^5=125\end{matrix}\right.\)

\(=>\left[{}\begin{matrix}x-7=0\\x-7=\sqrt[5]{125}\end{matrix}\right.\)

\(=>\left[{}\begin{matrix}x=7\\x=7+\sqrt[5]{125}\end{matrix}\right.\)

Lời giải:

$(x-7)^{2025}=125(x-7)^{2020}$

$\Rightarrow (x-7)^{2025}-125(x-7)^{2020}=0$

$\Rightarrow (x-7)^{2020}[(x-7)^5-125]=0$

$\Rightarrow (x-7)^{2020}=0$ hoặc $(x-7)^5=125$
$\Rightarrow x-7=0$ hoặc $x-7=sqrt[5]{125}+7$

Do p + 1 và p + 5 là số nguyên tố

Mà p + 5 là số lẻ

⇒ p là số chẵn

⇒ p = 2

Đây có phải phân số đâu bạn?

a) 200 = 2³.5²

300 = 2².3.5²

120 = 2³.3.5

ƯCLN(200; 300; 120) = 2².5 = 20

b) 60 = 2².3.5

80 = 2⁴.5

120 = 2³.3.5

ƯCLN(60; 80; 120) = 2².5 = 20

a)ƯCLN(200,300,120)= 20

b)ƯCLN(60,80,120)= 20

\(A=7^5:7^3+2\cdot3^2\)

\(A=7^{5-3}+2\cdot9\)

\(A=7^2+18\)

\(A=49+18\)

\(A=67\)

A = 7⁵ : 7³ + 2.3²

= 7² + 2.9

= 49 + 18

= 67

Theo đề bài: a - b = 6 nên ta có các tổ hợp a, b tương ứng: 
a = (6; 7; 8; 9) 
b = (0; 1; 2; 3) 
Thay các cặp a,b tương ứng ở trên vào n = 6a5 + 9b4 ta tìm được tổ hợp n tuơng ứng: 
n = (1569;1589;1609;1629) 
Vì n chia hết cho 9 nên ta chỉ có n = 1629 (a = 9; b = 3)

Do n ⋮ 9 nên:

⇒ 6 + a + 5 + 9 + b + 4 = (24 + a + b) ⋮ 9

⇒ a + b = 3 hoặc a + b = 12

*) a + b = 3 

a - b = 6

⇒ 2a = 9 (loại vì 2a chẵn)

*) a + b = 12

a - b = 6

⇒ 2a = 18

⇒ a = 18 : 2

⇒ a = 9

⇒ b = 12 - 9 = 3

Vậy a = 9; b = 3

Tạm dịch:

1) Susan có một giỏ táo. Có ít hơn 50 quả táo trong giỏ. Nếu cô ấy đưa cho mỗi người bạn 8 quả táo thì cô ấy sẽ không còn quả nào. Nếu cô ấy đưa cho mỗi người bạn 9 quả táo thì cô ấy sẽ cần thêm 5 quả táo nữa. Có bao nhiêu quả táo trong giỏ?

2) Lớp 6 môn GMaths có số học sinh bằng bội số của 5 từ 10 đến 2000. Có bao nhiêu học sinh lớp 6 môn GMaths?

đề 1) sai