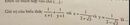
Áp dụng bđt svacxo, ta có: \(\frac{x_1^2}{y_1}+\frac{x_2^2}{y_2}+\frac{x_3^2}{y_3}\ge\frac{\left(x_1+x_2+x_3\right)^2}{y_1+y_2+y_3}\), ta có:

 \(\frac{4}{2a+b+c}+\frac{4}{2b+c+a}+\frac{4}{2c+a+b}\le4\cdot\frac{\left(1+1+1\right)^2}{4\left(a+b+c\right)}=\frac{9}{a+b+c}\) (1)

Áp dụng bđt: \(\frac{4}{x+y}\le\frac{1}{x}+\frac{1}{y}\), ta có:

 \(\frac{4}{2a+b+c}\le\frac{1}{a+b}+\frac{1}{a+c}\le\frac{1}{4}\cdot\left(\frac{2}{a}+\frac{1}{b}+\frac{1}{c}\right)\)

CMTT:: \(\frac{4}{2b+c+a}\le\frac{1}{4}\cdot\left(\frac{2}{b}+\frac{1}{a}+\frac{1}{c}\right)\)

  \(\frac{4}{2c+a+b}\le\frac{1}{4}\cdot\left(\frac{2}{c}+\frac{1}{a}+\frac{1}{b}\right)\)

=> \(\frac{4}{2a+b+c}+\frac{4}{2b+c+a}+\frac{4}{2c+a+b}\le\frac{1}{4}\cdot4.\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) (2)

Từ (1) và (2)

=> \(\frac{9}{a+b+c}\le\frac{4}{2a+b+c}+\frac{4}{2b+c+a}+\frac{4}{2c+a+b}\le\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)

Ta có: \(\frac{4}{2a+b+c}+\frac{4}{a+2b+c}+\frac{4}{a+b+2c}\)

\(\ge\frac{\left(2+2+2\right)^2}{2a+b+c+a+2b+c+a+b+2c}\)

\(=\frac{6^2}{4\left(a+b+c\right)}=\frac{36}{4\left(a+b+c\right)}=\frac{9}{a+b+c}\)

Lại có áp dụng BĐT Cauchy - Schwarz ngược:

\(\frac{4}{2a+b+c}=\frac{1}{4}\cdot\frac{16}{a+a+b+c}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=\frac{1}{4}\left(\frac{2}{a}+\frac{1}{b}+\frac{1}{c}\right)\)

Tương tự:

\(\frac{4}{a+2b+c}\le\frac{1}{4}\left(\frac{1}{a}+\frac{2}{b}+\frac{1}{c}\right)\) và \(\frac{4}{a+b+2c}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{2}{c}\right)\)

Cộng vế 3 BĐT trên lại ta được:
\(\frac{4}{2a+b+c}+\frac{4}{a+2b+c}+\frac{4}{a+b+2c}\le\frac{1}{4}\left(\frac{4}{a}+\frac{4}{b}+\frac{4}{c}\right)=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)

Dấu "=" xảy ra khi: a = b = c

Vậy \(\frac{9}{a+b+c}\le\frac{4}{2a+b+c}+\frac{4}{a+2b+c}+\frac{4}{a+b+2c}\le\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)

\(P=\frac{x\sqrt{x}-1}{1+x+\sqrt{x}}\cdot\left(\frac{\sqrt{x}+1}{x-1}-\frac{\sqrt{x}-2}{x-\sqrt{x}-2}\right)\)

\(P=\frac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}\cdot\left(\frac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\frac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\right)\)

\(P=\left(\sqrt{x}-1\right)\cdot\left(\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}\right)\)

\(P=\left(\sqrt{x}-1\right)\cdot\left(\frac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)=\left(\sqrt{x}-1\right)\cdot\frac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{2}{\sqrt{x}+1}\)

\(P=\frac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}.\left(\frac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\frac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\right)\)

\(P=\left(\sqrt{x}-1\right).\left(\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}+1}\right)\)

\(P=\left(\sqrt{x}-1\right).\left(\frac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)

\(P=\left(\sqrt{x}-1\right).\frac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(P=\frac{2}{\sqrt{x}+1}\)

\(E=\frac{\sqrt{15}-\sqrt{12}}{\sqrt{5}-2}-\frac{1}{2-\sqrt{3}}=\frac{\sqrt{3}\left(\sqrt{5}-2\right)}{\sqrt{5}-2}-\frac{1}{2-\sqrt{3}}\)

\(=\sqrt{3}-\frac{2+\sqrt{3}}{4-3}=\sqrt{3}-2-\sqrt{3}=-2< 5^{\sqrt{74}}\)

hay Vậy \(E< G\)

n=1 nha

n = 1   ( dễ thế )

ĐK: \(x\ne-1;y\ne-1\)

Ta có: \(x=\frac{1}{2+\sqrt{3}}=\frac{2-\sqrt{3}}{4-3}=2-\sqrt{3}\left(tm\right)\)

          \(y=\frac{1}{2-\sqrt{3}}=\frac{2+\sqrt{3}}{4-3}=2+\sqrt{3}\left(tm\right)\)

Thay  \(x=2-\sqrt{3};y=2+\sqrt{3}\) vào biểu thức ta có:

\(\frac{1}{2-\sqrt{3}+1}+\frac{1}{2+\sqrt{3}+1}=\frac{1}{3-\sqrt{3}}+\frac{1}{3+\sqrt{3}}=\frac{3+\sqrt{3}+3-\sqrt{3}}{9-3}=\frac{6}{6}=1\)

Vậy ....

\(\frac{1}{x+1}+\frac{1}{y+1}=\frac{1}{\frac{1}{2+\sqrt{3}}+1}+\frac{1}{\frac{1}{2-\sqrt{3}}+1}\)

\(=\frac{1}{\frac{1+2+\sqrt{3}}{2+\sqrt{3}}}+\frac{1}{\frac{1+2-\sqrt{3}}{2-\sqrt{3}}}\)

\(=\frac{2+\sqrt{3}}{3+\sqrt{3}}+\frac{2-\sqrt{3}}{3-\sqrt{3}}\)

\(=\frac{\left(2+\sqrt{3}\right)\left(\sqrt{3}-1\right)+\left(2-\sqrt{3}\right)\left(\sqrt{3}+1\right)}{\sqrt{3}\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}\)

\(=\frac{2\sqrt{3}}{2\sqrt{3}}=1\)

Ta có : \(n^2-6n+5=\left(n-5\right)\left(n-1\right)\)(*) 

Để (*) là số nguyên tố khi \(n-5=1\)và \(n-1\)là số nguyên tố 

\(\Leftrightarrow n=6\left(tm\right)\)

Vậy n = 6 thì (*) là số nguyên tố