4513 x5421646545644592156495216562=
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bất đẳng thức cần chứng minh viết lại thành:
\(\frac{\left(a+b\right)^3}{\left(b+c\right)^3}+\frac{\left(a+c\right)^3}{\left(b+c\right)^3}+\frac{3\left(a+b\right)\left(a+c\right)\left(b+c\right)}{\left(b+c\right)^3}\le5\)
Đặt: \(x=\frac{a+b}{b+c};y=\frac{a+c}{b+c}\), bất đẳng thức chứng minh trở thành:
\(x^3+y^3+3xy\le5\)
Ta có:
\(xy=\frac{a+b}{b+c}+\frac{a+c}{b+c}=\frac{\left(a+b\right)\left(a+c\right)}{\left(b+c\right)^2}\)
\(=\frac{a\left(a+b+c\right)+bc}{\left(b+c\right)^2}=\frac{2a\left(a+b+c\right)-2bc}{\left(b+c\right)^2}\)
Vậy ta được: \(xy+1=\frac{\left(a+b\right)^2+\left(a+c\right)^2}{\left(b+c\right)^2}=x^2+y^2\)
\(x^3+y^3=x+y\)nên \(x^3+y^3+3xy\le5\Leftrightarrow x+y+3xy\le5\)
Mà ta có: \(\left(x+y\right)^2\le2\left(x^2+y^2\right)=\frac{xy+1}{2}\le\frac{1}{2}+\frac{\left(x+y\right)^2}{8}\)
\(\Rightarrow x+y\le2\Rightarrow xy\le1\)
Do đó ta được: \(x+y+3xy\le5\). Vậy bài toán đã được chứng minh.

- Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện và sinα = a thì ta viết α = arcsin a.
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
- Phương trình sinx = a (1)
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện 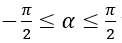
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π - arcsina + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình cosx = a (2)
♦ |a| > 1: phương trình (2) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.
Khi đó phương trình (2) có các nghiệm là
x = α + k2π, k ∈ Z
và x = -α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện 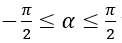
Khi đó các nghiệm của phương trình (2) là
x = arccosa + k2π, k ∈ Z
và x = -arccosa + k2π, k ∈ Z.
Các trường hợp đặc biệt:
- Phương trình tanx = a (3)
Điều kiện:
Nếu α thỏa mãn điều kiện 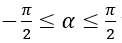
Khi đó các nghiệm của phương trình (3) là
x = arctana + kπ,k ∈ Z
- Phương trình cotx = a (4)
Điều kiện: x ≠ kπ, k ∈ Z.
Nếu α thỏa mãn điều kiện 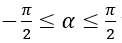
Khi đó các nghiệm của phương trình (4) là
x = arccota + kπ, k ∈ Z

Bất đẳng thức cần chứng minh tương đương với:
\(\dfrac{a}{a+3\sqrt{bc}}+\dfrac{b}{b+3\sqrt{ca}}+\dfrac{c}{c+3\sqrt{ab}}\)
Ta áp dụng bất đẳng thức Cô si dạng \(2\sqrt{xy}\le x+y\) cho các căn thức ở mẫu, khi đó ta được:
\(\dfrac{a}{a+3\sqrt{bc}}+\dfrac{b}{b+3\sqrt{ca}}+\dfrac{c}{c+3\sqrt{ab}}\ge\) với biểu thức
\(\dfrac{2a}{2a+3b+3c}+\dfrac{2b}{3a+2b+3c}+\dfrac{2c}{3a+3b+2c}\)
Khi đó ta cần chứng minh:
\(\dfrac{2a}{2a+3b+3c}+\dfrac{2b}{3a+2b+3c}+\dfrac{2c}{3a+3b+2c}\ge\dfrac{3}{4}\)
Đặt: \(\left\{{}\begin{matrix}x=2a+3b+3c\\y=3a+2b+3c\\z=3a+3b+2c\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2a=\dfrac{1}{4}\left(3y+3z-5x\right)\\2b=\dfrac{1}{4}\left(3z+3x-5y\right)\\2c=\dfrac{1}{4}\left(3x+3y-5z\right)\end{matrix}\right.\)
Khi đó đẳng thức trên được viết lại thành:
\(\dfrac{3y+3z-5x}{4x}+\dfrac{3z+3x-5y}{4y}+\dfrac{3x+3y-5z}{4z}\ge\dfrac{3}{4}\)
Hay: \(3\left(\dfrac{x}{y}+\dfrac{y}{x}+\dfrac{y}{z}+\dfrac{z}{y}+\dfrac{x}{z}+\dfrac{z}{x}\right)-15\ge3\)
Bất đẳng thức cuối cùng luôn đúng theo bất đẳng thức Cô si.
Vậy bất đẳng thức được chứng minh. Đẳng thức xảy ra khi và chỉ khi \(a=b=c\)
Đặt \(x=\sqrt{a};y=\sqrt{b};z=\sqrt{c}\)
Khi đó bđt đã tro chở thành:
\(\dfrac{yz}{x^2+3yz}+\dfrac{zx}{y^2+3zx}+\dfrac{xy}{z^2+3xy}\le\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{3}-\dfrac{yz}{x^2+3yz}+\dfrac{1}{3}-\dfrac{zx}{y^2+3zx}+\dfrac{1}{3}-\dfrac{xy}{z^2+3xy}\ge1-\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{x^2}{x^2+3yz}+\dfrac{y^2}{y^2+3zx}+\dfrac{z^2}{z^2+3xy}\ge\dfrac{3}{4}\) (đpcm)

`Answer:`
`1.`
Xét `f(x)=0`
`<=>(x+3)(x^2+5x-6)=0`
`<=>x+3=0` hoặc `x^2+5x-6=0`
`<=>x=-3` hoặc `(x-1)(x+6)=0`
`<=>x=-3` hoặc `x=1` hoặc `x=-6`
`f(x)=(x+3)(x-1)(x+6)`

Vậy ta có:
`f(x)>0<=>x\in(-6;-3)∪(1;+oo)`
`f(x)<0<=>x\in(-oo;-6)∪(-3;1)`
`f(x)=0<=>x\in{-6;-3;1}`
`2.`

`=>S=(-2;-6)∪[-2;1)∪(1;3]`


Sử dụng bất đẳng thức Bunhiacopxki dạng phân thức, chú ý đến dấu đẳng thức xẩy ra thì ta được:
\(\frac{1}{a^2+b^2+c^2}+\frac{1}{3ab}+\frac{1}{3bc}+\frac{1}{3ca}\)sẽ lớn hơn hoặc bằng:
\(\frac{16}{a^2+b^2+c^2+3\left(ab+bc+ca\right)}\ge\frac{16}{\left(a+b+c\right)^2}+\frac{1}{3}\left(a+b+c\right)^2=12\)
\(\Rightarrow\)Ta cần chứng minh: \(\frac{2}{3}\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)\ge18\)
Để ý tiếp bất đẳng thức Bunhiacopxki ta được:
\(\frac{2}{3}\left(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\right)\ge\frac{6}{ab+bc+ca}\ge\frac{6}{\frac{1}{3}\left(a+b+c\right)^2}=18\)
Do đó ta có bất đẳng thức:
\(\frac{1}{a^2+b^2+c^2}+\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\ge\frac{1}{a^2+b^2+c^2}+\frac{9}{ab+bc+ca}\)
Vậy bất đẳng thức được chứng minh.
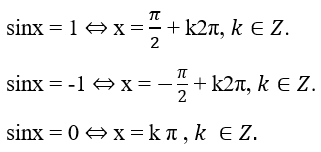
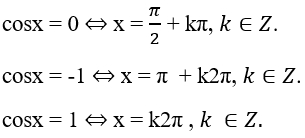
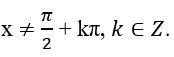
 giúp mình ạ
giúp mình ạ
123dA