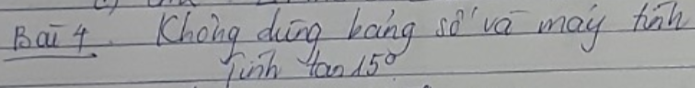
giúp với các bạn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(2^a=x;2^b=y;2^c=z\)
\(\Rightarrow\hept{\begin{cases}8^a=x^3;8^b=y^3;8^c=z^3\\xyz=2^{a+b+c}=1\end{cases}}\)
Ta có: \(x^3+1+1\ge3\sqrt[3]{1.1.x^3}=3x\)
CMTT \(y^3+1+1\ge3y\);\(z^3+1+1\ge3z\)
\(\Rightarrow x^3+y^3+z^3\ge3\left(x+y+z-2\right)\)
\(\ge x+y+z+2\left(x+y+z-3\right)\)
\(\ge x+y+z+2\left(3\sqrt[3]{xyz}-3\right)\)
\(\ge x+y+z\)( vì xyz =1)
=> đpcm

Gọi số học sinh lúc đầu của nhóm đó là \(x\)(học sinh) \(x\inℕ^∗\).
Mỗi bạn lúc đầu trồng số cây là: \(\frac{120}{x}\)(cây)
Số học sinh lúc sau là: \(x+3\)(học sinh)
Mỗi bạn trồng số cây là: \(\frac{120}{x}-2\)(cây).
Ta có phương trình: \(\left(x+3\right)\left(\frac{120}{x}-2\right)=120\)
\(\Rightarrow120x+360-2x^2-6x=120x\)
\(\Leftrightarrow-2x^2-6x+360=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=12\left(tm\right)\\x=-15\left(l\right)\end{cases}}\)

xét bđt sau \(\left(\sqrt{a}+\sqrt{b}\right)^2=a+b+2\sqrt{ab}\ge\left(\sqrt{a+b}\right)^2\)
\(2\sqrt{ab}\ge0\)( luôn đúng)
\(\sqrt{a}+\sqrt{b}\ge\sqrt{a+b}\)
\(a,A=\sqrt{x-2}+\sqrt{6-x}\)
\(A=\sqrt{x-2}+\sqrt{6-x}\ge\sqrt{x-2+6-x}=\sqrt{4}=2\)
dấu "=" xảy ra khi và chỉ khi \(\orbr{\begin{cases}x=2\\x=6\end{cases}}\)
\(< =>MIN:A=2\)
áp dụng bđt bunhia cốp - xki với bộ số \(\left(\sqrt{x-2};\sqrt{6-x}\right);\left(1;1\right)\)
\(A^2=\left(\sqrt{x-2}+\sqrt{6-x}\right)^2\le\left(1^2+1^2\right)\left(x-2+6-x\right)\)
\(A^2\le2.4\)
\(A\le2\sqrt{2}\)
dấu "=" xảy ra khi và chỉ khi \(\frac{\sqrt{x-2}}{1}=\frac{\sqrt{6-x}}{1}\)
\(\sqrt{x-2}=\sqrt{6-x}\)
\(x=4\)
\(MAX:A=2\sqrt{2}\)

Đk: x \(\ge\)0 và x \(\ne\)1
Ta có: \(P=\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{3}{\sqrt{x}+1}-\frac{6\sqrt{x}-4}{x-1}\)
\(P=\frac{\sqrt{x}\left(\sqrt{x}+1\right)+3\left(\sqrt{x}-1\right)-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(P=\frac{x+\sqrt{x}+3\sqrt{x}-3-6\sqrt{x}+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(P=\frac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}-1}{\sqrt{x}+1}\)
b) Với x \(\ge\)0 và x \(\ne\)1 (2)
Ta có: \(P< \frac{1}{2}\) <=> \(\frac{\sqrt{x}-1}{\sqrt{x}+1}< \frac{1}{2}\) <=> \(2\sqrt{x}-2< \sqrt{x}+1\)
<=> \(\sqrt{x}< 3\) <=> x < 9 (1)
Từ (1) và (2) => \(0\le x< 9\) và x \(\ne\)1

Đk: x \(\ge\)0 và x \(\ne\)1
a)\(P=\frac{3\left(x+\sqrt{x}-3\right)}{x+\sqrt{x}-2}+\frac{\sqrt{x}+3}{\sqrt{x}+2}-\frac{\sqrt{x}-2}{\sqrt{x}-1}\)
\(P=\frac{3x+3\sqrt{x}-9+\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\frac{3x+3\sqrt{x}-9+x+2\sqrt{x}-3-x+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\frac{3x+5\sqrt{x}-8}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\frac{3x+8\sqrt{x}-3\sqrt{x}-8}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)
\(P=\frac{\left(3\sqrt{x}+8\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}=\frac{3\sqrt{x}+8}{\sqrt{x}+2}\)
b) Với x \(\ge\)0 và x \(\ne\)1 (1), ta có:
\(P< \frac{15}{4}\) <=> \(\frac{3\sqrt{x}+8}{\sqrt{x}+2}< \frac{15}{4}\) <=> \(12\sqrt{x}+32< 15\sqrt{x}+30\)
<=> \(3\sqrt{x}>2\) <=> \(\sqrt{x}>\frac{2}{3}\) <=> \(x>\frac{4}{9}\)(2)
Từ (1) và (2) => \(x>\frac{4}{9}\) và x \(\ne\)1

\(A=\frac{\sqrt{x}}{\sqrt{x}+3}+\frac{2\sqrt{x}}{\sqrt{x}-3}-\frac{3x+9}{x-9}\)
\(A=\frac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(A=\frac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(A=\frac{3\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\frac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\frac{3}{\sqrt{x}+3}\)
b) Với x \(\ge\)0; x khác 9
Ta có: \(A=\frac{1}{3}\) <=> \(\frac{3}{\sqrt{x}+3}=\frac{1}{3}\) <=> \(\sqrt{x}+3=9\) <=> \(\sqrt{x}=6\) <=> x= 36 (tm)
c) Ta có: \(\sqrt{x}+3\ge3\) => \(\frac{3}{\sqrt{x}+3}\le\frac{3}{3}=1\) => A \(\le\)1
Dấu "=" xảy ra<=> x = 0
Vậy MaxA = 1 <=> x = 0

Ta có: \(\frac{1}{\left(n+1\right)\sqrt{n}+n.\sqrt{n+1}}=\frac{1}{\sqrt{n.\left(n+1\right)}.\left(\sqrt{n+1}+\sqrt{n}\right)}\)
\(=\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n.\left(n+1\right)}.\left(n+1-n\right)}\)
\(=\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n.\left(n+1\right)}}\)
\(=\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\)
\(T=\frac{1}{2\sqrt{1}+1\sqrt{2}}+\frac{1}{3\sqrt{2}+2\sqrt{3}}+...+\frac{1}{100\sqrt{99}+99\sqrt{100}}\)
\(=\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{99}}-\frac{1}{\sqrt{100}}\)
\(=1-\frac{1}{\sqrt{100}}=\frac{9}{10}\)
b) \(\Leftrightarrow1-\frac{1}{\sqrt{n+1}}=\frac{4}{5}\)( làm tắt nhé )
\(\Leftrightarrow\frac{1}{\sqrt{n+1}}=\frac{1}{5}\)
\(\Leftrightarrow\sqrt{n+1}=5\)
\(\Leftrightarrow n=24\)
Vậy ...

\(A=\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\frac{1}{\sqrt{5}+\sqrt{6}}+...+\frac{1}{\sqrt{79}+\sqrt{80}}\)
\(2A=\frac{2}{\sqrt{1}+\sqrt{2}}+\frac{2}{\sqrt{3}+\sqrt{4}}+\frac{2}{\sqrt{5}+\sqrt{6}}+...+\frac{2}{\sqrt{79}+\sqrt{80}}\)
\(>\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\frac{1}{\sqrt{4}+\sqrt{5}}+...+\frac{1}{\sqrt{79}+\sqrt{80}}+\frac{1}{\sqrt{80}+\sqrt{81}}\)
\(=\frac{\sqrt{2}-1}{2-1}+\frac{\sqrt{3}-\sqrt{2}}{3-2}+\frac{\sqrt{4}-\sqrt{3}}{4-3}+...+\frac{\sqrt{81}-\sqrt{80}}{81-80}\)
\(=\sqrt{2}-1+\sqrt{3}-\sqrt{2}+\sqrt{4}-\sqrt{3}+...+\sqrt{81}-\sqrt{80}\)
\(=\sqrt{81}-1=8\)
suy ra đpcm.
\(\tan15^o=\tan\left(45^o-30^o\right)\)
\(=\frac{\tan45^o-\tan30^o}{1+\tan45^o.\tan30^o}\)
\(=\frac{1-\frac{\sqrt{3}}{3}}{1+1.\frac{\sqrt{3}}{3}}\)
\(=\frac{1-\frac{\sqrt{3}}{3}}{1+\frac{\sqrt{3}}{3}}\)