Chứng tỏ rằng với mọi số tự nhiên n thì : (n + 20182019) (n + 20192018) chia hết cho 2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A
1

28 tháng 12 2020
Gọi \(3n+2;5n+3=d\left(d\inℕ^∗\right)\)
\(3n+2⋮d\Rightarrow15n+10⋮d\)
\(5n+3⋮d\Rightarrow15n+9⋮d\)
Suy ra : \(15n+10-15n-9⋮d\)
\(1⋮d\)hay \(d\in\left\{1\right\}\)
Tương tự mấy phần kia :D
LT
0

DT
0

HM
2

26 tháng 12 2020
tớ giải cho xem này
x+5+7+9+...+45+47+49=640
x+(5+7+9...+45+47+49)=640
Từ 5 đến 49 có số số hạng là:
(49-5):(7-5)+1=23 (số)
Tổng các số từ 5 đến 49 là:
(49+5).23:2=621
=>x=640-621
=>x=19
Vậy x =19
DT
2

25 tháng 12 2020
(x-y)(y-1)+y=15
xy-y^2+y-x+y=15
(xy-x)-(y^2-2y+1)=14
x(y-1)-(y-1)^2=14
(y-1)(x-y+1)=14
=>y-1; x-y+1 thuộc Ư(14)
đến đây bn tụ tính ra nha
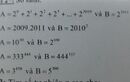
- Nếu \(n⋮2\) thì \(\left(n+2018^{2019}\right)⋮2\) ( vì \(n⋮2;2018^{2019}⋮2\) )
\(\Rightarrow\left(n+2018^{2019}\right)\left(n+2019^{2018}\right)⋮2\)
- Nếu n không chia hết cho 2
\(\Rightarrow n:2\) dư 1
\(\Rightarrow n=2k+1\left(k\inℕ\right)\)
\(\Rightarrow n+2019^{2018}=2k+1+2019^{2018}⋮2\)
\(\Rightarrow\left(n+2018^{2019}\right)\left(n+2019^{2018}\right)⋮2\)
Vậy với mọi \(n\inℕ\) thì \(\left(n+2018^{2019}\right)\left(n+2019^{2018}\right)⋮2\)
* Nếu n là lẻ
(n+2018\(^{2019}\))(n+2019\(^{2018}\)), vì 2018\(^{2019}\)là chẵn nên n+2018\(^{2019}\)là lẻ, vì 2019\(^{2018}\)là lẻ , nên n+2019\(^{2018}\)là chẵn.
=>(n+2018\(^{2019}\))(n+2019\(^{2018}\)) là chẵn nên chia hết cho 2 (1)
* Nếu n là chẵn
(n+2018\(^{2019}\))(n+2019\(^{2018}\)), vì 2018\(^{2019}\)là chẵn nên n+2018\(^{2019}\)là chẵn, vì 2019\(^{2018}\)là lẻ , nên n+2019\(^{2018}\)là lẻ.
=>(n+2018\(^{2019}\))(n+2019\(^{2018}\)) là chẵn nên chia hết cho 2 (2)
Từ (1) và (2) => với mọi số tự nhiên n thì (n+2018\(^{2019}\))(n+2019\(^{2018}\)) chia hết cho 2
chúc học tốt