Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Mệnh đề phủ định của mệnh đề P: "2≤2" là
Câu nào sau đây không phải là mệnh đề?
Hình vẽ nào sau đây có phần không bị gạch minh họa cho tập hợp (1;4]?




Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn?
Miền nghiệm của bất phương trình 3x+2(y+3)≥4(x+1)−y+3 là nửa mặt phẳng chứa điểm nào sau đây?
Giá trị của biểu thức A=sin215∘+sin275∘+cos120∘ là
Cho tam giác ABC có AB=5, AC=2, C=45∘. Độ dài cạnh BC là
Mệnh đề phủ định của "20 là số hợp số" là
Cho A=[1;4];B=(2;6);C=(1;2). Tập A∩B∩C là
Cho A là tập hợp các số tự nhiên chẵn không lớn hơn 10, B={n∈Nn≤6}, C={n∈N4≤n≤10}. Tập hợp A∩(B∪C) là
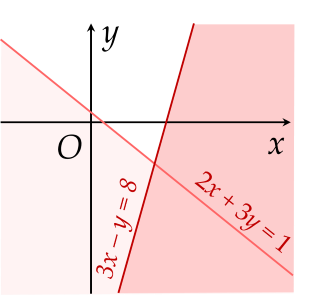
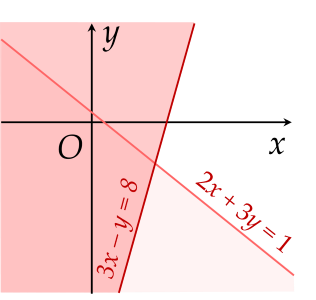
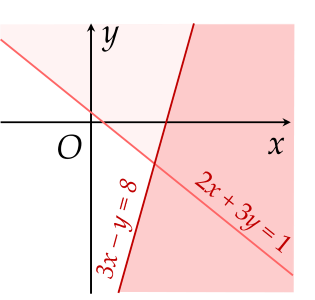
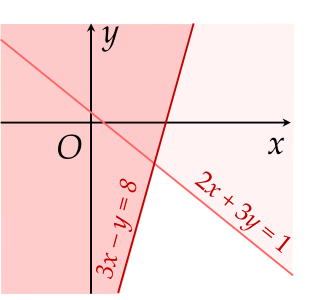
Miền nghiệm của hệ bất phương trình {2x+3y≤13x−y≥8 là phần không tô màu (có tính cả biên) của hình vẽ nào trong các hình vẽ sau?
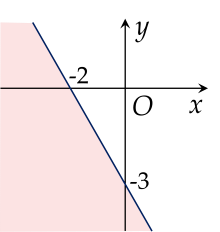
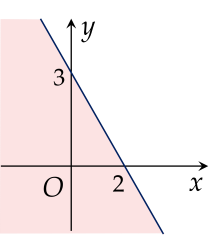
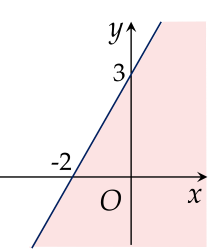
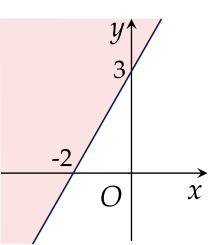
Miền nghiệm của bất phương trình 3x−2y>−6 là phần tô màu (không kể đường thẳng) trong hình vẽ nào sau đây?
Cho A là tập hợp các học sinh lớp 10 đang học ở trường X và B là tập hợp các học sinh đang học môn Tiếng Anh của trường X.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) A∩B là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường X. |
|
| b) A\B là tập hợp những học sinh lớp 10 và không học Tiếng Anh ở trường X. |
|
| c) A∪B là tập hợp các học sinh lớp 10 và học sinh học môn Tiếng Anh ở trường X. |
|
| d) B\A là tập hợp các học sinh học lớp 10 ở trường X nhưng không học môn Tiếng Anh. |
|
Đô thích ăn hai loại trái cây là cam và xoài, mỗi tuần mẹ cho Đô 200 nghìn đồng để mua trái cây. Biết rằng giá cam là 15 000 đồng/1 kg, giá xoài là 30 000 đồng/1 kg. Gọi x,y (với a>0;y>0) lần lượt là số ki-lô-gam cam và xoài mà Đô có thể mua về sử dụng trong một tuần.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Trong tuần, số tiền Đô có thể mua cam là 15000x đồng, số tiền An có thể mua xoài là 30000y đồng. |
|
| b) 3x+6y≥40. |
|
| c) Đô không thể mua đủ 5 kg cam, 4 kg xoài sử dụng trong tuần. |
|
| d) Đô có thể mua 4 kg cam, 6 kg xoài sử dụng trong tuần. |
|
Cho cosα=−43 với 0∘<α<90∘.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) sin2α=167. |
|
| b) sinα<0. |
|
| c) sinα=−47. |
|
| d) cotα=−737. |
|
Một trò chơi chọn ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ A thì người ấy được cộng 3 điểm, nếu người chơi chọn được chữ B thì người ấy bị trừ 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20. Gọi x,y theo thứ tự là số lần người chơi chọn được chữ A và chữ B.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Tổng số điểm người chơi đạt được khi chọn chữ A là 3x, tổng số điểm người chơi bị trừ khi chọn chữ B là y. |
|
| b) Bất phương trình bậc nhất hai ẩn x,y trong tình huống người chơi chiến thắng là 3x−y≤20. |
|
| c) Người chơi chọn được chữ A 7 lần và chọn được chữ B 1 lần thì người đó vừa đủ điểm giành chiến thắng trò chơi. |
|
| d) Người chơi chọn được chữ A 8 lần và chọn được chữ B 3 lần thì người đó vừa đủ điểm giành chiến thắng trò chơi. |
|
Cho hai tập hợp khác rỗng A=(m−3;5], B=(−2;3m+1) với m∈R. Tìm số nguyên m lớn nhất để A⊂B.
Trả lời:
Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lí, 14 học sinh giỏi cả môn Toán và Lí và có 6 học sinh không giỏi môn nào cả. Lớp học đó có bao nhiêu học sinh?
Trả lời:
Cho tam giác ABC có A(0;3);B(−1;2);C(2;1). Có bao nhiêu giá trị nguyên của tham số m để điểm M(m;22m−1) nằm bên trong tam giác ABC?
Trả lời:
Một công ty X có hai phân xưởng A,B cùng sản xuất hai loại sản phẩm M,N. Số đơn vị sản phẩm các loại được sản xuất ra và chi phí mỗi giờ hoạt động của A,B như sau:
| Phân xưởng A | Phân xưởng B | |
| Sản phẩm M | 250 | 250 |
| Sản phẩm N | 100 | 200 |
| Chi phí | 600 000 | 1 000 000 |
Công ty nhận được yêu cầu đặt hàng là 5 000 đơn vị sản phẩm M và 3 000 đơn vị sản phẩm N. Công ty đã tìm được cách phân phối thời gian cho mỗi phân xưởng hoạt động thỏa mãn yêu cầu đơn đặt hàng và chi phí thấp nhất. Chi phí thấp nhất bằng bao nhiêu triệu đồng?
Trả lời:
Biết miền nghiệm của hệ bất phương trình ⎩⎨⎧2x+2y≤102y≤42x+4y≤12x≥0y≥0 là một đa giác. Tính diện tích của đa giác đó (làm tròn kết quả tới hàng phần mười).
Trả lời:
Gọi Slà diện tích một cánh buồm hình tam giác. Biết cánh buồm đó có chiều dài một cạnh là 3,2 m và hai góc kề cạnh đó có số đo là 48∘ và 105∘. Tính S. (Làm tròn kết quả đến chữ số thập phân thứ nhất của đơn vị m2)
Trả lời:

