Đề ôn tập và kiểm tra giữa học kì I toán 12 cấu trúc mới mới nhất

Câu 1 (1đ):

Cho hàm số $y=\dfrac{2x-3}{4-x}$ . Khẳng định nào sau đây đúng?

Hàm số nghịch biến trên

\mathbb{R}

.

Hàm số nghịch biến trên mỗi khoảng xác định.

Hàm số đồng biến trên

\mathbb{R}

.

Hàm số đồng biến trên mỗi khoảng xác định.

Câu 2 (1đ):

Cho đồ thị $(C)$ của hàm số $y=-x^3+3x^2-5x+2$ . Trong các mệnh đề sau, mệnh đề nào đúng?

(C)

không có điểm cực trị.

(C)

có hai điểm cực trị.

(C)

có một điểm cực trị.

(C)

có ba điểm cực trị.

Câu 3 (1đ):

Cho hàm số $y=f(x)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên sau:

Khẳng định nào sau đây đúng?

Giá trị nhỏ nhất của hàm số bằng

-1.

Giá trị lớn nhất của hàm số bằng

2

.

Giá trị nhỏ nhất của hàm số bằng

-1

và

1

.

Giá trị nhỏ nhất của hàm số bằng

1

.

Câu 4 (1đ):

Đường thẳng $y=ax+b$ với $a, \, b \in \mathbb{R}$ và $a\ne 0$ là tiệm cận xiên của đồ thị hàm số $y=f(x)$ . Mệnh đề nào sau đây đúng?

\underset{x\to +\infty }{\mathop{\lim }}\,\big[f(x )-(ax+b)\big]=0

hoặc

\underset{x\to -\infty }{\mathop{\lim }}\,\big[f(x )-(ax+b)\big]=0

.

\underset{x\to +\infty }{\mathop{\lim }}\,\big[f(x )-(ax+b)\big]=a

.

\underset{x\to +\infty }{\mathop{\lim }}\,\big[f(x )-(ax+b)\big]=b

.

\underset{x\to +\infty }{\mathop{\lim }}\,\big[f'(x)-(ax+b)\big]=0

.

Câu 5 (1đ):

Đồ thị hàm số $y=3x^2+x+2$ và trục tung có bao nhiêu điểm chung?

1

.

3

.

0

.

2

.

Câu 6 (1đ):

Giá trị của $a,\,b$ để hàm số $y=\dfrac{ax+b}{x+1}$ có đồ thị như hình vẽ dưới là

a=1,\,b=-2

.

a=-1,\,b=-2

.

a=2,\,b=1

.

a=-2,\,b=1

.

Câu 7 (1đ):

Cho tứ diện $ABCD$ . Gọi $G$ là trọng tâm tam giác $ABC.$ Giá trị của $k$ thích hợp điền vào đẳng thức vectơ $\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=k\overrightarrow{DG}$ là

k=\dfrac{1}{3}

.

k=\dfrac{1}{2}

.

k=2.

k=3.

Câu 8 (1đ):

Trong không gian với hệ tọa độ $Oxyz$ , cho ba điểm $A(1;\,-1;\,1)$ , $B( 3;\,2;\,-2)$ , $C( -3;\,1;\,5)$ . Tọa độ điểm $D$ thỏa mãn $\overrightarrow{AB}=\overrightarrow{CD}$ là

D( -1;\,4;\,2)

.

D( 1;\,4;\,2)

.

D( -1;-\,4;\,2)

.

D( 1;-\,4;-\,2)

.

Câu 9 (1đ):

Trong không gian $O x y z$ , cho vectơ $\overrightarrow{a}=2 \overrightarrow{i}+\overrightarrow{j}-2 \overrightarrow{k}$ . Độ dài của vectơ $\overrightarrow{a}$ bằng

4 .

1 .

5 .

3.

Câu 10 (1đ):

Cho hàm số $y=\dfrac{\sin x+1}{{{\sin }^{2}}x+\sin x+1}$ . Gọi $M$ là giá trị lớn nhất và $m$ là giá trị nhỏ nhất của hàm số đã cho. Giá trị của $M - m$ là

1

.

0

.

-1

.

\dfrac32

.

Câu 11 (1đ):

Cho hàm số $y=\dfrac{2x-1}{x+3}$ . Diện tích hình giới hạn bởi $2$ trục tọa độ và đường tiệm cận của đồ thị hàm số đã cho là

S=3

.

S=6

.

S=\sqrt{13}

.

S=5

.

Câu 12 (1đ):

Giá trị lớn nhất của hàm số $y={{x}^{4}}-2{{x}^{2}}+3$ trên đoạn $\left[ 0;\sqrt{3} \right]$ là

M=6

.

M=9

.

M=8\sqrt{3}

.

M=1

.

Câu 13 (1đ):

Cho hàm số $y=f(x)$ liên tục và có đồ thị trên đoạn $[-2 ; 4]$ như hình vẽ.

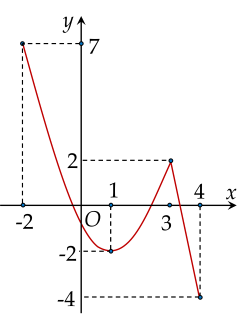
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Trên đoạn $[-2 ; 4]$ , đồ thị hàm số $y = f(x)$ có $2$ điểm cực trị.
b) Giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;2]$ là $-2$ .
c) Giá trị lớn nhất của hàm số $y = f(x)$ trên đoạn $[1;4]$ là $-4$ .
d) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $[-2;4]$ là $11$ .

Câu 14 (1đ):

Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:

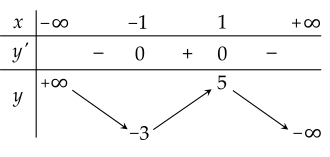
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Phương trình $2f(x)=5$ có $3$ nghiệm.
b) Hàm số đồng biến trên khoảng $(-3 ; 5)$ .
c) Giá trị lớn nhất của hàm số trên $[-1 ; 2]$ bằng $1$ .
d) Hàm số đã cho có $2$ cực trị.

Câu 15 (1đ):

Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong $t$ giờ được cho bởi hàm số có công thức $c(t)=\dfrac{t}{t^2+1}$ (mg/L).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Nồng độ thuốc trong máu của bệnh nhân sau $3$ giờ là $c(3)=\dfrac{3}{10}$ (mg/L).
b) Đạo hàm của hàm số $c(t)=\dfrac{t}{t^2+1}$ là $c'(t)=\dfrac{1-t^2}{(t^2+1)^2}$ .
c) Nồng độ thuốc trong máu bệnh nhân tăng trong khoảng $t\in (0;\,2)$ .
d) Nồng độ thuốc trong máu của bệnh nhân cao nhất khi $t=\dfrac{1}{2}$ .

Câu 16 (1đ):

Một vật nặng $O$ được kéo từ ba hướng như hình vẽ và chịu tác dụng của ba lực $\overrightarrow{F_1},\,\overrightarrow{F_2},\,\overrightarrow{F_3}$ , có độ lớn lần lượt là $24$ N, $12$ N, $6$ N. Biết góc tạo bởi hai lực $\overrightarrow{F_1},\,\overrightarrow{F_2}$ là $120^\circ$ và lực thứ ba vuông góc với hai lực đầu tiên.

loading...

Trong đó điểm $D$ là đỉnh của hình bình hành $OBDA$ và $E$ là đỉnh của hình bình hành $OCED$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{BO}+\overrightarrow{BA}=\overrightarrow{BD}$ .
b) $\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ .
c) Độ dài vectơ $\overrightarrow{OD}$ là $12\sqrt{7}$ .
d) Độ lớn hợp lực tác dụng vào vật $O$ là $6\sqrt{13}$ N.

Câu 17 (1đ):

Ban đầu bạn An ở vị trí điểm $A$ muốn đến điểm $C$ ở bên bờ sông. Biết rằng An đứng đối diện và cách chiếc cọc tại điểm $B$ một khoảng cách $10$ km. Khi sang sông, An sẽ đến vị trí điểm $M$ bất kì thuộc đoạn thẳng $BC$ .

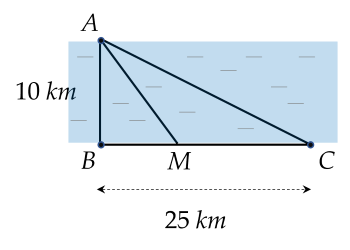
loading...

Biết trên sông, An di chuyển với vận tốc $30$ km/h và trên đất liền, An di chuyển với vận tốc $50$ km/h. Tính $5MB+3MC$ (đơn vị km) để bạn An đến vị trí điểm $C$ nhanh nhất?

Trả lời:

Câu 18 (1đ):

Một xí nghiệp $A$ chuyên cung cấp sản phẩm $S$ cho nhà phân phối $B$ . Hai bên thỏa thuận rằng, nếu đầu tháng $B$ đặt hàng $x$ tạ sản phẩm $S$ thì giá bán mỗi tạ sản phẩm $S$ là $P(x)=6-0,0005x^2$ (triệu đồng) $(x\le 40)$ . Chi phí $A$ phải bỏ ra cho $x$ tạ sản phẩm $S$ trong một tháng là $C(x)=10+3,5x$ (triệu đồng) và mỗi sản phẩm bán ra phải chịu thêm mức thuế là $1$ triệu đồng. Trong một tháng $B$ cần đặt hàng bao nhiêu tạ sản phẩm $S$ thì $A$ có được lợi nhuận lớn nhất, kết quả làm tròn đến hàng phần mười.

Trả lời:

Câu 19 (1đ):

Có ba lực cùng tác động vào một vật. Hai trong ba lực này hợp với nhau một góc $100^\circ$ và có độ lớn lần lượt là $25$ N và $12$ N. Lực thứ ba vuông góc với mặt phẳng tạo bởi hai lực đã cho và có độ lớn $4$ N. Tính độ lớn của hợp lực của ba lực trên. (làm tròn đến hàng đơn vị)

Trả lời:

Câu 20 (1đ):

Người ta muốn làm một cái bể dạng hình hộp chữ nhật không nắp (như hình vẽ) có thể tích bằng $1$ m $^3$ . Chiều cao của bể là $5$ dm, các kích thước khác là $x$ m, $y$ m với $x>0$ và $y>0$ . Diện tích toàn phần của bể (không kể nắp) là hàm số $S(x)$ trên khoảng $\left(0;+\infty \right)$ .

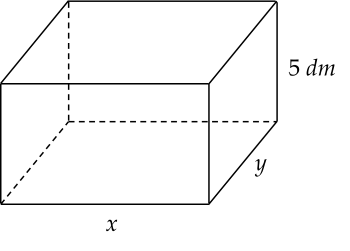
loading...

Đường tiệm cận xiên của đồ thị hàm số $S(x)$ là đường thẳng $y=ax+b$ . Tính $P=a^2+b^2$ .

Trả lời:

Câu 21 (1đ):

Cho hàm số $y = g(x)=ax^4+bx^3+cx^2+dx+e$ có đồ thị như hình vẽ dưới đây.

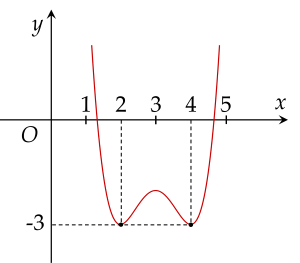
loading...

Hàm số $y = f(x)=g[g(x)]$ có bao nhiêu điểm cực tiểu?

Trả lời:

Câu 22 (1đ):

Có tất cả bao nhiêu giá trị nguyên của tham số $m$ thuộc $[-2 \, 025;2 \, 025]$ để hàm số $y=\ln (x^2+2 \, 024)-mx+2 \, 025$ đồng biến trên $\mathbb{R}$ ?

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 1) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP