Bài học cùng chủ đề
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Đề kiểm tra giữa học kì I (đề số 2) SVIP
Yêu cầu đăng nhập!
Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!
Câu nào sau đây là một mệnh đề?
Cho ba tập hợp A={0;1;2;3;4;5;6;7}, B={0;2;4;6;8}, C={1;3;5;7}. Khẳng định nào sau đây đúng?
Bất phương trình nào sau đây không là bất phương trình bậc nhất hai ẩn?
Điểm A(0;3) không thuộc miền nghiệm của bất phương trình nào sau đây?
Parabol (P):y=3x2−2x+1 có đỉnh là
Giá trị của B=cos273∘+cos287∘+cos23∘+cos217∘ là
Cho tam giác ABC có AB=6, AC=8, A=60∘. Độ dài cạnh BC là
Trong tam giác ABC có B=75∘, C=45∘, AB=6. Độ dài cạnh BC bằng
Trong các câu sau, có bao nhiêu câu là mệnh đề chứa biến và không phải mệnh đề?
i) "2x+1 là số lẻ, (x là số tự nhiên)".
ii) "x+1=0".
iii) "x−2y>0".
iv) "(x+y)2 là số chính phương, (x,y là số tự nhiên khác 0)".
Cho A=[m;m+1]; B=[1;4). Các giá trị của m để A∩B=∅ là
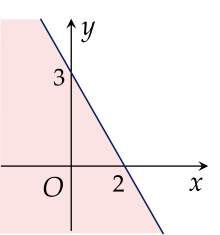
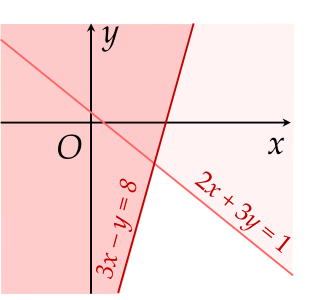
Phần tô màu (không bao gồm đường thẳng) trong hình vẽ là miền nghiệm của bất phương trình nào sau đây?
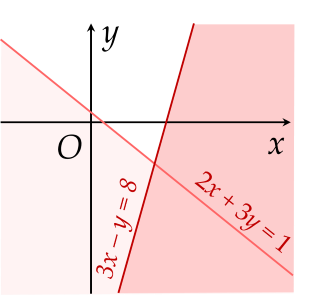
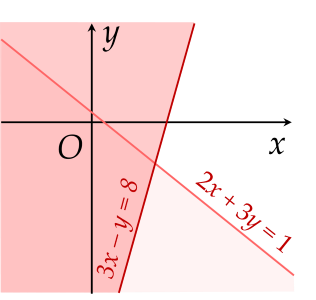
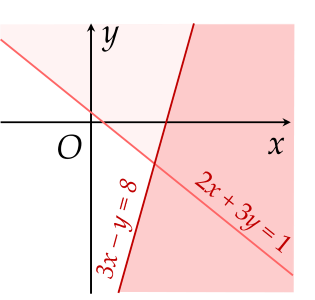
Miền nghiệm của hệ bất phương trình {2x+3y≤13x−y≥8 là phần không tô màu (có tính cả biên) của hình vẽ nào trong các hình vẽ sau?
Cho ba tập hợp CRM=(−∞;3),CRN=(−∞;−3)∪(3;+∞) và CRP=(−2;3].
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) N=(−3;3). |
|
| b) P=(−∞;−2]∪(3;+∞). |
|
| c) M∩N=∅. |
|
| d) (M∩N)∪P=(−∞;−2]∪[3;+∞). |
|
Cho A là tập hợp các học sinh lớp 10 đang học ở trường X và B là tập hợp các học sinh đang học môn Tiếng Anh của trường X.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) A∩B là tập hợp các học sinh lớp 10 học môn Tiếng Anh ở trường X. |
|
| b) A\B là tập hợp những học sinh lớp 10 và không học Tiếng Anh ở trường X. |
|
| c) A∪B là tập hợp các học sinh lớp 10 và học sinh học môn Tiếng Anh ở trường X. |
|
| d) B\A là tập hợp các học sinh học lớp 10 ở trường X nhưng không học môn Tiếng Anh. |
|
Bà Lan được tư vấn bổ sung chế độ ăn kiêng đặc biệt bằng cách sử dụng hai loại thực phẩm khác nhau là X và Y. Mỗi gói thực phẩm X chứa 20 đơn vị canxi, 20 đơn vị sắt và 10 đơn vị vitamin B. Mỗi gói thực phẩm Y chứa 20 đơn vị canxi, 10 đơn vị sắt và 20 đơn vị vitamin B. Yêu cầu hằng ngày tối thiểu trong chế độ ăn uống là 240 đơn vị canxi, 160 đơn vị sắt và 140 đơn vị vitamin B. Mỗi ngày không được dùng quá 12 gói mỗi loại.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hệ bất phương mô tả số gói thực phẩm X và thực phẩm Y mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B là ⎩⎨⎧x+y≥122x+y≥16x+2y≥140≤x≤120≤y≤12. |
|
| b) Điểm (10;8) không thuộc miền nghiệm của hệ bất phương trình mô tả số gói thực phẩm X và thực phẩm Y mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B. |
|
| c) Miền nghiệm của hệ bất phương mô tả số gói thực phẩm X và thực phẩm Y mà bà Lan cần dùng mỗi ngày trong chế độ ăn kiêng để đáp ứng đủ nhu cầu cần thiết đối với canxi, sắt và vitamin B là một ngũ giác. |
|
| d) Biết 1 gói thực phẩm loại X giá 20000 đồng, 1 gói thực phẩm loại Y giá 25 000 đồng. Bà Lan cần dùng 10 gói thực phẩm loại X và 2 gói thực phẩm loại Y để chi phí mua là ít nhất. |
|
Cho sinα=1312, với 0∘<α<90∘.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) cosα<0. |
|
| b) cosα=1−sin2α. |
|
| c) tanα=−512. |
|
| d) cotα=−125. |
|
Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lí, 14 học sinh giỏi cả môn Toán và Lí và có 6 học sinh không giỏi môn nào cả. Lớp học đó có bao nhiêu học sinh?
Trả lời:
Bạn Lan mang theo đúng 15 nghìn đồng để đi mua vở. Vở loại A có giá 3000 đồng một cuốn, vở loại B có giá 4000 đồng một cuốn. Bạn Lan có thể mua nhiều nhất bao nhiêu quyển vở sao cho bạn có cả hai loại vở?
Trả lời:
Trong một cuộc thi pha chế đồ uống gồm hai loại là A và B, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 cốc nước lọc và 210 g đường. Để pha chế một cốc đồ uống loại A cần 1 cốc nước lọc, 30 g đường và 1 g hương liệu. Để pha chế một cốc đồ uống loại B cần 1 cốc nước lọc, 10 g đường và 4 g hương liệu. Mỗi cốc đồ uống loại A nhận được 6 điểm thưởng, mỗi cốc đồ uống loại B nhận được 8 điểm thưởng. Để đạt được số điểm thưởng cao nhất, đội chơi cần pha chế x cốc đồ uống loại A, y cốc đồ uống loại B. Tính x+y.
Trả lời:
Miền nghiệm của hệ ⎩⎨⎧0≤x≤100≤y≤92x+y≥142x+5y≥30 là miền đa giác. Tính diện tích đa giác đó. (làm tròn đến chữ số thập phân thứ nhất)
Trả lời:
Để đo chiều cao của một cột cờ trên đỉnh một toà nhà anh Bắc đã làm như sau: Anh đứng trên một đài quan sát có tầm quan sát cao 5 m so với mặt đất, khi quan sát anh đo được góc quan sát chân cột là 40∘ và góc quan sát đỉnh cột là 50∘, khoảng cách từ chân toà nhà đến vị trí quan sát là 18 m.

Tính tổng chiều cao cột cờ và chiều cao của toà nhà. (Làm tròn kết quả đến chữ số thập phân thứ nhất của đơn vị mét)
Trả lời:
Cho tanα=1. Tính B=2cos2α−sin2αsin2α+1.
Trả lời:
