B=1.44​+4.74​+7.104​+....+94.974​+97.1004​

\(B = 4 \left(\right. \frac{1}{1.4} + \frac{1}{4.7} + \frac{1}{7.10} + . . . . + \frac{1}{94.97} + \frac{1}{97.100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. \frac{3}{1.4} + \frac{3}{4.7} + \frac{3}{7.10} + . . . . + \frac{3}{94.97} + \frac{3}{97.100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. 1 - \frac{1}{4} + \frac{1}{4} - \frac{1}{7} + \frac{1}{7} - \frac{1}{10} + . . . . + \frac{1}{94} - \frac{1}{97} + \frac{1}{97} - \frac{1}{100} \left.\right)\)

\(B = \frac{4}{3} \left(\right. 1 - \frac{1}{100} \left.\right)\)

\(B = \frac{4}{3} . \frac{99}{100}\)

\(B = \frac{33}{25}\).

Vậy \(B = \frac{33}{25}\).

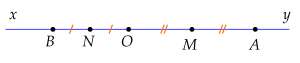
a) Ta có điểm \(M\) nằm giữa \(O\) và \(A\) \(\left(\right. M\) là trung điểm \(O A \left.\right)\) hay \(M\) và \(A\) cùng phía so với \(O\).

Mặt khác \(A\) thuộc tia \(O x\) nên \(M\) thuộc tia \(O x\).

Tương tự, điểm \(N\) nằm giữa \(O\) và \(B\) \(\left(\right. N\) là trung điểm \(O B \left.\right)\) hay \(N\) và \(B\) cùng phía so với \(O\).

Mặt khác \(B\) thuộc tia \(O y\) nên \(N\) thuộc tia \(O y\).

Mà \(O x\) và \(O y\) là hai tia đối nên \(M\) và \(N\) khác phía so với \(O\).

Vậy \(O\) nằm giữa \(M\) và \(N\).

b) Theo đề bài, ta có \(M\) là trung điểm của \(O A\) nên:

\(O M = M A = \frac{O A}{2} = 3\) cm.

Ta có \(N\) là trung điểm của \(O B\) nên:

\(O N = N B = \frac{O B}{2} = \frac{3}{2} = 1 , 5\) cm.

Vì \(O\) nằm giữa điểm \(M\) và \(N\) nên ta có:

\(O M + O N = M N\) hay \(M N = 3 + 1 , 5 = 4 , 5\) cm.

1. Cân nặng của quả dưa hấu là:

\(2 : \frac{2}{3} = 3\) (kg).

Vậy quả dưa hấu nặng \(3\) kg.

2. Số thí sinh Châu Á dự thi là:

\(152. \frac{7}{19} = 56\) (thí sinh)

Số thí sinh Châu Âu, Châu Phi và Châu Mỹ tham gia dự thi là:

\(152 - 56 = 96\) (thí sinh)

Số thí sinh Châu Âu tham gia dự thi là:

\(96. \frac{5}{8} = 60\) (thí sinh)

Số thí sinh Châu Phi và Châu Mỹ dự thi là:

\(96 - 60 = 36\) (thí sinh)

Số thí sinh Châu Mỹ nhiều hơn số thí sinh Châu Phi là \(8\).

Do đó, số thí sinh Châu Mỹ tham gia dự thi là:

\(\left(\right. 36 + 8 \left.\right) : 2 = 22\) (thí sinh)

Số thí sinh Châu Phi dự thi là:

\(22 - 8 = 14\) (thí sinh)

Vậy Châu Á có \(56\) thí sinh, Châu Âu có \(60\) thí sinh, Châu Mỹ có \(22\) thí sinh, Châu Phi có \(14\) thí sinh.

Ta có:

\(A = \frac{1}{1.2} + \frac{1}{3.4} + \frac{1}{5.6} + . . . + \frac{1}{49.50}\)

\(A = \left(\right. 1 + \frac{1}{3} + \frac{1}{5} + . . . + \frac{1}{49} \left.\right) - \left(\right. \frac{1}{2} + \frac{1}{4} + . . . + \frac{1}{50} \left.\right)\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + . . . + \frac{1}{49} + \frac{1}{50} \left.\right) - 2 \left(\right. \frac{1}{2} + \frac{1}{4} + . . . + \frac{1}{50} \left.\right)\)

\(A = \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + . . . + \frac{1}{49} + \frac{1}{50} \left.\right) - \left(\right. 1 + \frac{1}{2} + \frac{1}{3} + . . . + \frac{1}{25} \left.\right)\)

\(A = \frac{1}{26} + \frac{1}{27} + . . . + \frac{1}{49} + \frac{1}{50} < \frac{1}{26} + \frac{1}{26} + \frac{1}{26} + . . . + \frac{1}{26} = \frac{25}{26} < 1.\)

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Âu là:

\(135 , 45 - 88 , 18 = 47 , 27\) (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam năm 2019 với thị trường châu Mỹ là:

\(47 , 27.156 , 32\) (tỉ USD)

Kim ngạch xuất khẩu của Việt Nam với thị trường châu Á lớn hơn tổng kim ngạch xuất khẩu của Việt Nam với thị trường châu Âu và châu Mỹ là:

\(135 , 45 - \left(\right. 47 , 27 + 73 , 89 \left.\right) = 14 , 29\) (tỉ USD).

a)

Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) nên:

\(A C + C B = A B\)

Thay \(A C = 2 , 5\) cm; \(A B = 5\) cm, ta có:

\(2 , 5 + C B = 5\)

\(C B = 5 - 2 , 5\)

\(C B = 2 , 5\) (cm).

b) Vì điểm \(C\) nằm giữa điểm \(A\) và điểm \(B\) và \(A C = C B = 2 , 5\) cm.

Nên điểm \(C\) là trung điểm của đoạn thẳng \(A B\). 

a) Môn Lịch sử và địa lí bạn Minh có ĐTB cao nhất trong học kì I.

b) Môn Toán bạn Minh có tiến bộ nhiều nhất.

c) ĐTB cả năm môn Toán là: \(\frac{7 , 9 + 2.8 , 6}{3} \approx 8 , 4\).

a) \(\frac{3}{4} + \frac{- 1}{3} + \frac{- 5}{18} = \frac{27}{36} + \frac{- 12}{36} + \frac{- 10}{36} = \frac{5}{36}\).

b) \(13 , 57.5 , 5 + 13 , 57.3 , 5 + 13 , 57 = 13 , 57. \left(\right. 5 , 5 + 3 , 5 + 1 \left.\right) = 13 , 57.10 = 135 , 7.\)

1. (Không yêu cầu vẽ hình thật chính xác từng cm).

Do \(A\) là trung điểm \(O B\), nên \(O B = 2. O A\).

Thay số \(O A = 2\) cm, ta có

\(O B = 2.2 = 4\) (cm)

2. (Không yêu cầu vẽ lại hình).

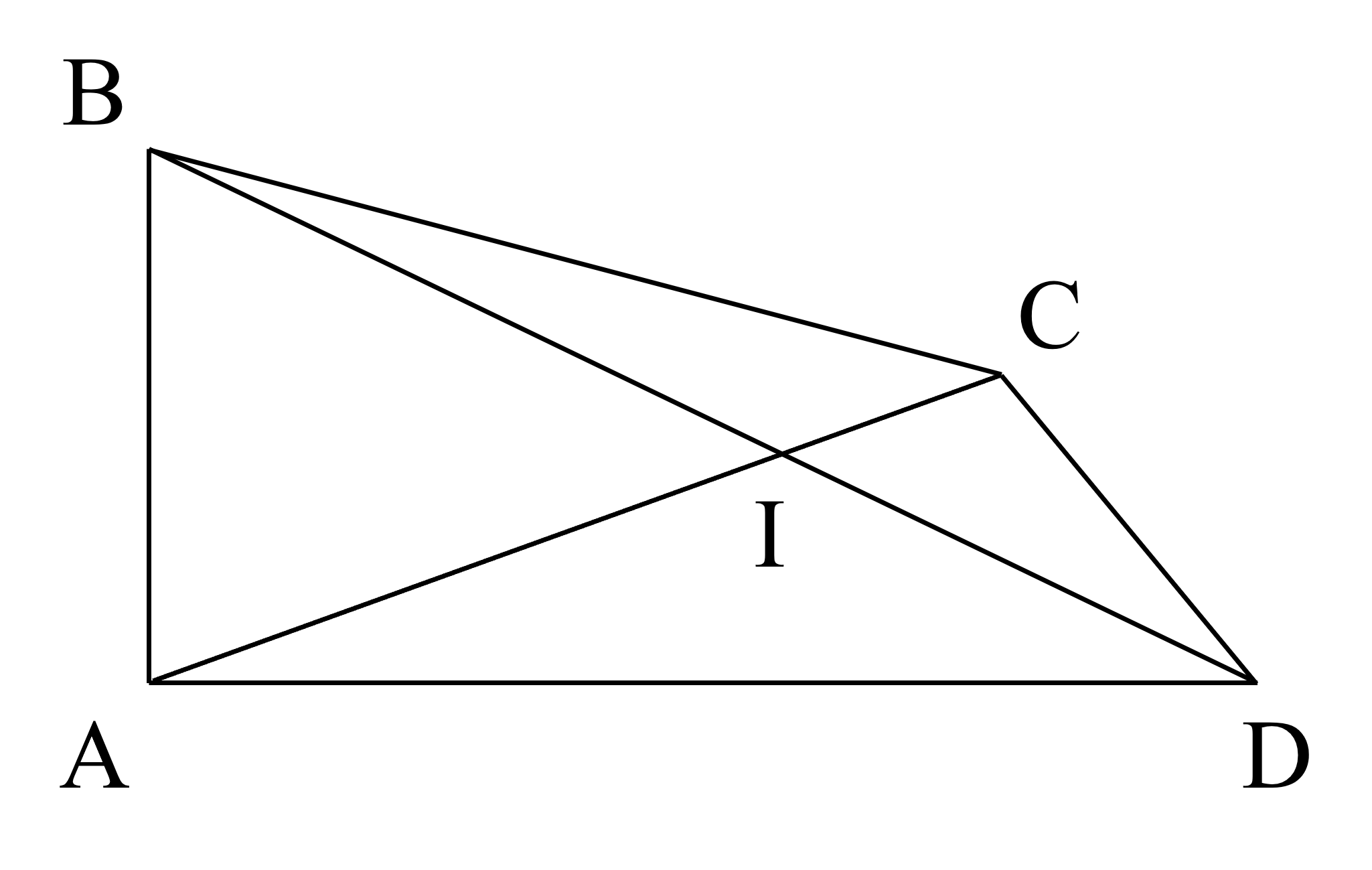
a) Điểm \(C\) và điểm \(I\) nằm trong góc \(B A D\).

b) (Học sinh nêu ra một góc bẹt sẽ đạt điểm tối đa phần này.)

Các góc bẹt trong hình là góc \(B I D\) và \(A I C\).

c) (Không trừ điểm học sinh khi đo góc có sai số từ \(1^{\circ}\) đến \(2^{\circ}\)).

Đo góc, ta lần lượt có các số đo góc như sau:

\(\hat{A I C} = 18 0^{\circ}\)

\(\hat{A C D} = 7 0^{\circ}\)

\(\hat{B C D} = 13 5^{\circ}\)

\(\hat{B A D} = 9 0^{\circ}\)

Sắp xếp các góc theo thứ tự tăng dần về số đo, ta được:

\(\hat{A C D} ; \hat{B A D} ; \hat{B C D} ; \hat{A I C}\).

Số học sinh đạt loại Tốt là:

\(45. \frac{4}{15} = 12\) (học sinh)

Số học sinh đạt loại Khá là:

\(12. \frac{5}{3} = 20\) (học sinh)

Số học sinh được xếp loại Đạt là:

\(45 - 12 - 20 = 13\) (học sinh)

Đáp số: \(13\) học sinh