a, 7x+2=0
7x = 0-2
7x= -2
x= -2/7
b, 18−5x=7+3x.
-5x-3x=7-18
-8x= -11
x= 11/8

Gọi tốc độ của ca nô khi nước yên lặng là \(x\) (km/h) (\(x > 6\) ).

Tốc độ ca nô đi xuôi dòng là \(x + 6\) (km/h)

Ta có \(x \leq 40\) nên \(x + 6 \leq 40 + 6\), tức là \(x + 6 \leq 46\)

Gọi \(s\) (km) là quãng đường ca nô đi được trong \(2\) giờ \(30\) phút \(= 2 , 5\) giờ

Ta có \(s = 2 , 5. \left(\right. x + 6 \left.\right)\) (km).

Do \(x + 6 \leq 46\) nên \(2 , 5. \left(\right. x + 6 \left.\right) < 2 , 5.46\) hay \(s \leq 115\)

Vậy quãng đường ca nô đi được trong \(2\) giờ \(30\) phút không vượt quá \(115\) km.

a) Vẽ đường tròn \(\left(\right. C ; 2\) cm\(\left.\right)\)

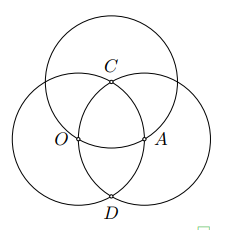
b) Đường tròn \(\left(\right. O ; 2\) cm\(\left.\right)\) và \(\left(\right. A ; 2\) cm\(\left.\right)\) cắt nhau tại \(C\), \(D\), điểm \(A\) nằm trên đường tròn tâm \(O\) nên:

\(O C = O D = 2\) cm, \(A C = A D = 2\) cm.

Suy ra \(O C = C A = 2\) cm.

Do đó đường tròn \(\left(\right. C ; 2\) cm\(\left.\right)\) đi qua hai điểm \(O\) và \(A\).

a) Xét tam giác \(A B H\) vuông tại \(H\), ta có \(H B = A H . tan ⁡ \hat{B A H} = 4. tan ⁡ 2 8^{\circ} \approx 2 , 1\) (cm)

Vì tam gaisc \(A H C\) vuông tại \(H\) nên \(H C = A H . cot ⁡ \hat{C} = 4. cot ⁡ 4 1^{\circ} \approx 4 , 6\) (cm)

b) Xét tam giác \(A B H\) vuông tại \(H\), ta có

\(cos ⁡ \hat{B A H} = \frac{A H}{A B}\) hay \(A B = \frac{A H}{cos ⁡ \hat{B A H}} = \frac{4}{cos ⁡ 28 ^{\circ}} \approx 4 , 5\) (cm)

Vì tam giác \(A H C\) vuông tại \(H\) nên \(sin ⁡ \hat{C} = \frac{A H}{A C}\) hay \(A C = \frac{A H}{sin ⁡ \hat{C}} = \frac{4}{sin ⁡ 4 1^{\circ}} \approx 6 , 1\) (cm).

Xét \(\Delta A B H\) vuông tại \(H\) có \(A H = A B . sin ⁡ \hat{B} = 3. sin ⁡ 6 0^{\circ} \approx 2 , 6\)

Tương tự, xét \(B H = A B . cos ⁡ \hat{B} = 3. cos ⁡ 6 0^{\circ} = 1 , 5\)

Mà \(H C = B C - H B = 4 , 5 - 1 , 5 = 3 , 0\)

Theo định lí Pythagore ta có \(A B^{2} = B H^{2} + A H^{2} = 3^{2} + 2 , 6^{2} = 15 , 76\)

Suy ra \(A B = \sqrt{15 , 76} \approx 4 , 0\)

Xét \(\Delta A H C\) vuông tại \(H\) ta có \(tan ⁡ \hat{A C H} = \frac{A H}{H C} \approx \frac{2 , 6}{3 , 0} \approx tan ⁡ 4 0^{\circ} 5 5^{'}\)

Do \(\hat{A} = 18 0^{\circ} - \hat{B} - \hat{C} = 18 0^{\circ} - \left(\right. 6 0^{\circ} + 4 0^{\circ} 5 5^{'} \left.\right) = 7 9^{\circ} 5^{'}\)

Xét \(\Delta \&\text{nbsp}; A B H\) vuông tại \(H\) có \(A H = A B . sin ⁡ \hat{B} = 2 , 1. sin ⁡ 7 0^{\circ} \approx 1 , 97\)

Tương tự, xét \(B H = A B . cos ⁡ \hat{B} = 2 , 1. cos ⁡ 7 0^{\circ} \approx 0 , 72\)

Mặt khác, xét \(\Delta A H C\) vuông tại \(H\) ta có

\(sin ⁡ \hat{C} = \frac{A H}{A C} \approx \frac{1 , 97}{3 , 8} \approx sin ⁡ 3 1^{\circ} 1 4^{'}\)

Do đó \(\hat{C} \approx 3 1^{\circ} 1 4^{'}\)

Mà \(\hat{A} = 18 0^{\circ} - \left(\right. 7 0^{\circ} + 3 1^{\circ} 1 4^{'} \left.\right) = 7 8^{\circ} 4 6^{'}\)

Ta có \(H C = A C . cos ⁡ \hat{C} \approx 3 , 80. cos ⁡ 3 1^{\circ} 1 4^{'} \approx 3 , 25\)

Mà \(B C = B H + H C = 0 , 72 + 3 , 25 = 3 , 97\).

Ta có \(\hat{A} = 180 ^{\circ} - \hat{B} - \hat{C} = 7 5^{\circ}\)

Kẻ đường cao \(B H\).

Xét \(\Delta B C H\) vuông tại \(H\), ta có:

\(B H = B C . sin ⁡ \hat{C} = 4 , 2. sin ⁡ 4 0^{\circ} \approx 2 , 70\) (cm)

Tương tự, xét \(\Delta A B H\) vuông tại \(H\), ta có:

\(A B = \frac{B H}{sin ⁡ \hat{A}} = \frac{2 , 70}{sin ⁡ 7 5^{\circ}} \approx 2 , 8\) (cm)

Mặt khác ta có \(A C = A H + C H = B H . \left(\right. cot ⁡ \hat{A} + cot ⁡ \hat{C} \left.\right) \&\text{nbsp}; \approx 2 , 70. \left(\right. cot ⁡ 7 5^{\circ} + cot ⁡ 4 0^{\circ} \left.\right) \approx 3 , 9\) cm.

Ta có \(\hat{A} = 18 0^{\circ} - \hat{B} - \hat{C} = 7 0^{\circ}\).

Kẻ đường cao \(A H\).

Xét \(\Delta A B H\) vuông tại \(H\), ta có \(A H = A B . sin ⁡ \hat{B} = 2 , 8. sin ⁡ 6 5^{\circ} \approx 2 , 54\) (cm).

Tương tự \(B H = A B . cos ⁡ \hat{B} = 2 , 8. cos ⁡ 6 5^{\circ} \approx 1 , 18\) (cm).

Mặt khác do giả thiết suy ra tam giác \(H A C\) vuông cân tại \(H\) nên \(H A = H C\).

Do đó \(B C \approx 2 , 54 + 1 , 18 = 3 , 7\) (cm).

Xét \(\Delta A H C\) vuông tại \(H\), ta có \(A C = \frac{H A}{sin ⁡ C} = \frac{2 , 54}{sin ⁡ 4 5^{\circ}} \approx 3 , 6\) (cm).

⚡Nếu \(x < 1\) thì \(x^{8} - x^{7} + x^{2} - x + 1\)

\(= x^{8} + x^{2} \left(\right. 1 - x^{5} \left.\right) + \left(\right. 1 - x \left.\right) > 0\).

⚡Nếu \(x \geq 1\) thì \(x^{8} - x^{7} + x^{2} - x + 1\)

\(= x^{7} \left(\right. x - 1 \left.\right) + x \left(\right. x - 1 \left.\right) + 1 > 0\).

Bất đẳng thức cần chứng minh tương đương với   \(2 \left(\right. \frac{a^{2}}{b^{2}} + \frac{b^{2}}{c^{2}} + \frac{c^{2}}{a^{2}} \left.\right) \geq 2 \left(\right. \frac{c}{b} + \frac{b}{a} + \frac{a}{c} \left.\right)\)

Xét dấu hiệu \(2 \left(\right. \frac{a^{2}}{b^{2}} + \frac{b^{2}}{c^{2}} + \frac{c^{2}}{a^{2}} \left.\right) - 2 \left(\right. \frac{c}{b} + \frac{b}{a} + \frac{a}{c} \left.\right)\)

\(= \left(\right. \frac{a}{b} - \frac{b}{c} \left.\right)^{2} + \left(\right. \frac{b}{c} - \frac{c}{a} \left.\right)^{2} + \left(\right. \frac{c}{a} - \frac{a}{b} \left.\right)^{2} \geq 0\)

Từ đó suy ra đpcm.