

NGUYỄN CÔNG THĂNG
Giới thiệu về bản thân



































a) Đa thức T biểu diễn tổng số tiền Bác Đô phải trả :
\(45000. x + 62000. y + 72000. z \left(\right. đ \overset{ˋ}{\hat{o}} n g \left.\right)\)
b) \(x = 1 , 5 ; y = 3 ; z = 2\)
Số tiền Bác Đô phải trả khi mua 1,5 kg vải; 3 kg cam; 2 kg nho là :
\(45000.1 , 5 + 62000.3 + 72000.2\)
\(= 67500 + 186000 + 144000\)
\(= 397500 \left(\right. đ \overset{ˋ}{\hat{o}} n g \left.\right)\)
VS.MNPQ=31.SMNPQ.SO
\(\Rightarrow S_{M N P Q} = \frac{3. V_{S . M N P Q}}{S O} = \frac{3.1280}{15} = 256 c m^{2}\)
Xét tg vuông SOI
\(O I = \sqrt{S I^{2} - S O^{2}}\) (Pitago)
\(\Rightarrow O I = \sqrt{1 7^{2} - 1 5^{2}} = 8 c m\)
Ta có
\(O I = \frac{M N}{2} \Rightarrow M N = 2. O I = 2.8 = 16 c m\)
a) Tứ giác ABCD có:
\(\hat{A} + \hat{B} + \hat{C} + \hat{D} = 36 0^{0}\) (tổng các góc trong tứ giác ABCD)
Gọi \(x , y , z , t\) lần lượt là số đo các góc: \(\hat{A} , \hat{B} , \hat{C} , \hat{D}\) \(\left(\right. x , y , z , t > 0 \left.\right)\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{1} = \frac{y}{2} = \frac{z}{3} = \frac{t}{4} = \frac{x + y + z + t}{1 + 2 + 3 + 4} = \frac{36 0^{0}}{10} = 3 6^{0}\)
\(\frac{y}{2} = 3 6^{0} \Rightarrow y = 2.3 6^{0} = 7 2^{0}\) (nhận)
Vậy \(\hat{B} = 7 2^{0}\)
b) Đường chéo của màn hình điện thoại:
\(\sqrt{7^{2} + 15 , 5^{2}} \simeq 17 \left(\right. c m \left.\right)\) \(\simeq 17.2 , 54 \simeq 43 \left(\right. i n c h \left.\right)\)
a,10x2(2x−y)+6xy(y−2x)
\(= \&\text{nbsp}; 10 x^{2} \left(\right. 2 x - y \left.\right) - 6 x y \left(\right. 2 x - y \left.\right)\)
\(= \left(\right. 2 x - y \left.\right) \left(\right. 10 x^{2} - 6 x y \left.\right)\)
\(= 2 x \left(\right. 2 x - y \left.\right) \left(\right. 5 x - 3 y \left.\right)\)
\(b , x^{2} - 2 x + 1 - y^{2}\)
\(= \left(\right. x^{2} - 2 x + 1 \left.\right) - y^{2}\)
\(= \left(\right. x - 1 \left.\right)^{2} - y^{2}\)
\(= \left(\right. x - 1 - y \left.\right) \left(\right. x - 1 + y \left.\right)\)
a/
\(A = \frac{x + 15}{\left(\right. x - 3 \left.\right) \left(\right. x + 3 \left.\right)} + \frac{2}{x + 3} =\)
\(= \frac{x + 15 + 2 \left(\right. x - 3 \left.\right)}{\left(\right. x - 3 \left.\right) \left(\right. x + 3 \left.\right)} = \frac{3 x + 9}{\left(\right. x - 3 \left.\right) \left(\right. x + 3 \left.\right)} = \frac{3}{x - 3}\)
b/
\(\frac{3}{x - 3} = - \frac{1}{2} \Rightarrow x = x = - 3\)
c/
Để A nguyên
⇒x−3={−3;−1;1;3}
⇒x={0;−2;4;6}
A=5+2xy+14y−x2−5y2−2x
\(A = - x^{2} + 2 x y - 2 x - y^{2} + 2 y - 1 - 4 y^{2} + 12 y - 9 + 15\)
\(A = - \left[\right. x^{2} - 2 x \left(\right. y - 1 \left.\right) + \left(\left(\right. y - 1 \left.\right)\right)^{2} \left]\right. - \left(\left(\right. 2 y - 3 \left.\right)\right)^{2} + 15\)
\(A = - \left(\left(\right. x - y + 1 \left.\right)\right)^{2} - \left(\left(\right. 2 y - 3 \left.\right)\right)^{2} + 15\)
Mà: \(\left{\right. - \left(\left(\right. x - y + 1 \left.\right)\right)^{2} \leq 0 \\ - \left(\left(\right. 2 y - 3 \left.\right)\right)^{2} \leq 0 \Rightarrow A = - \left(\left(\right. x - y + 1 \left.\right)\right)^{2} - \left(\left(\right. 2 y - 3 \left.\right)\right)^{2} + 15 \leq 15\)
Dấu "=" xảy ra khi:
\(y = \frac{3}{2} ; x = \frac{1}{2}\)
Vậy: \(A_{m i n} = 15 \Leftrightarrow \left{\right. x = \frac{1}{2} \\ y = \frac{3}{2}\)
a)
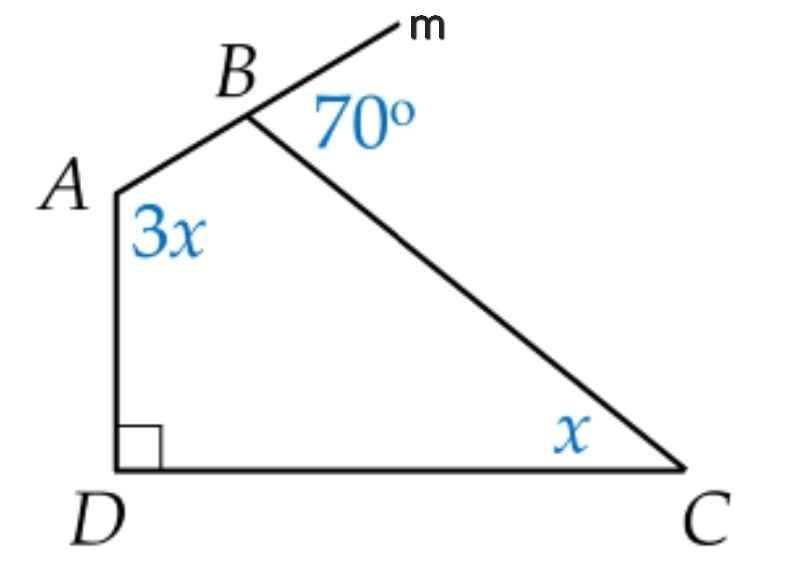 Ta có:
Ta có:
∠ABC + ∠CBm = 180⁰ (kề bù)
⇒ ∠ABC = 180⁰ - ∠CBm
= 180⁰ - 70⁰
= 110⁰
Tứ giác ABCD có:
∠A + ∠ABC + ∠C + ∠D = 360⁰ (tổng bốn góc trong tứ giác ABCD)
⇒ 3x + 110⁰ + x + 90⁰ = 360⁰
⇒ 4x + 200⁰ = 360⁰
⇒ 4x = 360⁰ - 200⁰
4x = 160⁰
⇒ x = 160⁰ : 4
⇒ x = 40⁰
b) ∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 3,7² - 1,2²
= 12,25
⇒ AH = 3,5
⇒ AH/BH = 3,5/1,2 ≈ 2,9 > 2,2
Vậy thang cách chân tường không "an toàn"
Thể tích của khúc gỗ là: 30.30.30 = 27 000 (cm3)
Thể tích của hình chóp từ giác đều là: 30.30.30.1/3 = 9 000 (cm3)
Thể tích của phần gỗ bị cắt đi là: 27 000 - 9 000 = 18 000 (cm3)
a) \(x^{2} - 2 x + 1 - y^{2}\)
\(= \left(\left(\right. x - 1 \left.\right)\right)^{2} - y^{2}\)
\(= \left(\right. x - y - 1 \left.\right) \left(\right. x + y - 1 \left.\right)\)
b) \(x^{2} - 8 x + 12\)
\(= x^{2} - 8 x + 16 - 4\)
\(= \left(\left(\right. x - 4 \left.\right)\right)^{2} - 2^{2}\)
\(= \left(\right. x - 4 - 2 \left.\right) \left(\right. x - 4 + 2 \left.\right)\)
\(= \left(\right. x - 6 \left.\right) \left(\right. x - 2 \left.\right)\)
Đúng(2) KV Kiều Vũ Linh 19 tháng 10 2023a) x² - 2x + 1 - y²
= (x² - 2x + 1) - y²
= (x - 1)² - y²)
= (x + y - 1)(x - y - 1)
b) x² - 8x + 12
= x² - 6x - 2x + 12
= (x² - 6x) - (2x - 12)
= x(x - 6) - 2(x - 6)
= (x - 6)(x - 2)
\(b , A = \frac{x^{2}}{x^{2} - 4} - \frac{x}{x - 2} - \frac{2}{x + 2} = \frac{x^{2}}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} - \frac{x}{x - 2} - \frac{2}{x + 2} = \frac{x^{2} - x \left(\right. x + 2 \left.\right) - 2 \left(\right. x - 2 \left.\right)}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} = \frac{x^{2} - x^{2} - 2 x - 2 x + 4}{\left(\right. x - 2 \left.\right) \left(\right. x + 2 \left.\right)} = \frac{- 4 x + 4}{x - 4}\)
`c,` Để `A=2` ta có
\(\frac{- 4 x + 4}{x - 4} = 2 \left(\right. x \neq 4 \left.\right) \Leftrightarrow \frac{- 4 x + 4}{x - 4} = \frac{2 \left(\right. x - 4 \left.\right)}{x - 4} \Leftrightarrow - 4 x + 5 = 2 x - 8 \Leftrightarrow - 6 x = - 13 \Leftrightarrow x = \frac{13}{6}\)