Theo em, bố bạn H đang có hành vi bạo lực về thể chất với bạn H khi bắt bạn làm việc quá 8 tiếng/ngày ở quán ăn để kiếm tiền, đây là việc quá sức với một đứa trẻ mới 15 tuổi - cái tuổi đáng ra bạn H phải được vui chơi, được học hành và được phát triển lành mạnh như các bạn đồng trang lứa. Và trong trường hợp này, bạn H nên ứng phó như sau: Nhờ sự trợ giúp của thầy cô, của bạn bè, của mọi người xung quanh ngay; phải nói với họ về tình trạng của bản thân để nhận được sự giúp đỡ kịp thời. Hoặc bạn có thể gọi đến số khẩn của Tổng đài Bảo vệ trẻ em 111 để nhận được sự tư vấn và giúp đỡ, tuyệt đối không được giấu giếm để tránh bị mất đi quyền học tập, phát triển vốn có và cũng tránh những trường hợp xấu có thể xảy ra.

Nếu là bạn, em sẽ khuyên H nên lập kế hoạch chi tiêu rõ ràng để kiểm soát chi tiêu của mình và có thể quản lí tài chính của bản thân tốt hơn. Phải có kế hoạch rõ ràng thì mới xác định được bản thân đang chi tiêu chưa hợp lí ở đâu để sửa đổi, phải lập kế hoạch chi tiêu để biết bản thân cần chi tiêu những gì, mua gì thực sự cần thiết để tránh tiêu xài hoang phí, có kế hạch chi tiêu rõ ràng thì phải tuân thủ theo, duy trì thực hiện để cải thiện thói quen chi tiêu chưa hợp lí.

Xét tam giác $ABC$, áo dụng tính chất tia phân giác trong tam giác, ta có: 

AMMB=ACCB=ABCB=ANNC(=ba)MBAM​=CBAC​=CBAB​=NCAN​(=ab​)

Vậy $MN$ // $BC$ (Định lí đảo của định lí Thalès)

Suy ra MNBC=AMAB=bb+aBCMN​=ABAM​=b+ab​ (Định lí Thalès)

Vậy nên MN=aba+b.MN=a+bab​.

​a) Xét tam giác $ABC$, áp dụng tính chất tia phân giác ta có:

ADDB=ACCB=126=2DBAD​=CBAC​=612​=2

Suy ra ADAB=23ABAD​=32​ suy ra AD=23.12=8AD=32​.12=8 (cm)

Do đó, $DB=12-8=4$ (cm).

b) Do $CE$ vuông góc với phân giác $CD$ nên $CE$ là phân giác ngoài tại đỉnh $C$ của tam giác $ABC$.

Vậy EBEA=BCACEAEB​=ACBC​ hay EBEB+BA=BCACEB+BAEB​=ACBC​

Gọi độ dài $EB$ là $x$ thì xx+12=612x+12x​=126​.

Vậy $x=12$ (cm).

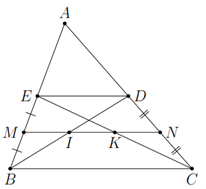
Xét $\Delta BED$ có {MI//EDME=BM{​MI//EDME=BM​ suy ra $ID=IB$.

Xét $\Delta CED$ có {NK//EDNC=ND{​NK//EDNC=ND​ suy ra $KE=KC$.

Suy ra MI=12EDMI=21​ED; NK=12EDNK=21​ED; ED=12BCED=21​BC.

IK=MK−MI=12BC−12DE=DE−12DE=12DEIK=MK−MI=21​BC−21​DE=DE−21​DE=21​DE.

Vậy $MI=IK=KN$.

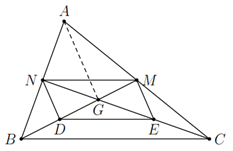
a) Vì $BM$, $CN$ là các đường trung tuyến của $\Delta ABC$ nên $MA=MC$, $NA=NB$.

Do đó $MN$ là đường trung bình của $\Delta ABC$, suy ra $MN$ // $BC$. (1)

Ta có $DE$ là đường trung bình của $\Delta GBC$ nên $DE$ // $BC$.  (2)

Từ (1) và (2) suy ra $MN$ // $DE$.

b) Xét $\Delta ABG$, ta có $ND$ là đường trung bình.

Xét $\Delta ACG$, ta có $ME$ là đường trung bình.

Do đó $ND$ // $AG$, $ME$ // $AG$.

Suy ra $ND$ // $ME$.

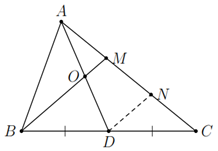
a) Qua $D$ vẽ một đường thẳng song song với $BM$ cắt $AC$ tại $N$.

Xét $\Delta MBC$ có $DB=DC$ và $DN$ // $BM$ nên MN=NC=12MCMN=NC=21​MC (định lí đường trung bình của tam giác).

Mặt khác AM=12MCAM=21​MC, do đó AM=MN=12MCAM=MN=21​MC.

Xét $\Delta AND$ có $AM=MN$ và $BM$ // $DN$ nên $OA=OD$ hay $O$ là trung điểm của $AD$.

b) Xét $\Delta AND$ có $OM$ là đường trung bình nên OM=12DNOM=21​DN. (1)

Xét $\Delta MBC$ có $DN$ là đường trung bình nên DN=12BMDN=21​BM. (2)

Từ (1) và (2) suy ra OM=14BMOM=41​BM.

a) Kẻ $MN$ // $BD$, $N\in AC$.

$MN$ là đường trung bình trong $△CBD$

Suy ra $N$ là trung điểm của $CD$ (1).

$IN$ là đường trung bình trong $△AMN$

Suy ra $D$ là trung điểm của $AN$ (2).

Từ (1) và (2) suy ra AD=12DCAD=21​DC.

b) Có ID=12MNID=21​MN; MN=12BDMN=21​BD, nên $BD=ID$.

Xét Tam giác ADB:  MN // AB (gt)

Suy ra:  DN/DB = MN/AB  (Hệ quả định lí Talét) (1)

Xét Tam giác ACB:  PQ // AB (gt)

Suy ra:  CQ/CB = PQ/AB    (Hệ quá định lí Talét)  (2)

Ta có:   NQ  sog sog  AB (gt)

             AB  sog sog  CD (gt)

Suy ra:  NQ  sog sog  CD (cùng sog sog  AB)

Xét Tam giác BDC:  NQ  sog sog  CD (cmt)

Suy ra:  DN/DB = CQ/CB (Định lí Talét)                (3)

Từ (1), (2) và (3)  suy ra:  MN/AB  =  PQ/AB

                             Suy ra:  MN = PQ  (đpcm).