

ĐẶNG XUÂN MINH
Giới thiệu về bản thân



































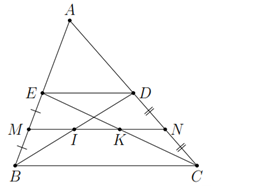
Do BD là đường trung tuyến của ∆ABC (gt)
⇒ D là trung điểm của AC
Do CE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AB
⇒ DE là đường trung bình của ∆ABC
⇒ DE // BC và DE = BC : 2
⇒ BC = 2DE
Do DE // BC (cmt)
⇒ BCDE là hình thang
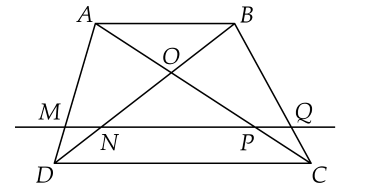
Do M là trung điểm của BE (gt)
N là trung điểm của CD (gt)
⇒ MN là đường trung bình của hình thang BCDE
⇒ MN // DE // BC và MN = (DE + BC) : 2
Do MN // DE (cmt)
⇒ MI // DE và NK // DE
∆BDE có:
MI // DE (cmt)
M là trung điểm của BE (gt)
⇒ I là trung điểm của BD
⇒ MI là đường trung bình của ∆BDE
⇒ MI = DE : 2 (1)
∆CDE có:
NK // DE (cmt)
N là trung điểm của CD (gt)
⇒ K là trung điểm của CE
⇒ NK là đường trung bình của ∆CDE
⇒ NK = DE : 2 (2)
Mà MI = DE : 2
⇒ MI = NK = DE : 2
⇒ MI + NK = DE
Ta có:
MN = (DE + BC) : 2
Mà BC = 2DE (cmt)
⇒ MN = (DE + 2DE) : 2
= DE + DE : 2
Lại có:
MN = MI + IK + NK
= (MI + NK) + IK
= DE + IK
⇒ DE + IK = DE + DE : 2
⇒ IK = DE : 2 (3)
Từ (1), (2) và (3) ⇒ MI = IK = KN
a/
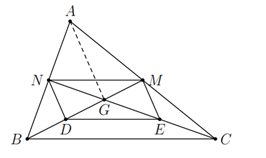
Xét tg ABC có
NA=NB; MA=MC => MN là đường trung bình của tg ABC => MN//BC
Xét tg GBC có
DG=DB; EG=EC => DE là đường trung bình của tg GBC => DE//BC
=> MN//DE (cùng // BC)
b/
Xét tg ABG có
NA=NB; DG=DB => ND là đường trung bình của tg ABG => ND//AG
Xét tg ACG có
MA=MC; EG=EC => ME là đường trung bình của tg ACG => ME//AG
=> ND//ME (cùng // với AG)
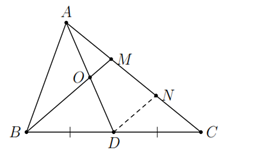
a/ Goi E là trung điểm của MC
Từ gt AM=12MC⇒AM=ME=ECAM=21MC⇒AM=ME=EC
Xét tg BCM có
ME=EC (cmt); DB=DC (gt) => DE là đường trung bình của tg BCM
=> DE//BM
Xét tg ADE có
AM=ME (cmt)
BM//DE (cmt) =>OM//DE
=> OA=OD (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
b/
Ta có DE là đường trung bình của tg BCM ⇒DE=12BM⇒DE=21BM
Xét tg ADE có
OA=OD (cmt); AM=ME (cmt) => OM là đường trung bình của tg ADE
⇒OM=12DE=12.12BM=14BM⇒OM=21DE=21.21BM=41BM
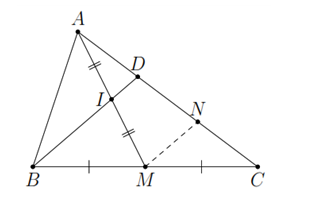
Gọi K là trung điểm của CD
a: Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của CD
Do đó: MK là đường trung bình
=>MK//BD
hay ID//MK
Xét ΔAMK có
I là trung điểm của AM
ID//MK
Do đó: D là trung điểm của AK
=>AD=DK=KC
=>AD=1/2DC
b: Xét ΔAMK có
I là trung điểm của AM
D là trung điểm của AK
Do đó: ID là đường trung bình
=>ID=MK/2
hay MK=2ID
Ta có: MK là đường trung bình của ΔBDC
nên MK=BD/2
=>BD/2=2ID
hay BD=4ID



Lấy D là trung điểm của cạnh BC.
Khi đó, AD là đường trung tuyến của tam giác ABC.
Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.
Ta có AGAD=23ADAG=32 hay AG=23ADAG=32AD
Vì MG // AB, theo định lí Thalès, ta suy ra: AGAD=BMBD=23ADAG=BDBM=32
Ta có BD = CD (vì D là trung điểm của cạnh BC) nên BMBC=BM2BD=22.3=13BCBM=2BDBM=2.32=31
Do đó BM=13BCBM=31BC (đpcm).
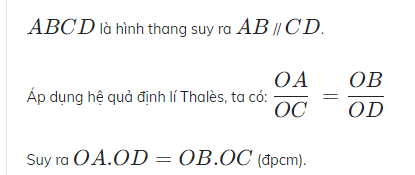
xét △ABC△ABC có:
@ED////AC=>[AE]/[AB]=[DC]/[BC]ED////AC=>AE/AB=DC/BC
@DF////AB=>[AF]/[AC]=[BD]/[BC]DF////AB=>AF/AC]=BD/BC
=>[AE]/[AB]+[AF]/[AC]=[DC+BD]/[BC]=[BC]/[BC]=1=>AE/AB+AF/AC=DC+BD/BC=BC/BC=1 (đpcm)(đpcm).
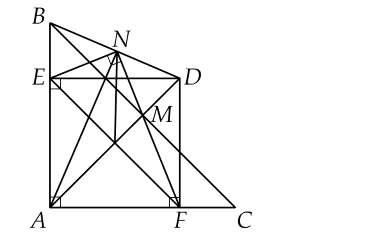
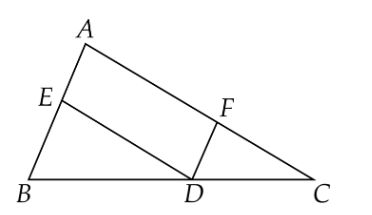
a) Chứng minh AEDF là hình vuông:
- Ta có: ΔABC vuông cân tại A (gt) => ∠BAC = 90 độ, AB = AC
- AE ⊥ AB, AF ⊥ AC (gt) => ∠AED = ∠AFD = 90 độ
- Tứ giác AEDF có 3 góc vuông nên AEDF là hình chữ nhật.
- Mà AD là đường chéo của hình chữ nhật AEDF (vì AD là đường trung trực của BC) => AEDF là hình vuông (hình chữ nhật có hai đường chéo bằng nhau).
b) Chứng minh EF // BC:
- Ta có: AEDF là hình vuông (cmt) => EF // AD (tính chất hình vuông)
- Mà AD // BC (do AM là đường trung bình của ΔABC) => EF // BC.
c) Chứng minh góc AND = 90 độ:
- Kẻ đường thẳng qua M vuông góc với EF cắt EF tại H.
- Ta có: MH ⊥ EF, AD ⊥ EF (vì AEDF là hình vuông) => MH // AD
- Mà M là trung điểm của BC => H là trung điểm của EF (đường trung bình của tam giác)
- Xét ΔMEF có:
- MH là đường trung trực của EF (vì MH ⊥ EF tại trung điểm H)
- EN ⊥ MF (gt) => AN là đường trung trực của MF (tính chất ba đường vuông góc) => AN ⊥ MF
- Mà MH // AD => AN ⊥ AD => Góc AND = 90 độ.