ABCD a) Do \(A B C D\) là hình bình hành nên \(A D\) // \(B C\) và \(A D = B C\).

Do \(A D\) // \(B C\) nên \(\hat{A D B} \&\text{nbsp}; = \hat{C B D}\) (so le trong)

Xét \(\Delta A D H\) và \(\Delta C B K\) có:

     \(\hat{A H D} \&\text{nbsp}; = \hat{C K B} = 9 0^{\circ}\);

     \(A D = B C\) (chứng minh trên);

     \(\hat{A D H} \&\text{nbsp}; = \hat{C B K}\) (do \(\hat{A D B} \&\text{nbsp}; = \hat{C B D}\)).

Do đó \(\Delta \&\text{nbsp}; A D H = \Delta \&\text{nbsp}; C B K\) (cạnh huyền – góc nhọn).

Suy ra \(A H = C K\) (hai cạnh tương ứng).

Ta có \(A H \bot \&\text{nbsp}; D B\) và \(C K \bot \&\text{nbsp}; D B\) nên \(A H\) // \(C K\).

Tứ giác \(A H C K\) có \(A H\) // \(C K\) và \(A H = C K\) nên \(A H C K\) là hình bình hành (dấu hiệu nhận biết).

b) Do \(A H C K\) là hình bình hành (câu a) nên hai đường chéo \(A C\) và \(H K\) cắt nhau tại trung điểm của mỗi đường.

Mà \(I\) là trung điểm của \(H K\) (giả thiết) nên \(I\) là trung điểm của \(A C\).

Do \(A B C D\) là hình bình hành nên hai đường chéo \(A C\) và \(B D\) cắt nhau tại trung điểm của mỗi đường.

Mà \(I\) là trung điểm của \(A C\) nên \(I\) là trung điểm của \(B D\), hay \(I B = I D\).

ABCD

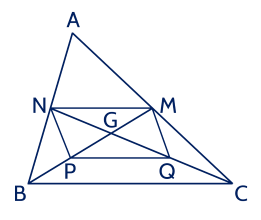
Xét tam giác \(A B C\) có hai đường trung tuyến \(B M\) và \(C N\) cắt nhau tại \(G\) (giả thiết) nên \(G\) là trọng tâm của \(\Delta A B C\).

Suy ra \(G M = \frac{G B}{2}\); \(G N = \frac{G C}{2}\) (tính chất trọng tâm của tam giác) (1)

Mà \(P\) là trung điểm của \(G B\) (giả thiết) nên \(G P = P B = \frac{G B}{2}\) (2)

\(Q\) là trung điểm của \(G C\) (giả thiết) nên \(G Q = Q C = \frac{G C}{2}\) (3)

Từ (1), (2) và (3) suy ra \(G M = G P\) và \(G N = G Q\).

Xét tứ giác \(P Q M N\) có: \(G M = G P\) và \(G N = G Q\) (chứng minh trên)

Do đó tứ giác \(P Q M N\) có hai đường chéo \(M P\) và \(N Q\) cắt nhau tại trung điểm \(G\) của mỗi đường nên là hình bình hành.

Xét tam giác \(A B C\) có hai đường trung tuyến \(B M\) và \(C N\) cắt nhau tại \(G\) (giả thiết) nên \(G\) là trọng tâm của \(\Delta A B C\).

Suy ra \(G M = \frac{G B}{2}\); \(G N = \frac{G C}{2}\) (tính chất trọng tâm của tam giác) (1)

Mà \(P\) là trung điểm của \(G B\) (giả thiết) nên \(G P = P B = \frac{G B}{2}\) (2)

\(Q\) là trung điểm của \(G C\) (giả thiết) nên \(G Q = Q C = \frac{G C}{2}\) (3)

Từ (1), (2) và (3) suy ra \(G M = G P\) và \(G N = G Q\).

Xét tứ giác \(P Q M N\) có: \(G M = G P\) và \(G N = G Q\) (chứng minh trên)

Do đó tứ giác \(P Q M N\) có hai đường chéo \(M P\) và \(N Q\) cắt nhau tại trung điểm \(G\) của mỗi đường nên là hình bình hành.

Xét tam giác \(A B C\) có hai đường trung tuyến \(B M\) và \(C N\) cắt nhau tại \(G\) (giả thiết) nên \(G\) là trọng tâm của \(\Delta A B C\).

Suy ra \(G M = \frac{G B}{2}\); \(G N = \frac{G C}{2}\) (tính chất trọng tâm của tam giác) (1)

Mà \(P\) là trung điểm của \(G B\) (giả thiết) nên \(G P = P B = \frac{G B}{2}\) (2)

\(Q\) là trung điểm của \(G C\) (giả thiết) nên \(G Q = Q C = \frac{G C}{2}\) (3)

Từ (1), (2) và (3) suy ra \(G M = G P\) và \(G N = G Q\).

Xét tứ giác \(P Q M N\) có: \(G M = G P\) và \(G N = G Q\) (chứng minh trên)

Do đó tứ giác \(P Q M N\) có hai đường chéo \(M P\) và \(N Q\) cắt nhau tại trung điểm \(G\) của mỗi đường nên là hình bình hành.

Xét tam giác \(A B C\) có hai đường trung tuyến \(B M\) và \(C N\) cắt nhau tại \(G\) (giả thiết) nên \(G\) là trọng tâm của \(\Delta A B C\).

Suy ra \(G M = \frac{G B}{2}\); \(G N = \frac{G C}{2}\) (tính chất trọng tâm của tam giác) (1)

Mà \(P\) là trung điểm của \(G B\) (giả thiết) nên \(G P = P B = \frac{G B}{2}\) (2)

\(Q\) là trung điểm của \(G C\) (giả thiết) nên \(G Q = Q C = \frac{G C}{2}\) (3)

Từ (1), (2) và (3) suy ra \(G M = G P\) và \(G N = G Q\).

Xét tứ giác \(P Q M N\) có: \(G M = G P\) và \(G N = G Q\) (chứng minh trên)

Do đó tứ giác \(P Q M N\) có hai đường chéo \(M P\) và \(N Q\) cắt nhau tại trung điểm \(G\) của mỗi đường nên là hình bình hành.

cộng tác viên, cộng tác viên hs , cộng tác viên vip hay sao á