

Đoàn Ngọc Hoàng Nghi
Giới thiệu về bản thân



































- Bác nông dân : Lúc đầu định giúp lừa ra khỏi giếng, nhưng sau nghĩ lừa già và cái giếng cũng cần được lắp. Vì thế, nhanh chóng buông xuôi, bỏ cuộc, quyết định lấp giếng.
- Con lừa : Lúc đầu kêu la thảm thiết muốn thoát khỏi giếng nhưng rồi đã khôn ngoan, dùng chính những xẻng đất muốn vùi lắp mình để tự cứu mình thoát ra khỏi cái giếng
- Học sinh đọc kĩ văn bản, trình bày bài học được rút ra từ văn bản hoặc các nhân vật
+ Coi trọng tình bạn
+ Cần cù, biết lo xa
+ ...
- Tình huống truyện: Xoay quanh chuyện làm nhà cũng như đi tìm kiếm thức ăn dự trữ cho mùa đông của Kiến và Ve Sầu
- Tình huống nhằm làm nổi bật tính cách lười biếng, không biết lo xa của Ve Sầu và tính cách chăm chỉ, biết suy nghĩ, lo xa và tiết kiệm của Kiến. Từ đó, làm nổi bật bài học đạo đức của văn bản
Câu 1. Thể loại: tuỳ bút.
Câu 2. “Nghệ thuật” ăn quà của người Hà Nội thể hiện qua việc “ăn đúng cái giờ ấy và chọn người bán ấy”, tức là chọn thời điểm ăn và chọn người bán món quà đúng mới thể hiện mình là người sành ăn. Đó chính là điều làm nên “nghệ thuật” ăn quà của người Hà Nội.
Câu 3.
– Biện pháp tu từ: so sánh.
– Tác dụng:
+ Gợi tả được hình ảnh con dao – dụng cụ hành nghề, vừa tái hiện được động tác đưa dao xắt miếng cơm một cách chuyên nghiệp, lành nghề của cô hàng cơm nắm.
+ Tăng tính sinh động, gợi hình cho câu văn.
Câu 4. Chủ đề của văn bản: miêu tả, ca ngợi cái hay, cái ngon của các thức quà Hà Nội.
Câu 5. HS nhận xét về cái tôi trữ tình của tác giả, có thể theo hướng: đó là cái tôi lãng mạn, trữ tình, am hiểu sâu sắc về ẩm thực Hà Nội,…
Câu 6.
HS trình bày được suy nghĩ của bản thân về sự gắn bó của mỗi người với quê hương, có thể theo hướng:
– Quê hương là nguồn cội, là những hình ảnh thân thuộc với mỗi người, cho nên việc gắn bó với quê hương là cần thiết.
– Sự gắn bó được thể hiện qua tình yêu, niềm tự hào về quê hương, góp sức xây dựng quê hương,…
Câu 9:
Hình ảnh so sánh:
Lúc con nằm ấm áp
Lời ru là tấm chăn
- Tác dụng:
+ Hình ảnh so sánh gợi lên niềm yêu thương và tấm lòng của người mẹ.
+ Tăng sức gợi hình, gợi cảm cho sự diễn đạt, tạo nên hình tượng thơ chân thật. Phải có một trái tim nhân hậu, giàu tình yêu thương với con tác giả mới phát hiện và ghi lại cảm xúc một cách chân thành và sâu sắc đến thế.
Câu 10:
Thông điệp chung từ các dòng thơ:
- Tình mẫu tử là vĩnh hằng, bất diệt, luôn tìm thấy bên cuộc đời mỗi người. Dẫu con lớn khôn, trưởng thành thì tình mẹ vẫn không xa vắng, vẫn ở bên con chia sẻ ngọt bùi, che chở đời con, dõi theo mỗi bước con đi, giúp con vững bước trên đường đời.
- Biết yêu thương mẹ, trân trọng và biết ơn tình cảm của mẹ dành cho mình.
- Học sinh rút ra được bài học cho bản thân : Thấu hiểu, đồng cảm, thương xót cho những người có hoàn cảnh khó khăn; đồng thời cần biết chủ động giúp đỡ, an ủi, động viên họ
- Biện pháp tu từ so sánh : xu vẫn tiếp tục đổ ra như mưa
- Tác động : Giups cho hình ảnh trong câu văn trở nên sinh động hơn ; đồng thời nhấn mạnh sự chia sẻ chia và tấm lòng nhân hậu, hào hiệp của các bạn học sinh trong trường dành cho cậu bé nạo ống khói đáng thương
a) Tổng số học sinh lớp 7A là : 15 + 20 + 10 + 5 = 50 (học sinh)
b) Tỉ lệ học sinh có học lực giỏi là : 15 : 50 = 30%
Tỉ lệ học sinh có học lực khá là : 20 : 50 = 40%
Tỉ lệ học sinh có học lực trung bình là : 10 : 50 = 20%
Tỉ lệ học sinh có học lực yếu là : 5 : 50 = 10%
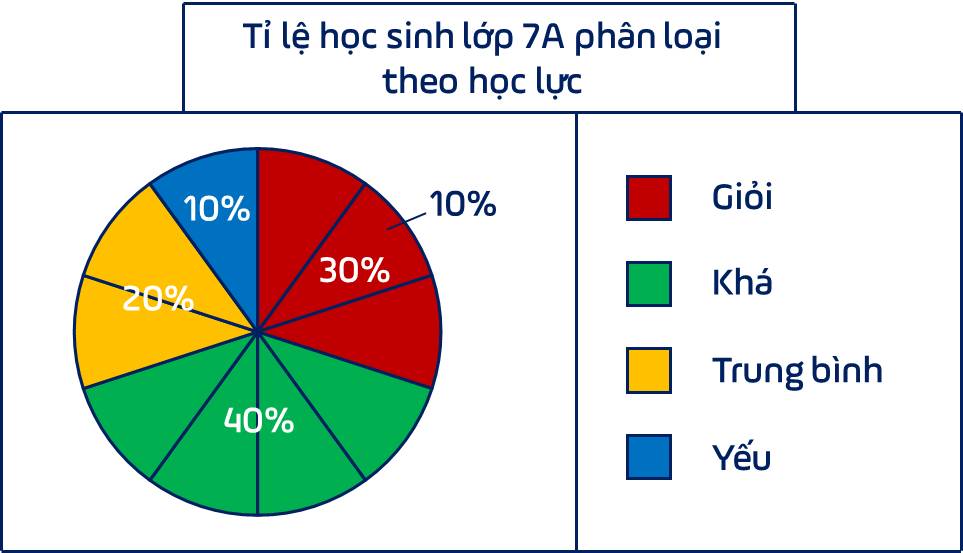
c) Hoàn thành biểu đồ hình quạt tròn:
Tiêu đề : Tỉ lệ học sinh lớp 7A phân loại theo học lực
a) \(\frac{x}{- 4} = \frac{- 11}{2}\)
\(x = \frac{\left(\right. - 11 \left.\right) . \left(\right. - 4 \left.\right)}{2}\)
\(x = 22\).
b) \(\frac{15 - x}{x + 9} \&\text{nbsp}; = \frac{3}{5}\)
\(\left(\right. 15 - x \left.\right) . 5 \&\text{nbsp}; = \left(\right. x + 9 \left.\right) . 3\)
\(75 - 5 x \&\text{nbsp}; = 3 x + 27\)
\(8 x = 48\)
\(x = 6\).
a) \(\hat{m O x} + \hat{x O n} = 18 0^{\circ}\) (hai góc kề bù)
Vậy \(\hat{n O x} = 18 0^{\circ} - 3 0^{\circ} = 15 0^{\circ}\).
\(O t\) là tia phân giác của \(\hat{n O x}\), suy ra \(\hat{n O t} = \frac{1}{2} . \hat{n O x} = 7 5^{\circ}\).
b) a // b suy ra \(\hat{A_{4}} = \hat{B_{2}} = 6 5^{\circ}\) (hai góc so le trong).
Mặt khác, ta có \(\hat{B_{2}} + \hat{B_{3}} = 18 0^{\circ}\) (hai góc kề bù)
Suy ra \(\hat{B_{3}} = 18 0^{\circ} - \hat{B_{2}} = 11 5^{\circ}\).