

Đào Khắc Sang
Giới thiệu về bản thân



































a) Xét △���△IOE và △���△IOF có
�^=�^=90∘E=F=90∘ (giả thiết);
��OI cạnh chung;
���^=���^EOI=FOI (��Om là tia phân giác).
Vậy △���=△���△IOE=△IOF (cạnh huyền - góc nhọn).
b) △���=△���△IOE=△IOF (chứng minh trên)
⇒��=��⇒OE=OF (hai cạnh tương ứng).
Gọi �H là giao điểm của ��Om và ��EF.
Xét △���△OHE và △���△OHF, có
��=��OE=OF (chứng minh trên);
���^=���^EOH=FOH (��Om là tia phân giác);
OHOH chung.
Do đó △���=△���△OHE=△OHF (c.g.c)
⇒���^=���^⇒OHE=FHO (hai góc tương ứng)
Mà ���^+���^=180∘OHE+FHO=180∘ nên ���^=���^=90∘OHE=FHO=90∘.
Vậy ��⊥��EF⊥Om.
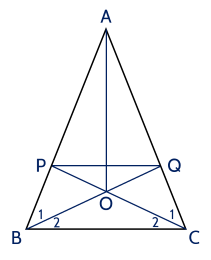
a) △���△ABC cân tại �A nên ���^=���^ABC=ACB.
Vì ��BQ và ��CP là đường phân giác của �^,�^B,C nên �1^=�2^=���^2B1=B2=2ABC, �1^=�2^=���^2C1=C2=2ACB.
Do đó �1^=�2^=�1^=�2^B1=B2=C1=C2.
Suy ra △���△OBC cân tại �O.
b) Vì �O là giao điểm các đường phân giác ��CP và ��BQ trong △���△ABC nên �O là giao điểm ba đường phân giác trong △���△ABC.
Do đó, �O cách đều ba cạnh ��,��AB,AC và ��BC.
c) Ta có △���△ABC cân tại �,��A,AO là đường phân giác của góc �A nên ��AO đồng thời là trung tuyến và đường cao của △���△ABC.
Vậy đường thẳng ��AO đi qua trung điểm của đoạn thẳng ��BC và vuông góc với nó.
d) Ta có △���=△���△PBC=△QCB (g.c.g)
⇒��=��⇒CP=BQ (hai cạnh tương ứng).
e) Ta có ��=��−��AP=AB−BP, ��=��−��AQ=AC−CQ (1);
△���=△���⇒��=��△PBC=△QCB⇒BP=CQ (2).
Lại có ��=��AB=AC (tam giác ���ABC cân tại �A) (3).
Từ (1), (2) và (3) suy ra ��=��AP=AQ.
Vậy tam giác ���APQ cân tại �A.

a) △���△ABC cân tại �A nên ���^=���^ABC=ACB.
Vì ��BQ và ��CP là đường phân giác của �^,�^B,C nên �1^=�2^=���^2B1=B2=2ABC, �1^=�2^=���^2C1=C2=2ACB.
Do đó �1^=�2^=�1^=�2^B1=B2=C1=C2.
Suy ra △���△OBC cân tại �O.
b) Vì �O là giao điểm các đường phân giác ��CP và ��BQ trong △���△ABC nên �O là giao điểm ba đường phân giác trong △���△ABC.
Do đó, �O cách đều ba cạnh ��,��AB,AC và ��BC.
c) Ta có △���△ABC cân tại �,��A,AO là đường phân giác của góc �A nên ��AO đồng thời là trung tuyến và đường cao của △���△ABC.
Vậy đường thẳng ��AO đi qua trung điểm của đoạn thẳng ��BC và vuông góc với nó.
d) Ta có △���=△���△PBC=△QCB (g.c.g)
⇒��=��⇒CP=BQ (hai cạnh tương ứng).
e) Ta có ��=��−��AP=AB−BP, ��=��−��AQ=AC−CQ (1);
△���=△���⇒��=��△PBC=△QCB⇒BP=CQ (2).
Lại có ��=��AB=AC (tam giác ���ABC cân tại �A) (3).
Từ (1), (2) và (3) suy ra ��=��AP=AQ.
Vậy tam giác ���APQ cân tại �A.
a) Xét △���△OAD và △���△OCB, có
��=��OA=OC (giả thiết);
�^O chung;
��=��OD=OB (giả thiết).
Do đó △���=△���△OAD=△OCB (c.g.c)
⇒��=��⇒AD=CB (hai cạnh tương ứng).
b) Do ��=��OA=OC và ��=��OB=OD nên ��=��AB=CD.
Mà △���=△���△OAD=△OCB (chứng minh trên)
⇒���^=���^⇒OBC=ODA; ���^=���^OAD=OCB (hai góc tương ứng)
Mặt khác ���^+���^=���^+���^=180∘ABE+OBC=CDE+ODA=180∘
⇒���^=���^⇒ABE=CDE
Xét △���△ABE và △���△CDE có
���^=���^OAD=OCB (chứng minh trên);
��=��AB=CD (chứng minh trên);
���^=���^ABE=CDE (chứng minh trên)
Do đó △���=△���△ABE=△CDE (g.c.g).
c) Vi △���=△���△ABE=△CDE (chứng minh trên) nên ��=��AE=CE (hai cạnh tương ứng).
Xét △���△AEO và △���△CEO có ��=��AE=CE (chứng minh trên);
��OE cạnh chung;
��=��OA=OC (giả thiết).
Do đó △���=△���△AEO=△CEO (c.c.c)
⇒���^=���^⇒AOE=COE (hai góc tương ứng)
⇒��⇒OE là tia phân giác của ���^xOy.

a) △���△ABC cân tại �A nên ���^=���^ABC=ACB.
Vì ��BQ và ��CP là đường phân giác của �^,�^B,C nên �1^=�2^=���^2B1=B2=2ABC, �1^=�2^=���^2C1=C2=2ACB.
Do đó �1^=�2^=�1^=�2^B1=B2=C1=C2.
Suy ra △���△OBC cân tại �O.
b) Vì �O là giao điểm các đường phân giác ��CP và ��BQ trong △���△ABC nên �O là giao điểm ba đường phân giác trong △���△ABC.
Do đó, �O cách đều ba cạnh ��,��AB,AC và ��BC.
c) Ta có △���△ABC cân tại �,��A,AO là đường phân giác của góc �A nên ��AO đồng thời là trung tuyến và đường cao của △���△ABC.
Vậy đường thẳng ��AO đi qua trung điểm của đoạn thẳng ��BC và vuông góc với nó.
d) Ta có △���=△���△PBC=△QCB (g.c.g)
⇒��=��⇒CP=BQ (hai cạnh tương ứng).
e) Ta có ��=��−��AP=AB−BP, ��=��−��AQ=AC−CQ (1);
△���=△���⇒��=��△PBC=△QCB⇒BP=CQ (2).
Lại có ��=��AB=AC (tam giác ���ABC cân tại �A) (3).
Từ (1), (2) và (3) suy ra ��=��AP=AQ.
Vậy tam giác ���APQ cân tại �A.
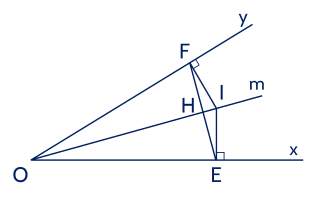
ho ���^xOy, (0∘<���^<180∘)(0∘<xOy<180∘), ��Om là tia phân giác ���^xOy. Trên tia ��Om lấy điểm �I bất kì. Gọi �,�E,F lần lượt là chân đường vuông góc kẻ từ �I đến ��Ox và ��Oy. Chứng minh:
a) △���=△���△IOE=△IOF.
b) ��⊥��EF⊥Om.
Hướng dẫn giải:

a) Xét △���△IOE và △���△IOF có
�^=�^=90∘E=F=90∘ (giả thiết);
��OI cạnh chung;
���^=���^EOI=FOI (��Om là tia phân giác).
Vậy △���=△���△IOE=△IOF (cạnh huyền - góc nhọn).
b) △���=△���△IOE=△IOF (chứng minh trên)
⇒��=��⇒OE=OF (hai cạnh tương ứng).
Gọi �H là giao điểm của ��Om và ��EF.
Xét △���△OHE và △���△OHF, có
��=��OE=OF (chứng minh trên);
���^=���^EOH=FOH (��Om là tia phân giác);
OHOH chung.
Do đó △���=△���△OHE=△OHF (c.g.c)
⇒���^=���^⇒OHE=FHO (hai góc tương ứng)
Mà ���^+���^=180∘OHE+FHO=180∘ nên ���^=���^=90∘OHE=FHO=90∘.
Vậy ��⊥��EF⊥Om.
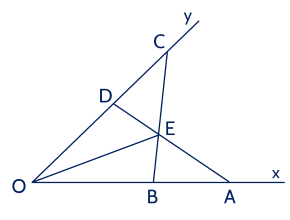
Cho ���^xOy. Lấy các điểm �,�A,B thuộc tia ��Ox sao cho ��>��OA>OB. Lấy các điểm �,�C,D thuộc ��Oy sao cho ��=��,��=��OC=OA,OD=OB. Gọi �E là giao điểm của ��AD và ��BC. Chứng minh rằng
a) ��=��AD=BC.
b) △���=△���△ABE=△CDE.
c) ��OE là tia phân giác của ���^xOy.
Kẻ ��⊥��IE⊥AD (với �∈��E∈AD).
Gọi ��Ax là tia đối của tia ��AB.
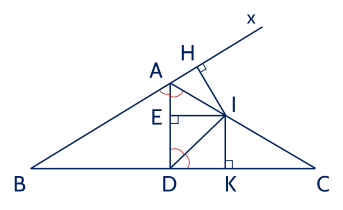
Vì ���^BAC và ���^CAx là hai góc kề bù mà ���^=120∘BAC=120∘ nên ���^=60∘CAx=60∘ (1)
Ta có ��AD là phân giác của ���^⇒���^=12���^=60∘BAC⇒DAC=21BAC=60∘ (2)
Từ (1) và (2) suy ra ��AC là tia phân giác của ���^DAx
⇒��=��⇒IH=IE (tính chất tia phân giác của một góc) (3)
Vì ��DI là phân giác của ���^ADC nên ��=��IK=IE (tính chất tia phân giác của một góc) (4)
Từ (3) và (4)(4) suy ra ��=��IH=IK.
Ta có �D thuộc phân giác của �^A;
��⊥��DH⊥AB; ��⊥��DK⊥AC ⇒��=��⇒DH=DK (tính chất tia phân giác của một góc).
Gọi �G là trung điểm của ��BC.
Xét △���△BGD và △���△CGD, có
���^=���^=90∘BGD=CGD=90∘ (��DG là trung trực của ��BC ),
��=��BG=CG (già thiết),
��DG là cạnh chung.
Do đó △���=△���△BGD=△CGD (hai cạnh góc vuông)
⇒��=��⇒BD=CD (hai cạnh tương ứng).
Xét △���△BHD và △���△CKD, có
���^=���^=90∘BHD=CKD=90∘ (giả thiết);
��=��DH=DK (chứng minh trên);
��=��BD=CD (chứng minh trên).
Do đó △���=△���△BHD=△CKD (cạnh huyền - cạnh góc vuông)
⇒��=��⇒BH=CK (hai cạnh t ứng).