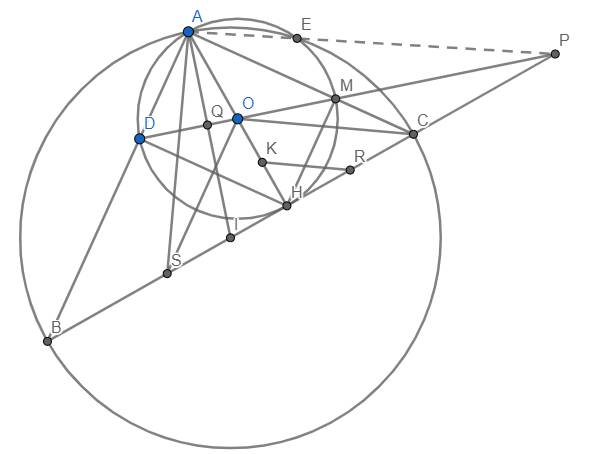
a) Chứng minh tam giác ABH vuông tại H và \(DH\perp AB\) rồi dùng hệ thức lượng \(\Rightarrow AD.AB=AH^2\). Tương tự, ta có \(AM.AC=AH^2\). Do đó \(AD.AB=AM.AC\) và theo bổ đề quen thuộc thì tứ giác BCMD nội tiếp. (đpcm)

b) Gọi Q là giao điểm của DM và AI. Khi đó tam giác ABC vuông tại A có trung tuyến AI nên \(IA=IB=IC=\dfrac{BC}{2}\) hay tam giác IBA cân tại I, suy ra \(\widehat{B}=\widehat{DAQ}\).

 Lại có \(\widehat{B}+\widehat{ACB}=90^o\) suy ra \(\widehat{DAQ}+\widehat{ADQ}=90^o\) (do \(\widehat{ADQ}=\widehat{ACB}\) (cmt)). Do đó \(PQ\perp AI\) tại Q. Từ đó dễ dàng chứng minh O là trực tâm tam giác AIP.

 c) Do tứ giác BCMD nội tiếp nên \(PM.PD=PC.PB\) \(\Rightarrow P_{P/\left(O\right)}=P_{P/\left(I\right)}\) \(\Rightarrow\) P nằm trên trục đẳng phương của (O) và (I). Lại có AE chính là trục đẳng phương của (O) và (I) nên A, E, P thẳng hàng. (đpcm)

 d) Ta thấy SO//AB \(\perp AC\) và \(AH\perp BC\) nên O là trực tâm tam giác ASC \(\Rightarrow OC\perp AS\)

 Lại có OC//KR nên \(RK\perp SA\) (đpcm)

Đề bài yêu cầu gì thế bạn?

 Mình nghĩ đây chắc chắn không phải toán 1 đâu nhưng mình vẫn giải bài này nhé:

 Đặt \(a=p_1^{k_1}p_2^{k_2}...p_n^{k_n}\) và \(b=p_1^{l_1}p_2^{l_2}...p_n^{l_n}\) (phân tích tiêu chuẩn của a và b)

 Khi đó \(a.b=p_1^{k_1+l_1}p_2^{k_2+l_2}...p_n^{k_n+l_n}\)

 Lại có \(\left(a;b\right)=p_1^{min\left\{k_1,l_1\right\}}p_2^{min\left\{k_2,l_2\right\}}...p_n^{min\left\{k_n,l_n\right\}}\)

 \(\left[a;b\right]=p_1^{max\left\{k_1,l_1\right\}}p_2^{max\left\{k_2,l_2\right\}}...p_n^{max\left\{k_n,l_n\right\}}\)

 Suy ra \(\left(a;b\right)\left[a;b\right]=p_1^{min\left\{k_1,l_1\right\}+max\left\{k_1,l_1\right\}}p_2^{min\left\{k_2,l_2\right\}+max\left\{k_2,l_2\right\}}...p_n^{min\left\{k_n,l_n\right\}+max\left\{k_n,l_n\right\}}\)

\(=p_1^{k_1+l_1}p_2^{k_2+l_2}...p_n^{k_n+l_n}\)

\(=ab\)

Vậy \(ab=\left(a;b\right).\left[a;b\right]\)

Do đó nếu \(ab=1293\) thì \(\left(a;b\right).\left[a;b\right]=1293\)

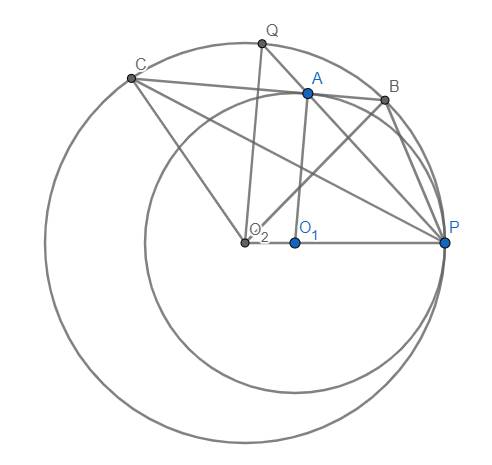
 Gọi Q là giao điểm của PA và (O₂). Do \(\widehat{O_1AP}=\widehat{O_1PA}=\widehat{O_2PQ}=\widehat{O_2QP}\) nên O₁A//O₂Q

 Mặt khác, \(BC\perp O_1A\) (vì BC là tiếp tuyến tại A của (O₁) nên \(BC\perp O_2Q\)

 \(\Rightarrow\) Q là điểm chính giữa của cung nhỏ BC 

 \(\Rightarrow\) PQ là tia phân giác \(\widehat{BPC}\) \(\Rightarrow\) đpcm

*Đoán nghiệm sử dụng tính chất của đa thức:

 Ta dễ dàng nhận thấy đa thức \(P\left(x\right)=x^3+4x^2-19x+24\) không có nghiệm là \(\pm1\).

 Giả sử \(P\left(x\right)\) có nghiệm hữu tỉ dạng \(\dfrac{p}{q}\left(p,q\inℤ\right)\), không mất tổng quát giả sử \(q>0\). Khi đó \(p|24\), \(q|1\) \(\Rightarrow q=1\).

 Khi đó do \(P\left(x\right)\) không có nghiệm là \(\pm1\) nên \(p\in\left\{\pm2,\pm3,\pm4;\pm6;\pm8;\pm12;\pm24\right\}\)

 Thử lại, ta thấy không có số \(p\) nào thỏa mãn \(\dfrac{p}{q}\) là nghiệm của P(x). Vậy đa thức \(P\left(x\right)\) không có nghiệm hữu tỉ \(\Rightarrow\) \(P\left(x\right)\) không thể phân tích thành nhân tử.

 * Chú ý rằng chỉ khi \(degP\left(x\right)\le3\) hoặc \(degP\left(x\right)⋮̸2\) thì từ P(x) không có nghiệm hữu tỉ mới suy ra được P(x) không phân tích được thành nhân tử nhé. Nếu \(\left\{{}\begin{matrix}degP\left(x\right)\ge4\\degP\left(x\right)⋮2\end{matrix}\right.\) thì chưa chắc điều này đã đúng. VD: Đa thức \(Q\left(x\right)=x^4+4\) không có nghiệm hữu tỉ (nó thậm chí còn không có nghiệm thực) nhưng ta vẫn có thể phân tích thành nhân tử như sau:

 \(Q\left(x\right)=x^4+4=x^4+4x^2+4-4x^2\)

\(=\left(x^2+2\right)^2-\left(2x\right)^2\)

\(=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\)

 Ta có \(a^n-a^{n-4}=a^{n-4}\left(a^4-1\right)=N\)

 Ta thấy vì \(a^{n-4}\) và \(a^4-1\) không cùng tính chẵn lẻ nên \(N⋮2\)

 Mặt khác, ta thấy nếu \(a⋮3\) thì hiển nhiên \(N⋮3\). Nếu \(a⋮̸3\) thì \(a^2\) chia 3 dư 1 (tính chất số chính phương), dẫn tới \(a^4=\left(a^2\right)^2\) chỉ có thể chia 3 dư 1 hay \(a^4-1⋮3\) với mọi \(a⋮̸3\). Vậy \(N⋮3\)

 Ta cần chứng minh \(N⋮5\).

 Dễ thấy điều này đúng nếu \(a⋮5\) 

 Với \(a⋮̸5\), khi đó \(a^2\) chia 5 dư 1 hoặc 4 (tính chất của số chính phương), suy ra \(a^4=\left(a^2\right)^2\) chia 5 chỉ có thể dư 1 (cũng là tính chất của số chính phương). Dẫn đến \(a^4-1⋮5\) với mọi \(a⋮̸5\). Vậy \(N⋮5\).

 Do đó \(N⋮2.3.5=30\) (đpcm)

Gọi 15 số đó là \(a_1,a_2,...,a_{15}\).

Ta chia 15 số này làm 3 nhóm:

\(\left(a_1,a_2,...,a_5\right);\left(a_6,a_7,...,a_{10}\right);\left(a_{11},a_{12},....,a_{15}\right)\)

Theo đề bài, có thể thấy:

\(a_1a_2...a_{15}< 0\), \(a_6a_7...a_{10}< 0\) và \(a_{11}a_{12}...a_{15}< 0\)

Do đó hiển nhiên \(a_1a_2...a_{15}< 0\) (tích của 3 số âm là 1 số âm)

 Nếu như theo kiến thức lớp 9 chưa học về đồ thị nào khác ngoài đồ thị bậc nhất (là 1 đường thẳng) thì 2 dạng bài này gần như tương đương nhau. Nhưng khi bạn lên cấp III và học những loại đồ thị đường cong bậc hai (ellipse, parabol, hyperbol, đường tròn,...) thì 2 dạng bài này rõ ràng khác xa nhau nhé. (Vì xác định hàm số thì đó có thể là hàm số kiểu gì cũng được, nhưng viết ptđt thì chỉ có liên quan đến đường thẳng thôi.)

1)

\(\dfrac{x-1}{2014}+\dfrac{x-2}{2013}+\dfrac{x-3}{2012}+...+\dfrac{x-2014}{1}=2014\)

\(\Leftrightarrow\left(\dfrac{x-1}{2014}-1\right)+\left(\dfrac{x-2}{2013}-1\right)+...+\left(\dfrac{x-2014}{1}-1\right)=0\)

\(\Leftrightarrow\dfrac{x-2015}{2014}+\dfrac{x-2015}{2013}+...+\dfrac{x-2015}{1}=0\)

\(\Leftrightarrow\left(x-2025\right)\left(\dfrac{1}{2014}+\dfrac{1}{2013}+...+\dfrac{1}{1}\right)=0\)

\(\Leftrightarrow x=2015\)

Vậy \(S=\left\{2015\right\}\)

 Đpcm \(\Leftrightarrow a^{b+4}-a^b⋮10\) \(\Leftrightarrow a^b\left(a^4-1\right)⋮10\), dễ thấy điều này đúng với \(a=5\).

 Nếu \(a⋮̸5\) thì \(a^2mod5\in\left\{1,4\right\}\) \(\Leftrightarrow a^4mod5\in\left\{1\right\}\) \(\Leftrightarrow a^4-1⋮5\) với mọi \(0< a< 10,a\ne5\). Vậy ta có \(a^b\left(a^4-1\right)⋮10\) với mọi \(0< a< 10\).

 Hơn nữa, do \(a^b\) và \(a^4-1\) không cùng tính chẵn lẻ nên \(a^b\left(a^4-1\right)⋮2\) với mọi \(0< a< 10\).

 Do vậy \(a^b\left(a^4-1\right)⋮10\) với mọi \(0< a< 10\), suy ra đpcm.